Article contents
On sigma-phi numbers
Published online by Cambridge University Press: 26 February 2010
Extract
Let
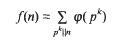
where φ denotes Euler's function. In this memoir we study the set w of sigmaphi numbers, that is, those composite natural numbers n which satisfy
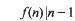
The smallest such number is 65, and they appear to be moderately frequent. There are 290 sigma-phi numbers not exceeding 105 and 1,231 not exceeding 106. By comparison, we observe that the number of primes in these ranges is 9,592 and 78,498, respectively. Since the primes also satisfy the relationship (1.2) a sigma-phi number can be thought of as a kind of pseudo-prime. The motivation for studying sigma-phi numbers is that they should have similar properties to Carmichael numbers but be easier to study. A Carmichael number is a number n such that the least common multiple of the φ(pk) with pk||n divides n-1, i.e., by Korseldt's criterion, a number for which p-1||n-1 whenever p|n. The number of Carmichael numbers not exceeding 105 and 106 is 16 and 43, respectively. It seems that the counting functions for Carmichael and sigma-phi numbers have somewhat similar growth rates. The counts above are skewed by the fact that there are many sigma-phi numbers with exactly two prime factors but there are no Carmichael numbers of this kind.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2001
References
- 3
- Cited by


