Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dobrovol'skii, N. M.
and
Van'kova, V. S.
1993.
On regular p-adic nets.
Mathematical Notes,
Vol. 54,
Issue. 6,
p.
1200.
Dobrovol'skii, N. M.
1995.
Means over orbits of multidimensional lattices.
Mathematical Notes,
Vol. 58,
Issue. 1,
p.
710.
Chen, W. W. L.
1996.
On irregularities of distribution III.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 60,
Issue. 2,
p.
228.
Chen, W.W.L
2000.
On Irregularities of Distribution IV.
Journal of Number Theory,
Vol. 80,
Issue. 1,
p.
44.
Montgomery, Hugh L.
2001.
Twentieth Century Harmonic Analysis — A Celebration.
p.
271.
Chen, W. W. L.
and
Skriganov, M.M.
2002.
Explicit constructions in the classical mean squares problem in irregularities of point distribution.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2002,
Issue. 545,
Temlyakov, V.N.
2003.
Cubature formulas, discrepancy, and nonlinear approximation.
Journal of Complexity,
Vol. 19,
Issue. 3,
p.
352.
Skriganov, M. M
2006.
Harmonic analysis on totally disconnected groups and irregularities of point distributions.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2006,
Issue. 600,
Chen, William W. L.
and
Skriganov, Maxim M.
2008.
Diophantine Approximation.
Vol. 16,
Issue. ,
p.
141.
SEKIYA, Nobuyasu
HIYAMA, Yukitaka
NAMIKI, Takao
KASAHARA, Yuji
CHINO, Atsushi
HAYASHI, Katsumi
KOGURE, Toshiaki
TATSUMI, Takeshi
SHIBAHARA, Naotoshi
KITA, Toshiaki
HIRASAKI, Yoshiro
and
TERASAWA, Katsutoshi
2008.
Consideration to Clinical Indication of Boiogito.
Kampo Medicine,
Vol. 59,
Issue. 4,
p.
623.
Bilyk, Dmitriy
Lacey, Michael T.
Parissis, Ioannis
and
Vagharshakyan, Armen
2009.
Exponential Squared Integrability of the Discrepancy Function in Two Dimensions.
Mathematika,
Vol. 55,
Issue. 1-2,
p.
1.
Hinrichs, Aicke
2010.
Discrepancy of Hammersley points in Besov spaces of dominating mixed smoothness.
Mathematische Nachrichten,
Vol. 283,
Issue. 3,
p.
478.
Triebel, Hans
2010.
Numerical integration and discrepancy, a new approach.
Mathematische Nachrichten,
Vol. 283,
Issue. 1,
p.
139.
Bilyk, Dmitriy
Temlyakov, V.N.
and
Yu, Rui
2012.
Fibonacci sets and symmetrization in discrepancy theory.
Journal of Complexity,
Vol. 28,
Issue. 1,
p.
18.
Chen, William W. L.
2012.
Monte Carlo and Quasi-Monte Carlo Methods 2010.
Vol. 23,
Issue. ,
p.
23.
Bilyk, Dmitriy
Temlyakov, Vladimir N.
and
Yu, Rui
2012.
Recent Advances in Harmonic Analysis and Applications.
Vol. 25,
Issue. ,
p.
63.
Markhasin, Lev
2013.
Quasi-Monte Carlo methods for integration of functions with dominating mixed smoothness in arbitrary dimension.
Journal of Complexity,
Vol. 29,
Issue. 5,
p.
370.
Hinrichs, Aicke
2013.
Monte Carlo and Quasi-Monte Carlo Methods 2012.
Vol. 65,
Issue. ,
p.
129.
Dick, Josef
2014.
Discrepancy bounds for infinite-dimensional order two digital sequences over F2.
Journal of Number Theory,
Vol. 136,
Issue. ,
p.
204.
Dick, Josef
and
Pillichshammer, Friedrich
2014.
A Panorama of Discrepancy Theory.
Vol. 2107,
Issue. ,
p.
539.


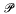 of
of 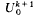 , where, for
, where, for 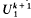 , let
, let 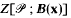 denote the number of points of
denote the number of points of 