Article contents
On Hayman's alternative
Published online by Cambridge University Press: 26 February 2010
Extract
Suppose that f(z) is non-constant and meromorphic in the plane and that, for some k≥= 1, a0(z),…, ak(z) are meromorphic in the plane with

for j' = 0,…, k. Here, using standard notation from [3], S(r,f) denotes any quantity satisfying S(r,f) = o(T(r,f)) as r→ ∞, possibly outside a set of finite linear measure. Then, setting
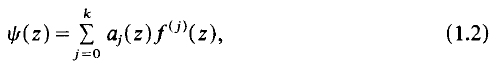
we have ([3, p. 57])
Theorem A. Suppose that f(z) is non-constant and meromorphic in the plane, and thatψ (z) given by (1.2) and (1.1) and is non-constant. Then
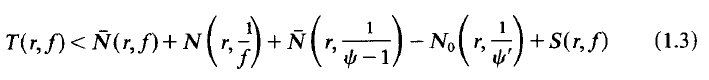
where N0(r, l/ψ') counts only zeros of ψ' which are not zeros of ψ − 1, and the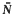 counting functions count points without regard to multiplicity.
counting functions count points without regard to multiplicity.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1985
References
- 4
- Cited by


