Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T16:50:03.161Z Has data issue: false hasContentIssue false
  • English
  • Français

On Construction of Saturated Distinguished Chains

Part of: Topological fields

Published online by Cambridge University Press:  21 December 2009

Amrit Pal Singh  and
Sudesh K. Khanduja
Amrit Pal Singh
Affiliation:
Department of Mathematics, Panjab University, Chandigarh-160014, India. E-mail: [email protected]
Sudesh K. Khanduja
Affiliation:
Department of Mathematics, Panjab University, Chandigarh-160014, India. E-mail: [email protected]
Get access

Abstract

Let υ be a Henselian valuation of arbitrary rank of a field K, and let ῡ be the (unique) extension of v to a fixed algebraic closure 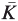of K. For an element α ∈ 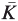\K, a chain α = α0, α1,…,αr of elements of 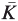, such that αi is of minimum degree over K with the property that ῡ(αi−1 − αi) = sup{ῡ(αi−1 − β) | [K (β) : K] < [K (αi−1) : K]} and that αr ∈ K, is called a saturated distinguished chain for α with respect to (K, υ). The notion of a saturated distinguished chain has been used to obtain results about the irreducible polynomials over any complete discrete rank one valued field K and to determine various arithmetic and metric invariants associated to elements of 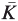(cf. [J. Number Theory, 52 (1995), 98–118.] and [J. Algebra, 266 (2003), 14–26]). In this paper, a method is described of constructing a saturated distinguished chain for α, and also determining explicitly some invariants associated to α, when the degree of the extension K (α)/K is not divisible by the characteristic of the residue field of υ.

MSC classification

Secondary: 12J10: Valued fields 12J25: Non-Archimedean valued fields
Type
Research Article
Information
Mathematika , Volume 54 , Issue 1-2 , December 2007 , pp. 59 - 65
Copyright
Copyright © University College London 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aghigh, K. and Khanduja, S. K., On the main invariant of elements algebraic over a henselian valued field. Proc. Edinburgh Math. Soc. 45 (2002), 219–227.CrossRefGoogle Scholar
2Aghigh, K. and Khanduja, S. K., On chains associated with elements algebraic over a henselian valued field. Algebra Colloquium 12:4 (2005), 607–616.CrossRefGoogle Scholar
3Endler, O., Valuation Theory. Springer-Verlag (1972).Google Scholar
4Khanduja, S. K., Popescu, N. and Roggenkamp, K. W., On minimal pairs and residually transcendental extensions of valuations. Mathematika 49 (2002), 93–106.Google Scholar
5Ota, K., On saturated distinguished chains over a local field. J. Number Theory 79 (1999), 217–248.Google Scholar
6Popescu, N. and Zaharescu, A., On the structure of the irreducible polynomials over local fields. J. Number Theory 52 (1995), 98–118.Google Scholar
7Popescu, A., Popescu, N. and Zaharescu, A., Metric invariants over Henselian valued fields. J. Algebra 266 (2003), 14–26.CrossRefGoogle Scholar