Article contents
On a problem of Barban and Vehov
Published online by Cambridge University Press: 26 February 2010
Extract
Barban and Vehov posed in [1] the problem of minimizing the quadratic form
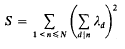
under the conditions
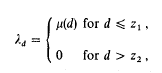
where 1 ≤ z1 < z2 and μ(n) is the Möbius function. They also commented on the connections of this problem with zero-density estimates of L-functions near the lines δ = 1 and ½, and with Linnik's prime number theorem. This program was carried out some years later by other authors, in the first place by Selberg [10], and later by Motohashi ([7]–[9]), Graham [2] and the present author ([4], [5]).
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1979
References
- 2
- Cited by


