Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T05:02:51.186Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on successive approximation

Published online by Cambridge University Press:  26 February 2010

D. D. Ang  and
D. E. Daykin
D. D. Ang
Affiliation:
University of Saigon, Saigon, Viet-Nam.
D. E. Daykin
Affiliation:
University of Malaya, Kuala Lumpur, Malaysia.
Get access

Extract

A well-known theorem of Schauder asserts that a continuous self-map T of a closed convex subset K of a normed linear space X, such that the closure 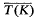of T(K) is compact, has at least one fixed point. No general method is known for a computation of the fixed point(s) of T.

Type
Research Article
Information
Mathematika , Volume 14 , Issue 1 , June 1967 , pp. 99 - 101
Copyright
Copyright © University College London 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Krasnoselski, M. A., “Two remarks on the method of successive approximation”, Uspehi Math. Nauk (N.S) 10, 63 (1955) (Russian) (quoted in [2]).Google Scholar
2.Bonsall, F. F., Lectures on some fixed points of functional analysis (Tata Institute of Fundamental Research, Bombay, 1962).Google Scholar
3.Edelstein, M., “A remark on a theorem of M. A. Krasnoselski”, Am. Math. Monthly, 73 (1966), No. 5.Google Scholar
4.Mann, W. R. and Blackburn, J. F., “A nonlinear steady state temperature problem”, Proc. Am. Math. Soc., 5 (1954).CrossRefGoogle Scholar
5.Ang, D. D. and Knopoff, L., A nonlinear temperature problem for the half-disk (Research Dept., IGP, Univ. Calif., L.A., 1965).Google Scholar
6.Edelstein, M., “On fixed and periodic points under a contractive mapping”, J. London Math. Soc., 37 (1962), 74–79.CrossRefGoogle Scholar