Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T05:32:15.498Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on linear transversely isotropic fluids

Published online by Cambridge University Press:  26 February 2010

A. E. Green
A. E. Green
Affiliation:
Department of Mathematics, The University of Newcastle upon Tyne
Get access

Extract

Green [8] has shown that a constitutive relation of the form

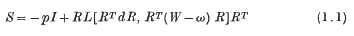
arises as a special case of an incompressible anisotropic simple fluid, where S is the stress tensor or matrix,

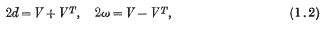
and V is the velocity gradient matrix at time t, all measured in a fixed rectangular cartesian coordinate system. Also, if F is the displacement gradient measured with respect to some curvilinear reference system θi, then

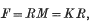
where R is a proper orthogonal matrix, and M and K are positive definite symmetric matrices. In addition

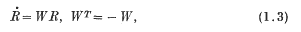
and

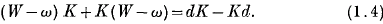
Type
Research Article
Information
Mathematika , Volume 12 , Issue 1 , June 1965 , pp. 27 - 29
Copyright
Copyright © University College London 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ericksen, J. L., Kolloid Zeitschrift, 173 (1960), 117.CrossRefGoogle Scholar
2. Ericksen, J. L., Arch. Rational Mech. Anal., 4 (1960), 231.CrossRefGoogle Scholar
3. Ericksen, J. L., Trans. Soc. Rheology, 4 (1960), 29.CrossRefGoogle Scholar
4. Ericksen, J. L., Arch. Rational Mech. Anal., 8 (1961), 1.CrossRefGoogle Scholar
5. Ericksen, J. L., Trans. Soc. Rheology, 5 (1961), 23.CrossRefGoogle Scholar
6. Ericksen, J. L., Trans. Soc. Rheology, 6 (1962), 273.CrossRefGoogle Scholar
7. Green, A. E., Proc. Camb. Phil. Soc, 60 (1964), 123CrossRefGoogle Scholar
8. Ericksen, J. L., Proc. Roy. Soc., A 279 (1964), 437.Google Scholar