Published online by Cambridge University Press: 26 February 2010
Let D(f) denote the discriminant of a binary cubic form
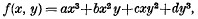
having integral coefficients. We restrict ourselves to forms with D(f) ≠ 0, and further (as a matter of convenience) to forms which are irreducible in the rational field. It is a problem of some interest, in connection with the approximation properties of transcendental numbers, to estimate the sum

as H→∞, where ‖f‖ = max(|a|, |b|, |c|, |d|). Since |D(f)| ≪ H4 when ‖f‖ < H, there is the trivial lower bound
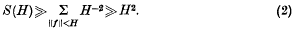
page 58 note † For an account of this connection, and the application of the result proved here, see the preceding paper by Professor Volkmann.
page 58 note ‡ J. London Math. Soc., 26 (1951), 183–192, 192–198Google Scholar.
page 59 note † See the first of the two papers cited.