Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T20:07:37.043Z Has data issue: false hasContentIssue false
  • English
  • Français

MONOCHROMATIC FACTORIZATIONS OF WORDS AND PERIODICITY

Part of: Discrete mathematics in relation to computer science Graph theory Extremal combinatorics

Published online by Cambridge University Press:  06 February 2018

Caïus Wojcik  and
Luca Q. Zamboni
Caïus Wojcik
Affiliation:
Institut Camille Jordan, Université Lyon 1, F69622 Villeurbanne, France email [email protected]
Luca Q. Zamboni
Affiliation:
Institut Camille Jordan, Université Lyon 1, F69622 Villeurbanne, France email [email protected]
Get access

Abstract

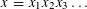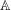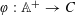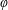In 2006 Brown asked the following question in the spirit of Ramsey theory: given a non-periodic infinite word $x=x_{1}x_{2}x_{3}\ldots$ with values in a set $\mathbb{A}$, does there exist a finite colouring $\unicode[STIX]{x1D711}:\mathbb{A}^{+}\rightarrow C$ relative to which $x$ does not admit a $\unicode[STIX]{x1D711}$-monochromatic factorization, i.e. a factorization of the form 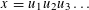$x=u_{1}u_{2}u_{3}\ldots$ with 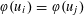$\unicode[STIX]{x1D711}(u_{i})=\unicode[STIX]{x1D711}(u_{\!j})$ for all 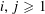$i,j\geqslant 1$? Various partial results in support of an affirmative answer to this question have appeared in the literature in recent years. In particular it is known that the question admits an affirmative answer for all non-uniformly recurrent words and for various classes of uniformly recurrent words including Sturmian words and fixed points of strongly recognizable primitive substitutions. In this paper we give a complete and optimal affirmative answer to this question by showing that if 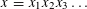$x=x_{1}x_{2}x_{3}\ldots$ is an infinite non-periodic word with values in a set 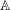$\mathbb{A}$, then there exists a 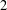$2$-colouring 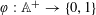$\unicode[STIX]{x1D711}:\mathbb{A}^{+}\rightarrow \{0,1\}$ such that for any factorization 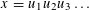$x=u_{1}u_{2}u_{3}\ldots$ we have 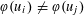$\unicode[STIX]{x1D711}(u_{i})\neq \unicode[STIX]{x1D711}(u_{\!j})$ for some 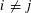$i\neq j$.

MSC classification

Primary: 68R15: Combinatorics on words 05C55: Generalized Ramsey theory 05D10: Ramsey theory
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 115 - 123
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avgustinovich, S. and Parshina, O., private communication.Google Scholar
Bernardino, A., Pacheco, R. and Silva, M., Coloring factors of substitutive infinite words. Discrete Math. 340 2017, 443–451.CrossRefGoogle Scholar
Brown, T. C., Colorings of the factors of a word. Preprint, 2006, Department of Mathematics, Simon Fraser University, Canada.Google Scholar
Durand, F., Host, B. and Skau, C., Substitutional dynamical systems, Bratteli diagrams and dimension groups. Ergodic Theory Dynam. Systems 19 1999, 953–993.Google Scholar
Hindman, N., Partitions and sums of integers with repetition. J. Combin. Theory Ser. A 27 1979, 19–32.Google Scholar
Hindman, N., Leader, I. and Strauss, D., Pairwise sums in colourings of the reals. Abh. Math. Semin. Univ. Hambg. (to appear).Google Scholar
Hindman, N. and Strauss, D., Algebra in the Stone–Čech Compactification: Theory and Applications, 2nd edn., de Gruyter (Berlin, 2012).Google Scholar
Leader, I., private communication.Google Scholar
de Luca, A., Pribavkina, E. and Zamboni, L. Q., A coloring problem for infinite words. J. Combin. Theory Ser. A 125 2014, 306–332.Google Scholar
de Luca, A. and Zamboni, L. Q., On some variations of coloring problems of infinite words. J. Combin. Theory Ser. A 137 2016, 166–178.Google Scholar
de Luca, A. and Zamboni, L. Q., On prefixal factorizations of words. European J. Combin. 52(part A) 2016, 59–73.CrossRefGoogle Scholar
Owings, J., Problem E2494. Amer. Math. Monthly 81 1974, 902.Google Scholar
Ramsey, F. P., On a problem of formal logic. Proc. Lond. Math. Soc. 30 1930, 264–286.Google Scholar
Salo, V. and Törmä, I., Factor colorings of linearly recurrent words. Preprint, 2015, arXiv:1504.0582.Google Scholar
Schützenberger, M. P., Quelques problèmes combinatoires de la théorie des automates, Cours professé à l’Institut de Programmation en 1966/67, notes by J.-F. Perrot, http://igm.univ-mlv.fr/∼berstel/Mps/Cours/PolyRouge.pdf.Google Scholar
Sierpiński, W., Sur un problème de la théorie des relations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 2 1933, 285–287.Google Scholar
Thue, A., Über unendliche Zeichenreihen. Skr. K. Nor. Vidensk. Selsk. 7 1906, 1–22.Google Scholar
Thue, A., Über die gegenseitige Lage gleicher Teile gewisser Zeichenreihen. Skr. K. Nor. Vidensk. Selsk. 1 1912, 1–67.Google Scholar
Zamboni, L. Q., A note on coloring factors of words, in Oberwolfach Report 37/2010, Mini-workshop: combinatorics on words, August 22–27, 2010, 42–44.Google Scholar