Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T04:50:35.626Z Has data issue: false hasContentIssue false
  • English
  • Français

Local inversion for differentiable functions and the Darboux property

Part of: Functions of several variables

Published online by Cambridge University Press:  26 February 2010

Jean Saint Raymond
Jean Saint Raymond
Affiliation:
Equipe d'Analyse—Boîte 186, Université Paris VI, 4, place Jussieu, F-75252 Paris CEDEX 05, France. E-mail: [email protected]
Get access

Abstract

The main goal of this paper is to prove that the classical theorem of local inversion for 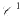functions extends in finite dimension to everywhere differentiable functions. As usual, a theorem of implicit functions can be deduced from this “Local Inversion Theorem”. The deepest part of the local inversion theorem consists of showing that a differentiable function with non-vanishing Jacobian determinant is locally one-to-one. In turn, this fact allows one to extend the Darboux property of derivative functions on ℝ (the range of the derivative is an interval) to the Jacobian function Df of a differentiable function, under the condition that this Jacobian function does not vanish. It is also proved that these results are no longer true in infinite dimension. These results should be known in whole or part, but references to a complete proof could not be found.

MSC classification

Secondary: 26B10: Implicit function theorems, Jacobians, transformations with several variables
Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 141 - 158
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Azagra, D. and Dobrowolski, T.. Smooth negligibility of compact sets in infinite-dimensional Banach spaces, with applications. Math. Annalen, 312 (1998), 445–463.CrossRefGoogle Scholar
2.Bessaga, C.. Every infinite-dimensional Hilbert space is diffeomorphic with its unit sphere. Bull. Acad Pol. Sci. Sér. Sci. Math. Astr. et Phys., 14 (1966), 27–31.Google Scholar
3.Cristea, M.. Some conditions for the local or global injectivity of a mapping between two nmanifolds. Rev. Roumaine Math. Pures Appl., 33 (1988), 861–869.Google Scholar
4.Cristea, M.. Local inversion theorems and implicit functions theorems without assuming differentiability. Bull. Math. Soc. Sci. Math. Roumanie (N.S.), 36 (1992). 227–236.Google Scholar
5.Martio, O., Rickman, S. and Väisälä, J.. Definitions for quasiregular mappings. Ann. Acad. Sci. Fenn. Ser. A I Math., 448 (1969), 1–40.Google Scholar
6.Rado, T. and Reichelderfer, P. V.. Continuous Transformations in Analysis. Springer Verlag (1955).CrossRefGoogle Scholar
7.Rudin, W.. Real and Complex Analysis (second edition). MacGraw-Hill Series in Higher Mathematics (1974).Google Scholar