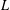 $L$-FUNCTIONS
$L$-FUNCTIONSPublished online by Cambridge University Press: 26 June 2018
We prove an exact formula for the second moment of Rankin–Selberg 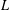 $L$-functions
$L$-functions 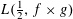 $L(\frac{1}{2},f\times g)$ twisted by
$L(\frac{1}{2},f\times g)$ twisted by 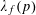 $\unicode[STIX]{x1D706}_{f}(p)$, where
$\unicode[STIX]{x1D706}_{f}(p)$, where 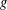 $g$ is a fixed holomorphic cusp form and
$g$ is a fixed holomorphic cusp form and 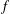 $f$ is summed over automorphic forms of a given level
$f$ is summed over automorphic forms of a given level 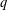 $q$. The formula is a reciprocity relation that exchanges the twist parameter
$q$. The formula is a reciprocity relation that exchanges the twist parameter 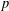 $p$ and the level
$p$ and the level 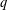 $q$. The method involves the Bruggeman–Kuznetsov trace formula on both ends; finally the reciprocity relation is established by an identity of sums of Kloosterman sums.
$q$. The method involves the Bruggeman–Kuznetsov trace formula on both ends; finally the reciprocity relation is established by an identity of sums of Kloosterman sums.
This material is based upon work supported by the National Science Foundation under Grant No. 1440140, while the authors were in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Spring semester of 2017. The first author is also supported by NSF grant DMS-1701638.