Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T15:18:04.495Z Has data issue: false hasContentIssue false
  • English
  • Français

Khinchin's conjecture and Marstrand's theorem

Published online by Cambridge University Press:  26 February 2010

R. C. Baker
R. C. Baker
Affiliation:
Royal Holloway College, Englefield Green, Surrey.
Get access

Extract

We begin by introducing some notations which will be used throughout the paper. Let 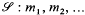denote a sequence of distinct positive integers. Let B denote a measurable subset of [0, 1) and {x} the fractional part of x. We write

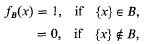
so that f has period 1 on the real line; and we write

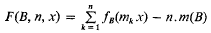
for the number of times {mkx} falls in B, minus the expected value of this number (m(B) ≤ Lebesgue measure of B).

Type
Research Article
Information
Mathematika , Volume 21 , Issue 2 , December 1974 , pp. 248 - 260
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, R. C.. “Discrepancy modulo one and capacity of sets”, Quart. J. Math. Oxford, (2), 22 (1971), 597–603.CrossRefGoogle Scholar
2.Baker, R. C.. “Some metrical theorems in strong uniform distribution”, to appear, Journ. Lond. Math. Soc.Google Scholar
3.Cassels, J. W. S.. “Some metrical theorems in diophantine approximation, III”, Proc. Camb. Phil. Soc, 46 (1950), 219–225.CrossRefGoogle Scholar
4.Edwards, R. E.. “Fourier series: a modern introduction, Vol. I” (Holt, Rinehart, Winston. New York 1967).Google Scholar
5.Erdos, P.. “On the strong law of large numbers”, Trans. Amer. Math. Soc., 67 (1949), 51–56.CrossRefGoogle Scholar
6.Erdos, P. and Koksma, J. F.. “On the uniform distribution modulo one of sequences (f(n, θ))”, Proc. Kon. Ned. Akad. v. Wet., 52 (1949), 851–854.Google Scholar
7.Erdos, P. and Taylor, S. J.. “On the set of points of convergence of a lacunary trigonometric series …”, Proc. Lond. Math. Soc., 7 (1957), 598–615.CrossRefGoogle Scholar
8.Kahane, J-P. and Salem, R.. “Ensembles parfaits et séries trigonometriques” (Hermann, Paris 1963).Google Scholar
9.Khinchin, A. Y.. “Ein Satz über Kettenbrüche mit arithmetischen Anwendungen”, Math. Zeit., 18 (1923), 289–306.CrossRefGoogle Scholar
10.Koksma, J. F.. “An arithmetical property of some summable functions”, Proc. Kon. Ned. Akad. v Wet., 53 (1950), 959–972.Google Scholar
11.Koksma, J. F.. “Estimation des fonctions a l'aide des integrates de Lebesgue”, Bull. Soc. Math. Belg., 6 (1953--4), 4–13.Google Scholar
12.Koksma, J. E.. “Sur les suites (λnx) et les fonctions g(t) ε L (2)”, Journ. de Math, pures et appl., 35 (1956), 289–296.Google Scholar
13.Marstrand, J. M.. “On Khinchin's conjecture about strong uniform distribution”, Proc. Lond. Math. Soc., 21 (1970), 540–556.CrossRefGoogle Scholar
14.Riesz, F.. “Sur la theorie ergodique”, Comment Math. Helv., 17 (1945), 221–239.CrossRefGoogle Scholar
15.Rogers, C. A.. “Hausdorff measures”, (Cambridge University Press, 1970).Google Scholar
16.Salem, R.. “Uniform distribution and capacity of sets”, Communications Sem. Math. Univ. Lund, supplement (1952), 193–195.Google Scholar
17.Weyl, H.. “Uber die Gleichverteilung von Zahlen mod. Eins”, Math. Annalen, 77 (1916), 313–352.CrossRefGoogle Scholar