Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T17:26:12.367Z Has data issue: false hasContentIssue false
  • English
  • Français

The integral cohomology ring of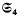

Published online by Cambridge University Press:  26 February 2010

C. B. Thomas
C. B. Thomas
Affiliation:
University College London
Get access

Extract

The cohomology of the symmetric groups with coefficients in a field has been studied by several authors, see [6] and [7] for example, but hardly anything has been published with the integers as coefficients. Given the connection between the infinite symmetric group and the classifying space BG for stable spherical fibrations, the computation of 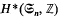is an interesting problem, and the purpose of this paper is to solve the first non-trivial case, n = 4. (The symmetric groups on 2 and 3 letters have cohomology of period four, which is generated by c1 and c2 of the permutation matrix representation, [8].)

Type
Research Article
Information
Mathematika , Volume 21 , Issue 2 , December 1974 , pp. 228 - 232
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Atiyah, M. F.. “Characters and cohomology of finite groups”, Publ. Math. IHES, 9, (1961), 23–64.CrossRefGoogle Scholar
2.Boorman, E.. “S-operations in representation theory”, Trans. Amer. Math. Soc. (to appear).Google Scholar
3.Cartan, H. and Eilenberg, S.. Homological Algebra (Princeton, 1956).Google Scholar
4.Evens, L.. “On the Chern classes of representations of finite groups”, Trans. Amer. Math. Soc, 115 (1965), 180–193.CrossRefGoogle Scholar
5.Hall, M. Jr. The Theory of Groups (Macmillan, New York, 1959).Google Scholar
6.Nakaoka, M.. “Note on cohomology algebras of symmetric groups”, Osaka City Univ. Jour. Math., 13 (1962), 45–55.Google Scholar
7.Quillen, D.. “The Adams Conjecture”, Topology, 10 (1971), 67–80.CrossRefGoogle Scholar
8.Thomas, C.. “Chern classes and groups with periodic cohomology”, Math. Annalen, 190 (1971), 323–328.CrossRefGoogle Scholar
9.Weiss, E.. “Kohomologiering und Darstellungsring endlicher Gruppen”, Bonner Math. Schriften, 36 (1969).Google Scholar