Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T23:45:30.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphically parameterized families of subgroups of sl(2, ℂ)

Part of: Other groups of matrices

Published online by Cambridge University Press:  26 February 2010

Robert Riley
Robert Riley
Affiliation:
SUNY-Binghamton, NY 13901 U.S.A.
Get access

Extract

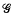Let be a finitely generated subgroup of SL (2, ℱ), where ℱ is the ring; of holomorphic functions on the open unit disc Δ. For each point z0 in Δ we can evaluate all matrix entries of 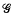at z0, to obtain a subgroup 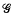{z0} of SL (2, ℂ) and a surjective representation 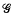→ 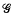{z0}. If this representation is not faithful, then 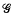contains a nontrivial element W such that W evaluated; at z0 is trivial. But W can evaluate to the identity only on a countable subset) of Δ, and there are only countably many choices for W in 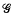Consequently there are at most countably many points zk in Δ such that 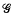{zk} is not isomorphic to Δ. Our main result can now be stated as follows.

MSC classification

Secondary: 20H99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 32 , Issue 2 , December 1985 , pp. 248 - 264
Copyright
Copyright © University College London 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beardon, A.. The Geometry of Discrete Groups (Springer, New York, Heidelberg, Berlin, 1983).CrossRefGoogle Scholar
2.Culler, M. and Shalen, P.. Varieties of group representations and splittings of 3-manifolds. Ann. of Math., 117 (1983), 109–146.CrossRefGoogle Scholar
3.Jørgensen, T.. On discrete groups of Möbius transformations. Amer. J. Math., 98 (1976), 739–749.CrossRefGoogle Scholar
4.Jørgensen, T.. A note on subgroups of SL (2, ℂ), Quart. J. Math. Oxford (2), 28 (1977), 209–212.CrossRefGoogle Scholar
5.Greenburg, L.. Homomorphisms of triangle groups into PSL (2, ℂ). Riemann Surfaces and Related Topics, Proceedings of the 1978 Stony Brook Conference (Princeton, 1979).Google Scholar
6.Lang, S.. Introduction to Algebraic Geometry (Interscience, New York, 1958).Google Scholar
7.Lyndon, R. and Ullman, J.. Groups generated by two parabolic linear fractional transformations. Canad. J. Math., 22 (1970), 1388–1403.Google Scholar
8.Marden, A.. The geometry of finitely generated Kleinian groups, Ann. of Math., 99 (1974), 383–462.CrossRefGoogle Scholar
9.Riley, R.. Applications of a computer implementation of Poincare's Theorem on Fundamental Polyhedra. Math. Comp., 40 (1983), 607–632.Google Scholar
10.Riley, R.. Discrete parabolic representations of link groups. Mathematika, 22 (1975), 141–150.CrossRefGoogle Scholar
11.Riley, R.. Nonabelian representations of 2-bridge knot groups. Quart. J. Math. Oxford (2), 35 (1984), 191–208.CrossRefGoogle Scholar
12.Selberg, A.. On discontinuous groups in higher dimensional symmetric spaces. Contributions to Function Theory (Bombay, 1960), 147–164.Google Scholar
13.Sullivan, D.. Quasi Conformal Homeomorphisms and Dynamics II: Structural Stability Implies Hyperbolicity for KJeinian Groups. To appear in Ada Math.Google Scholar
14.Thurston, W.. The Geometry and Topology of Three-Manifolds. Expected (Princeton, 1996).Google Scholar
15.Zariski, O.. Local uniformization on algebraic varieties. Collected Papers, Vol. I (M.I.T., 1972), 376–378 (especially Theorem U2 and discussion of and reference to other papers).Google Scholar