Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T11:00:22.633Z Has data issue: false hasContentIssue false
  • English
  • Français

Further lattice packings in high dimensions

Published online by Cambridge University Press:  26 February 2010

A. Bos ,
J. H. Conway  and
N. J. A. Sloane
A. Bos
Affiliation:
Corporate ISA, N. V. Philips' Gloeilampenfabrieken, 5600 MD, Eindhoven, Netherlands
J. H. Conway
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Cambridge, CB2 1SB
N. J. A. Sloane
Affiliation:
Mathematics and Statistics Research Center, Bell Laboratories, Murray Hill, NJ 07974, U.S.A.
Get access

Abstract

Barnes and Sloane recently described a “general construction” for lattice packings of equal spheres in Euclidean space. In the present paper we simplify and further generalize their construction, and make it suitable for iteration. As a result we obtain lattice packings in ℝm with density Δ satisfying 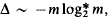, as m → ∞ where 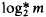is the smallest value of k for which the k-th iterated logarithm of m is less than 1. These appear to be the densest lattices that have been explicitly constructed in high-dimensional space. New records are also established in a number of lower dimensions, beginning in dimension 96.

Type
Research Article
Information
Mathematika , Volume 29 , Issue 2 , December 1982 , pp. 171 - 180
Copyright
Copyright © University College London 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barnes, E. S. and Sloane, N. J. A.. New lattice packings of spheres, Canad. J. Math., to appear.Google Scholar
2.Barnes, E. S. and Wall, G. E.. Some extreme forms defined in terms of Abelian groups. J. Australian Math. Soc, 1 (1959), 47–63.CrossRefGoogle Scholar
3.Bos, A.. Sphere packings in high–dimensional space. Preprint.Google Scholar
4.Bos, A.. Upper bounds for sphere packings in Euclidean space. IEEE IT Transactions on Information Theory. To appear.Google Scholar
5.Conway, J. H. and Sloane, N. J. A.. Laminated lattices. Annals of Math., to appear.Google Scholar
6.Delsarte, P.. Four fundamental parameters of a code and their combinatorial significance. Information and Control, 23 (1973), 407–438.CrossRefGoogle Scholar
7.Kabatiansky, G. A. and Levenshtein, V. I.. Bounds for packings on a sphere and in space (in Russian). Problemy Peredachi Informatsii, 14 (No. 1, 1978), 3–25. English translation in Problems of Information Transmission, 14 (1978), 1-17.Google Scholar
8.Leech, J.. Some sphere packings in higher space. Canad. J. Math., 16 (1964), 657–682.CrossRefGoogle Scholar
9.Leech, J.. Notes on sphere packings. Canad. J. Math., 19 (1967), 251–267.CrossRefGoogle Scholar
10.Leech, J. and Sloane, N. J. A.. New sphere packings in dimensions 9-15. Bull. Amer. Math. Soc, 76 (1970), 1006–1010.CrossRefGoogle Scholar
11.Leech, J. and Sloane, N. J. A.. New sphere packings in more than 32 dimensions. Proc. Second Chapel Hill Conference on Combinatorial Mathematics and its Applications (Univ. of North Carolina at Chapel Hill, 1970), 345–355.Google Scholar
12.Leech, J. and Sloane, N. J. A.. Sphere packings and error–correcting codes. Canad. J. Math., 23 (1971), 718–745.CrossRefGoogle Scholar
13.MacWilliams, F. J. and Sloane, N. J. A.. The Theory of Error–Correcting Codes (North–Holland, Amsterdam, 3rd printing, 1981).Google Scholar
14.Rogers, C. A.. Packing and Covering (Cambridge University Press, Cambridge, 1964).Google Scholar
15.Sloane, N. J. A.. Sphere packings constructed from BCH and Justesen codes. Mathematika, 19 (1972), 183–190.CrossRefGoogle Scholar
16.Sloane, N. J. A.. Codes over GF(4) and complex lattices. J. Algebra, 52 (1978), 168–181.CrossRefGoogle Scholar
17.Sloane, N. J. A.. Self-dual codes and lattices, in Relations Between Combinatorics and Other Parts of Mathematics, Proc. Sympos. Pure Math., 34 (Amer. Math. Soc, Providence, RI, 1979), 273–308CrossRefGoogle Scholar
18.Sloane, N. J. A.. Recent bounds for codes, sphere packings and related problems obtained by linear programming and other methods. In Papers in Algebra, Analysis and Statistics, edited by R. Lidl. Contemporary Mathematics, 9 (Amer. Math. Soc, 1982), 153–185CrossRefGoogle Scholar