Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-04T21:42:25.540Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FINITE SECTION METHOD FOR DISSIPATIVE OPERATORS

Part of: Special classes of linear operators Ordinary differential operators

Published online by Cambridge University Press:  14 May 2014

Marco Marletta  and
Sergey Naboko
Marco Marletta
Affiliation:
Wales Institute of Mathematical and Computational Sciences, School of Mathematics, Cardiff University, Senghennydd Road, Cardiff CF24 4AG,U.K. email [email protected]
Sergey Naboko
Affiliation:
School of Mathematics, Statistics and Actuarial Science, The University of Kent, Canterbury, Kent CT2 7NZ,U.K. email [email protected]
Get access

Abstract

We show that for self-adjoint Jacobi matrices and Schrödinger operators, perturbed by dissipative potentials in 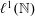$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\ell ^1({\mathbb{N}})$ and 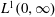$L^1(0,\infty )$ respectively, the finite section method does not omit any points of the spectrum. In the Schrödinger case two different approaches are presented. Many aspects of the proofs can be expected to carry over to higher dimensions, particularly for absolutely continuous spectrum.

MSC classification

Secondary: 47B36: Jacobi (tridiagonal) operators (matrices) and generalizations 34L05: General spectral theory 34L15: Eigenvalues, estimation of eigenvalues, upper and lower bounds 34L40: Particular operators (Dirac, one-dimensional Schrödinger, etc.)
Type
Research Article
Information
Mathematika , Volume 60 , Issue 2 , July 2014 , pp. 415 - 443
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aceto, L., Ghelardoni, P. and Marletta, M., Numerical computation of eigenvalues in spectral gaps of Sturm–Liouville operators. J. Comput. Appl. Math. 189 2006, 453–470.Google Scholar
Akhiezer, N. I. and Glazman, M., Theory of Linear Operators in Hilbert Space, Vol. II, Pitman (London, 1981).Google Scholar
Brown, B. M., McCormack, D., Evans, W. D. and Plum, M., On the spectrum of second order differential operators with complex coefficients. Proc. R. Soc. Lond. Ser. A 455 1999, 1235–1257.Google Scholar
Chernyavskaya, N. and Shuster, L., Estimates for Green’s Function of the Sturm–Liouville operator. J. Differential Equations 111 1994, 410–420.Google Scholar
Chandler-Wilde, S. and Davies, E. B., Spectrum of a Feiberg-Zee random hopping matrix. J. Spectr. Theory 2 2012, 147–179.Google Scholar
Chandler-Wilde, S. and Lindner, M., Limit Operators, Collective Compactness, and the Spectral Theory of Infinite Matrices (Memoirs of the American Mathematical Society 210), American Mathematical Society (Providence, RI, 2011).CrossRefGoogle Scholar
Clark, S. and Gesztesy, F., On Weyl–Titchmarsh theory for singular finite difference Hamiltonian systems. J. Comput. Appl. Math. 171 2004, 151–184.Google Scholar
Davies, E. B. and Plum, M., Spectral Pollution. IMA J. Numer. Anal. 24 2004, 417–438.Google Scholar
Gohberg, I. C. and Kreĭn, M. G., Introduction to the Theory of Linear Nonself-adjoint Operators (Translations of Mathematical Monographs 18) (Translated from the Russian by A. Feinstein), American Mathematical Society (Providence, RI, 1969).Google Scholar
Embree, M. and Trefethen, L. N., Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators, Princeton University Press (Princeton, NJ, 2005).Google Scholar
Hansen, A., On the solvability complexity index, the n-pseudospectrum and approximations of spectra of operators. J. Amer. Math. Soc. 24 2011, 81–124.Google Scholar
Levitan, B. M., Inverse Sturm–Liouville Problems (Translated from the Russian by O. Efimov), VSP (Zeist, 1987).Google Scholar
Levitin, M. and Shargorodsky, E., Spectral pollution and second order relative spectra for self-adjoint operators. IMA J. Numer. Anal. 24 2004, 393–416.Google Scholar
Lindner, M., Infinite Matrices and their Finite Sections: An Introduction to the Limit Operator Method, Birkhäuser (Basel, Boston, Berlin, 2006).Google Scholar
Lindner, M. and Roch, S., Finite sections of random Jacobi operators. SIAM J. Numer. Anal. 50 2012, 287–306.Google Scholar
Markushevich, A. I., Theory of functions of a complex variable, Vol. II (Revised English edition translated and edited by R. A. Silverman), Prentice-Hall, Inc (Englewood Cliffs, NJ, 1965).Google Scholar
Marletta, M., Neumann–Dirichlet maps and analysis of spectral pollution for non-self-adjoint elliptic PDEs with real essential spectrum. IMA J. Numer. Anal. 30 2010, 917–939.Google Scholar
Marletta, M. and Scheichl, R., Eigenvalues in spectral gaps of differential operators. J. Spectr. Theory 2 2012, 293–320.Google Scholar
Monaquel , S. J. and Schmidt, K. M., On M-functions and operator theory for non-self-adjoint discrete Hamiltonian systems. J. Comput. Appl. Math. 208 2007, 82–101.Google Scholar
Sims, A. R., Secondary conditions for linear differential operators of the second order. J. Math. Mech. 6 1957, 247–285.Google Scholar
Stolz , G. and Weidmann, J., Approximation of isolated eigenvalues of general singular ordinary differential operators. Results Math. 28 1995, 345–358.CrossRefGoogle Scholar
Zimmermann, S. and Mertins, U., Variational bounds to eigenvalues of self-adjoint eigenvalue problems with arbitrary spectrum. Z. Anal. Anwend. 14 1995, 327–345.Google Scholar