Article contents
Double packing of spheres: a new upper bound
Published online by Cambridge University Press: 26 February 2010
Extract
Let S be a set of points in n-dimensional space, and suppose that an open sphere of unit radius is centred at each point of S. Suppose that no point of space is an inner point of more than two spheres. We say that S provides a double packing for spheres of unit radius. We define δ2(S), the density of this double packing, to be
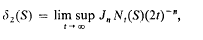
where Jn is the volume of a sphere of unit radius, and Nt(S) is the number of points of S inside a cube of side 2t, centred at the origin O. We define δ2, the density of closest double packing, to be
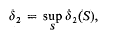
where the supremum is taken over all sets S with the property described above.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1968
References
- 6
- Cited by


