Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-04T06:45:31.986Z Has data issue: false hasContentIssue false
  • English
  • Français

Diophantine approximation of linear forms over an algebraic number field

Published online by Cambridge University Press:  26 February 2010

T. W. Cusick
T. W. Cusick
Affiliation:
State University of New York at Buffalo.
Get access

Extract

This paper gives an algorithm for generating all the solutions in integers x0, x1…, xn of the inequality

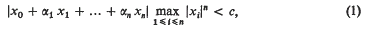
where 1, α1, …,αn are numbers, linearly independent over the rationals, in a real algebraic number field of degree n + 1 ≥ 3 and c is any sufficiently large positive constant. It is well known [2, p. 79] that if c is small enough, then (1) has no integer solutions with x1…, xn not all zero.

Type
Research Article
Information
Mathematika , Volume 20 , Issue 1 , June 1973 , pp. 16 - 23
Copyright
Copyright © University College London 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Borevich, Z. I. and Shafarevich, I. R., Number Theory (New York: Academic Press, 1966).Google Scholar
2. Cassels, J. W. S., An Introduction to Diophantine Approximation (Cambridge University Press, 1957).Google Scholar
3. Cusick, T. W., “Diophantine approximation of ternary linearforms”, Math. Comput., 25 (1971), 163–180.Google Scholar
4. Cusick, T. W., “Diophantine approximation of ternary linear forms II”, Math. Comput. 26 (1972), 977–993.Google Scholar
5. Cusick, T. W., “Formulas for some Diophantine approximation constants”, Math. Ann., 197 (1972), 182–188.CrossRefGoogle Scholar
6. Cusick, T. W., “Formulas for some Diophantine approximation constants II”, (to appear).Google Scholar
7. Davenport, H. and Schmidt, W. M., “Dirichlet's theorem on Diophantine approximation”, Symposia Mathematica IV— Proceedings of a Conference on the theory of numbers, Rome, 1968 (New York: Academic Press, 1970), 113–132.Google Scholar
8. Lesca, J., Sur les approximations diophantiennes à une dimension, thesis (University of Grenoble, France, 1968).Google Scholar