Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T16:23:59.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Diophantine approximation and a lower bound for Hausdorff dimension

Published online by Cambridge University Press:  26 February 2010

M. M. Dodson ,
B. P. Rynne  and
J. A. G. Vickers
M. M. Dodson
Affiliation:
Department of Mathematics, University of York, York, YO1 5DD
B. P. Rynne
Affiliation:
Department of Mathematics, University of Dundee, Dundee, DD1 4HN
J. A. G. Vickers
Affiliation:
Department of Mathematics, University of Southampton, Southampton, SO9 5NH
Get access

Extract

Sets of the general form

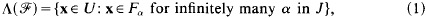
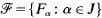where U is a subset of ℛk and is a family of subsets of U indexed by a set J, are common in the theory of Diophantine approximation [4, 7, 18, 19]. They are also closely connected with exceptional sets arising in analysis and with sets of “small divisors” in dynamical systems [1, 8, 15”. When J is the set of positive integers ℕ, the set Λ(ℱ) is of course the lim-sup of the sequence of sets Fj, j = 1, 2,… [11, p. 1]. We will also call sets of the form (1), with the more general index set J, lim-sup sets. When such lim-sup sets have Lebesgue measure zero, it is of interest to determine their Hausdorff dimension. It is usually difficult to obtain a good lower bound for the Hausdorff dimension (and it can be much harder to determine than an upper bound). In this paper we will obtain a lower bound for the dimension of lim-sup sets of the form (1) for a fairly general class of families ℕ which includes a range of results in the theory of Diophantine approximation. This lower bound depends explicitly on the geometric structure and distribution in U of the sets Fα in ℕ.

Type
Research Article
Information
Mathematika , Volume 37 , Issue 1 , June 1990 , pp. 59 - 73
Copyright
Copyright © University College London 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Arnol'd, V. I.. Geometrical Methods in the Theory of Ordinary Differential Equations, translated by Szücs, J. (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
2.Baker, A. and Schmidt, W.. Diophantine approximation and Hausdorfi dimension. Proc. London Math. Soc, 21 (1970), 1–11.Google Scholar
3.Bernik, V. I.. Applications of measure theory and Hausdorff dimension to the theory of Diophantine approximation, in New Advances in Transcendence Theory, ed. Baker, A. (Cambridge University Press, 1988), 25–36.CrossRefGoogle Scholar
4.Bernik, V. I. and Melnichuk, Y. V.. Diophantine Approximation and Hausdorff Dimension (Akad. Nauk Byeloruss. SSR, 1988).Google Scholar
5.Besicovitch, A. S.. Sets of fractional dimension (IV): On rational approximation to real numbers. J. London Math. Soc, 9 (1934), 126–131.Google Scholar
6.Bovey, J. D. and Dodson, M. M.. The Hausdorff dimension of systems of linear forms. Ada Arith., 45 (1986), 337–358.Google Scholar
7.Cassels, J. W. S.. An Introduction to Diophantine Approximation (Cambridge University Press, Cambridge, 1957).Google Scholar
8.Dodson, M. M. and Vickers, J. A. G.. Exceptional sets in Kolmogorov-Arnol'd-Moser theory. J. of Physics A, 19 (1986), 349–374.Google Scholar
9.Dodson, M. M., Rynne, B. P. and Vickers, J. A. G.. Metric Diophantine approximation and Hausdorff dimension on manifolds. Math. Proc. Cam. Phil. Soc, 105 (1989), 547–558.CrossRefGoogle Scholar
10.Eggleston, H. G.. Sets of fractional dimension which occur in some problems in number theory. Proc. London Math. Soc, 54 (1952), 42–93.CrossRefGoogle Scholar
11.Falconer, K. J.. The Geometry of Fractal Sets (Cambridge University Press, Cambridge, 1985).CrossRefGoogle Scholar
12.Falconer, K. J.. Classes of sets with large intersection. Mathematika, 32 (1985), 191–205.CrossRefGoogle Scholar
13.Falconer, K. J.. Fractal Geometry–Mathematical Foundations and Applications (J. Wiley, Chichester, 1990).Google Scholar
14.Gruber, P.. Uber das Produkt inhomogener Linearformen. Acta Arith., 13 (1967), 9–27.Google Scholar
15.Herman, M.. Recent results and some open questions on Siegel's linearisation theorem of germs of complex analytic diffeomorphisms of ℂn near a fixed point, In Proceedings of the 8th International Congress on Mathematical Physics, Marseilles 1986, eds. Mebkhout, M. and Sénéor, R. (World Scientific, Singapore, 1987).Google Scholar
16.Jarník, V.. Diophantische Approximationen und Hausdorffsches Mass. Mat. Sb., 36 (1929), 371–382.Google Scholar
17.Jarník, V.. Uber die simultanen diophantischen Approximation. Math. Zeitschrift, 33 (1931), 503–543.Google Scholar
18.Sprindžuk, V. G.. Metric Theory of Diophantine Approximations, translated by Silverman, R. A. (Wiley, New York, 1979).Google Scholar
19.Schmidt, W. M.. Diophantine Approximation. Lecture Notes in Mathematics 785 (Springer-Verlag, Berlin, 1980).Google Scholar