Article contents
Covering space by spheres
Published online by Cambridge University Press: 26 February 2010
Extract
Let Λ be a lattice in three-dimensional space with the property that the spheres of radius 1 centred at the points of Λ cover the whole of space. In other words, every point of space is at a distance not more than 1 from some point of Λ. It was proved by Bambah that then
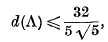
equality occurring if and only if Λ is a body-centred cubic lattice with the side of the cube equal to 4/√5. Another way of stating the result is to say that the least density of covering of three-dimensional space by equal spheres, subject to the condition that the centres of the spheres form a lattice, is 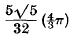 . Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.
. Another proof of Bambah's result was given recently by Barnes. Both proofs depend on the theory of reduction of ternary quadratic forms.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1956
References
* Bambah, R. P., Proc. Nat. Inst. Sci. India, 20 (1954), 25–52.Google Scholar
† Barnes, E. S., Canadian J. of Math., 8 (1956), 293–304.CrossRefGoogle Scholar
‡ An appeal to this could easily be avoided.
- 16
- Cited by


