Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T05:13:05.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Convex bodies of constant outer p-measure

Published online by Cambridge University Press:  26 February 2010

William J. Firey
William J. Firey
Affiliation:
Oregon State University, Corvallis, Oregon, U.S.A.
Get access

Extract

Suppose K is a convex body in Euclidean n-space En and that all the orthogonal projections of K onto p-dimensional linear subspaces have the same p-dimensional volume, that is K has constant outer p-measure. If p = 1, this means that K is of constant width; if p = n − 1, this means that K has constant brightness. It is known that, when the boundary of K is smooth enough to admit principal radii of curvature R1, …, Rn-1 as functions of the outer normal u, and if we define Fp(u) to be the p-th elementary symmetric function of these radii, then, when K has constant width,

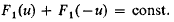
Type
Research Article
Information
Mathematika , Volume 17 , Issue 1 , June 1970 , pp. 21 - 27
Copyright
Copyright © University College London 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Blaschke, W., Kreis und Kugel, (Leipzig, 1916).CrossRefGoogle Scholar
2.Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper, (Berlin, 1934).Google Scholar
3.Byrd, P. F. and Friedman, M. D., Handbook of Elliptic Integrals for Engineers and Physicists, (Berlin-Göttingen-Heidelberg, 1954).CrossRefGoogle Scholar
4.Chakerian, G. D., “Sets of constant relative width”, Trans. Amer. Math. Soc., 129 (1967), 26–37.CrossRefGoogle Scholar
5.Firey, W. J., “The determination of convex bodies from their mean radius of curvature functions”, Mathematika, 14 (1967), 1–14.CrossRefGoogle Scholar
6.Klee, V. L., “Is a body spherical if its HA-measurements are constant?”, Amer. Math. Monthly, 76 (1969), 539–542.CrossRefGoogle Scholar
7.Perron, O., Algebra I, 3rd edition (Berlin, 1951).Google Scholar