Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T17:37:55.913Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely 0-simple semigroups of left quotients

Part of: Semigroups

Published online by Cambridge University Press:  26 February 2010

Mario Petrich
Mario Petrich
Affiliation:
21420 Bol, Brač, Croatia.
Get access

Abstract

A subsemigroup S of a semigroup Q is a left order in Q, and Q is a semigroup of left quotients of S, if every element of Q can be written as a−1b for some a, b∈S with a belonging to a group 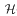-class of Q. Necessary and sufficient conditions on a semigroup S are obtained in order that S be a left order in a completely 0-simple semigroup Q. The class of all completely 0-simple semigroups of left quotients of S is related to the set of certain left congruences on S. Axioms are provided for semigroups which occur in the discussion of left orders in completely 0-simple semigroups.

MSC classification

Secondary: 20M10: General structure theory
Type
Research Article
Information
Mathematika , Volume 51 , Issue 1-2 , December 2004 , pp. 111 - 122
Copyright
Copyright © University College London 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ánh, P. N., Gould, V. and Márki, L.. Completely 0-simple semigroups of left quotients of a semigroup. Int. J. Algebra Comp., 6 (1996), 143–153.CrossRefGoogle Scholar
2.Clifford, A. H. and Preston, G. B.. The algebraie theory of semigroups. Vol. I (Math. Surveys No. 7, Amer. Math. Soc., Providence, 1961).Google Scholar
3.Fountain, J. and Petrich, M.. Brandt semigroups of left quotients. Math. Proc. Cambridge Philos. Soc, 98 (1985), 413–426.CrossRefGoogle Scholar
4.Fountain, J. and Petrich, M.. Completely 0-simple semigroups of quotients. J. Algebra. 101 (1986), 365–402.CrossRefGoogle Scholar
5.Fountain, J. and Petrich, M.. Completely 0-simple semigroups of quotients III. Math. Proc. Cambridge Philos. Soc, 105 (1989), 263–275.CrossRefGoogle Scholar
6.Fountain, J. and Petrich, M.. Orders in normal bands of groups. Mathematika. 43 (1996). 295–319.CrossRefGoogle Scholar
7.Gould, V.. Orders in semigroups. Contributions to Algebra., Proc. Salzburg Conf. 1986. Verlag Holder-Pichler-Tempsky, (Vienna 1987), 163–169.Google Scholar
8.Gould, V.. Absolutely flat completely 0-simple semigroups of left quotients. J. Pure Appl. Algebra, 55 (1988), 261–288.CrossRefGoogle Scholar
9.Gould, V.. Left orders in regular H-semigroups II. Glasgow Math. J., 32 (1990), 95–108.CrossRefGoogle Scholar
10.Gould, V.. Left orders in regular W-semigroups I. J. Algebra, 141 (1991), 11–35.CrossRefGoogle Scholar
11.McAlister, D. B.. One-to-one partial right translations of a right cancellative semigroup. J. Algebra, 43 (1976), 231–251.CrossRefGoogle Scholar