Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T17:20:55.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorics and linear algebra of Freiman's isomorphism

Part of: Sequences and sets

Published online by Cambridge University Press:  26 February 2010

Sergei V. Konyagin  and
Vsevolod F. Lev
Sergei V. Konyagin
Affiliation:
Department of Mechanics and Mathematics, Moscow State University, Moscow, 119899, Russia. E-mail: [email protected]
Vsevolod F. Lev
Affiliation:
Department of Mathematics, The University of Georgia, Athens, GA 30602, U.S.A.
Get access

Abstract

An original linear algebraic approach to the basic notion of Freiman's isomorphism is developed and used in conjunction with a combinatorial argument to answer two questions, posed by Freiman about 35 years ago.

First, the order of growth is established of t(n), the number of classes isomorphic n-element sets of integers: t(n) = n(2 + σ(1))n. Second, it is proved linear Roth sets (sets of integers free of arithmetic progressions and having Freiman rank 1) exist and, moreover, the number 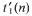of classes of such cardinality n is amazingly large; in fact, it is “the same as above”: .

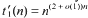MSC classification

Secondary: 11B13: Additive bases, including sumsets
Type
Research Article
Information
Mathematika , Volume 47 , Issue 1-2 , December 2000 , pp. 39 - 51
Copyright
Copyright © University College London 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Freiman, G.. Foundations of a structure theory of set addition, Kazan 1966 [Russian]. English translation in: Translations of Math. Monographs 37 (1973), American Math. Soc., Providence, RI.Google Scholar
2.Asaphova, G. A.. On one type of Latin squares of order 6, in: Number-theoretic investigations in Markov spectrum and structure theory of set addition, Kalinin State University, Moscow, 1973 [Russian].Google Scholar