Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-09T13:30:44.562Z Has data issue: false hasContentIssue false
  • English
  • Français

A classifying space for the contact pseudogroup

Published online by Cambridge University Press:  26 February 2010

C. B. Thomas
C. B. Thomas
Affiliation:
Department of Mathematics, University College London
Get access

Extract

§1. With respect to coordinates {z, x1, …, xq+1, …, x2q} a contact transformation is a local diffeomorphism of ℝ2q+1, which preserves the 1-form

up to multiplication by a non-zero real valued function. The family of such maps contains identities, inverses and admits a partial composition law; denote it by 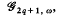the contact pseudogroup. Passing to germs of local diffeomorphisms we obtain a topological groupoid Γ2q+1, ω, to which by any of several constructions, see [1] for example, there corresponds a classifying space BΓ2q+1, ω, By analogy with BΓq this space classifies codimension (2q + l)-foliations, which locally admit a contact structure normal to the leaves. In particular, at least when q is odd, the structural group of the normal bundle reduces to Uq. We shall be most interested in the case, when the foliation is by points, and the underlying manifold M2q+1 admits a global 1-form co such that

Type
Research Article
Information
Mathematika , Volume 25 , Issue 2 , December 1978 , pp. 191 - 201
Copyright
Copyright © University College London 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bott, R., Shulman, H., Stasheff, J.. “On the de Rham theory of certain classifying spaces.” Advances in Math., 20 (1976), 43–56.CrossRefGoogle Scholar
2.Gray, J. W.. “Some global properties of contact structures.” Annals of Math., 69 (1959), 421–450.CrossRefGoogle Scholar
3.Haefliger, A.. “Lectures on the theorem of Gromov.” Proc. Liverpool singularities Symposium II, Lecture Notes in Math. 209 (Springer Verlag, 1971), pp. 128–141.CrossRefGoogle Scholar
4.Haefliger, A., “Sur les classes characteristiques des feuilletages,” Sem. Bourbaki All, Lecture Notes in Math. 317 (Springer Verlag, 1973), pp. 239–260.Google Scholar
5.Hirzebruch, F. and Mayer, K. H.. O(n)—Mannigfaltigkeiten, exotische Sphdren und Singularitaten, Lecture Notes in Math. 5 (Springer Verlag, 1968).CrossRefGoogle Scholar
6.Lutz, R. and Meckert., C. “Structures de contact sur certaines spheres exotiques.” Compt. Rend., Acad. Sci. (Serie A) 282 (1976).Google Scholar
7.Martinet, J.. “Formes de contact sur les varietes de dimension 3.” Proc. Liverpool singularities symposium II, Lecture Notes in Math. 209 (Springer Verlag, 1971), 142–63.CrossRefGoogle Scholar
8.Orlik, P. and Wagreich, P.. “Seifert n-manifolds.” Inventiones Math., 28 (1975), 137–159.CrossRefGoogle Scholar
9.Perchik, J.. “Cohomology of Hamiltonian and related formal vector field Lie algebras.” Topology, 15 (1976), 395–404.CrossRefGoogle Scholar
10.Steenrod, N.. Topology of fibre bundles (Princeton University Press, 1951).CrossRefGoogle Scholar
11.Stong, R.. “Contact manifolds.” J. Differential Geometry, 9 (1974), 219–238.CrossRefGoogle Scholar
12.Thomas, C. B.. “Almost regular contact manifolds.” J. Differential geometry, 11 (1976), 521–533.CrossRefGoogle Scholar