Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T16:09:29.563Z Has data issue: false hasContentIssue false
  • English
  • Français

A class number relation in Frobenius extensions of number fields

Published online by Cambridge University Press:  26 February 2010

Colin D. Walter
Colin D. Walter
Affiliation:
Department of Mathematics, University College, Belfield, Dublin 4, Ireland.
Get access

Extract

Let K/k be a normal extension of algebraic number fields whose Galois group G is a Frobenius group. Then K/k is said to be a Frobenius extension. Most of the structure of the unit group and of the ideal class group of K is determined by that; of the subfields fixed by the Frobenius kernel N and by a complement F. Here this is investigated when G is a maximal or metacyclic Frobenius group. In particular, the results apply firstly to the normal closure of 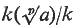where a ∊ k and p is a rational prime, and, secondly, when G is a dihedral group of order 2n for an odd integer n. A. Scholz, taking n = p = 3, was the first to consider this problem.

Type
Research Article
Information
Mathematika , Volume 24 , Issue 2 , December 1977 , pp. 216 - 225
Copyright
Copyright © University College London 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Brauer, R.. “Beziehungen zwischen Klassenzahlen von Teilkôrpern eines galoisschen Kôrpers”, Math. Nachr., 4 (1951), 158–174.CrossRefGoogle Scholar
2.Halter-Koch, F.. “Einheiten und Divisorenklassen in Galois'schen algebraischen Zahlkôrpern mit Diedergruppe der Ordnung 21 für eine ungerade Primzahl”, Acta Arithmetica, 33 (1977), 353–364.CrossRefGoogle Scholar
3.Halter-Koch, F.. “Die Struktur der Einheitengruppe für eine Klasse metazyklischer Erweiterungen algebraischer Zahlkürper”, to appear in J. f. reine u. angew. Math.Google Scholar
4.Halter-Koch, F. and Moser, N. “Sur le nombre de classes de certaines extensions metacycliques sur Q ou sur un corps quadratique imaginaire”, j. Math. Soc. Japan.Google Scholar
5.Honda, T.. “On the absolute ideal class groups of relatively meta-cyclic number fields of a certain type”, Nagoya Math. J. 17 (1960), 171–179.CrossRefGoogle Scholar
6.Jehne, W.. “Über die Einheiten- und Divisorenklassengruppe von reellen Frobsniuskörpern von Maximaltyp”, Math. Zeit., 152 (1977), 223–252.CrossRefGoogle Scholar
7.Kuroda, S..“Über die Klassenzahlen algebraischer Zahlkörper”, Nagoya Math. J., 1 (1950), 1–10CrossRefGoogle Scholar
8.Moser, N.. “Unités et nombre de classes d'une extension galoisienne diédrale de Q”, Univ. Sci. Med. Grenoble, 1973-4.Google Scholar
9.Walter, C.. Class number relations in algebraic number fields (Thesis, Cambridge Univ., April, 1976)Google Scholar
10.Walter, C.. “Brauer's class number relation“, Acta Arith., to appear.Google Scholar
11.Walter, C.. “Kuroda's class number relation”, Acta Arith., to appear.Google Scholar