Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hall, R.R.
2002.
A Wirtinger Type Inequality and the Spacing of the Zeros of the Riemann Zeta-Function.
Journal of Number Theory,
Vol. 93,
Issue. 2,
p.
235.
Hall, R.R.
2002.
Generalized Wirtinger inequalities, random matrix theory, and the zeros of the Riemann zeta-function.
Journal of Number Theory,
Vol. 97,
Issue. 2,
p.
397.
Ng, Nathan
2004.
The fourth moment of ζ′(ρ).
Duke Mathematical Journal,
Vol. 125,
Issue. 2,
Hall, R.R.
2004.
Large spaces between the zeros of the Riemann zeta-function and random matrix theory.
Journal of Number Theory,
Vol. 109,
Issue. 2,
p.
240.
Garunks˘tis, Ramūnas
and
Steuding, Jörn
2005.
Simple zeros and discrete moments of the derivative of the Riemann zeta-function.
Journal of Number Theory,
Vol. 115,
Issue. 2,
p.
310.
Hall, R. R.
2005.
A New Unconditional Result about Large Spaces Between Zeta Zeros.
Mathematika,
Vol. 52,
Issue. 1-2,
p.
101.
Королeв, Максим Александрович
and
Korolev, Maxim Aleksandrovich
2008.
О больших расстояниях между соседними нулями дзета-функции Римана.
Известия Российской академии наук. Серия математическая,
Vol. 72,
Issue. 2,
p.
91.
Korolev, M A
2008.
On large distances between consecutive zeros of the Riemann zeta-function.
Izvestiya: Mathematics,
Vol. 72,
Issue. 2,
p.
291.
Saker, SamirH
2010.
Applications of Wirtinger Inequalities on the Distribution of Zeros of the Riemann Zeta-Function.
Journal of Inequalities and Applications,
Vol. 2010,
Issue. 1,
p.
215416.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
307.
Hall, Richard R.
2012.
Some Four Dimensional Definite Integrals Arising from Zeta-Function Theory.
Computational Methods and Function Theory,
Vol. 12,
Issue. 2,
p.
565.
Turnage-Butterbaugh, Caroline L.
2014.
Gaps between zeros of Dedekind zeta-functions of quadratic number fields.
Journal of Mathematical Analysis and Applications,
Vol. 418,
Issue. 1,
p.
100.
Barrett, Owen
McDonald, Brian
Miller, Steven J.
Ryan, Patrick
Turnage-Butterbaugh, Caroline L.
and
Winsor, Karl
2015.
Gaps between zeros of GL(2) L-functions.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 1,
p.
204.
Bui, H. M.
Heap, Winston P.
and
Turnage-Butterbaugh, Caroline L.
2016.
GAPS BETWEEN ZEROS OF DEDEKIND ZETA-FUNCTIONS OF QUADRATIC NUMBER FIELDS. II.
The Quarterly Journal of Mathematics,
Vol. 67,
Issue. 3,
p.
467.
Banerjee, Debika
and
Minamide, Makoto
2016.
The average behaviour of the error term in a new kind of the divisor problem.
Journal of Mathematical Analysis and Applications,
Vol. 438,
Issue. 2,
p.
533.
Conrey, J. Brian
and
Turnage‐Butterbaugh, Caroline L.
2018.
On r‐gaps between zeros of the Riemann zeta‐function.
Bulletin of the London Mathematical Society,
Vol. 50,
Issue. 2,
p.
349.
Bui, H M
and
Milinovich, M B
2018.
Gaps between zeros of the Riemann zeta-function.
The Quarterly Journal of Mathematics,
Vol. 69,
Issue. 2,
p.
403.
Furuya, Jun
Minamide, T. Makoto
and
Tanigawa, Yoshio
2019.
Titchmarsh’s Method for the Approximate Functional Equations for , , and .
Canadian Journal of Mathematics,
Vol. 71,
Issue. 6,
p.
1465.
Korolev, Maxim A.
and
Shubin, Andrei V.
2020.
Trigonometric Sums and Their Applications.
p.
169.
Minamide, T. Makoto
and
Tanigawa, Yoshio
2020.
Mean square of the derivatives of Hardy's Z-function.
Journal of Mathematical Analysis and Applications,
Vol. 485,
Issue. 1,
p.
123772.


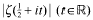 between successive zeros. Our results are to be independent of any unproved hypothesis. Put
between successive zeros. Our results are to be independent of any unproved hypothesis. Put