Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T12:34:55.183Z Has data issue: false hasContentIssue false
  • English
  • Français

The asymptotic formula in Waring's problem

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  26 February 2010

Kent D. Boklan
Kent D. Boklan
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, U.S.A.
Get access

Extract

Let s, k and n be positive integers and define rs,k(n) to be the number of solutions of the diophantine equation

in positive integers xi. In 1922, using their circle method, Hardy and Littlewood [2] established the asymptotic formula

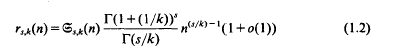
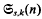whenever s≥(k−2)2k−1 + 5. Here , the singular series, relates the local solubility of (1.1). For each k we define 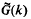to be the smallest value of s0 such that for all s ≥ s0 we have (1.2), the asymptotic formula in Waring's problem. The main result of this memoir is the following theorem which improves upon bounds of previous authors when k≤9.

MSC classification

Secondary: 11P05: Waring's problem and variants
Type
Research Article
Information
Mathematika , Volume 41 , Issue 2 , December 1994 , pp. 329 - 347
Copyright
Copyright © University College London 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Hall, R. and Tenenbaum, G.. The average orders of Hooley's Δ, functions, II. Compositio Math., 60 (1986), 163–186.Google Scholar
2.Hardy, G. H. and Littlewood, J. E.. Some problems of “Partitio Numerorum”; IV, The singular series in Waring's problem. Math. Z., 12 (1992), 161–188.CrossRefGoogle Scholar
3.Heath-Brown, D. R.. Weyl's Inequality, Hua's Inequality, and Waring's problem. J. London Math. Soc. (2), 38 (1988), 216–230.CrossRefGoogle Scholar
4.Hua, L.-K.. On Waring's problem. Quart. J. Math. Oxford, 9 (1938), 199–202.CrossRefGoogle Scholar
5.Vaughan, R. C.. The Hardy-Littlewood Method (Cambridge Univ. Press, London, 1981).Google Scholar
6.Vaughan, R. C.. On Waring's problem for cubes. J. reine angew. Math., 365 (1986), 122–170.Google Scholar
7.Vaughan, R. C.. On Waring's problem for smaller exponents, II. Mathematika, 33 (1986), 6–22,.CrossRefGoogle Scholar
8.Weyl, H.. Über ein Problem aus dem Gebeite der diophantischen Approximationen. Nachr. Akad. Wiss. Göttingen, (1914), 234–244.Google Scholar
9.Wooley, T. D.. On Vinogradov's Mean Value Theorem. Mathematika, 39 (1992), 379–399.CrossRefGoogle Scholar