Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rogers, C. A.
and
Taylor, S. J.
1963.
Additive set functions in Euclidean space. II.
Acta Mathematica,
Vol. 109,
Issue. 0,
p.
207.
Bressler, D. W.
and
Sion, M.
1964.
The Current Theory of Analytic Sets.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
207.
Larman, D. G.
1967.
On the selection of non‐σ‐finite subsets.
Mathematika,
Vol. 14,
Issue. 2,
p.
161.
Kaufman, Robert
1968.
On Hausdorff dimension of projections.
Mathematika,
Vol. 15,
Issue. 2,
p.
153.
Davies, Roy O.
1968.
A theorem on the existence of non‐σ‐finite subsets.
Mathematika,
Vol. 15,
Issue. 1,
p.
60.
Goodey, P. R.
1973.
Hausdorff measure functions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 74,
Issue. 1,
p.
87.
Larman, D. G.
1974.
On the Selection of Compact Subsets of Positive Measure from Analytic Sets of Positive Measure.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 3,
p.
665.
Gardner, R. J.
1982.
Measure Theory Oberwolfach 1981.
Vol. 945,
Issue. ,
p.
42.
Falconer, K. J.
1985.
Classes of sets with large intersection.
Mathematika,
Vol. 32,
Issue. 2,
p.
191.
Berman, Robert D.
and
Cohn, William S.
1986.
A radial phragmén–lindelöf theorem for functions of slow growth.
Complex Variables, Theory and Application: An International Journal,
Vol. 6,
Issue. 2-4,
p.
299.
Haase, H.
1986.
Non‐σ‐finite sets for packing measure.
Mathematika,
Vol. 33,
Issue. 1,
p.
129.
Barlow, Martin T.
and
Taylor, S. James
1992.
Local dimension and regular points.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 112,
Issue. 2,
p.
361.
Král, Josef
1994.
ICPT ’91.
p.
119.
Kr�l, Josef
1994.
Removability of singularities in potential theory.
Potential Analysis,
Vol. 3,
Issue. 1,
p.
119.
Falconer, K. J.
and
Mauldin, R. Daniel
2000.
Fubini‐type theorems for general measure constructions.
Mathematika,
Vol. 47,
Issue. 1-2,
p.
251.
Farah, Ilijas
and
Zapletal, Jindřich
2006.
Four and more.
Annals of Pure and Applied Logic,
Vol. 140,
Issue. 1-3,
p.
3.
Astala, K.
Clop, A.
Mateu, J.
Orobitg, J.
and
Uriarte-Tuero, I.
2008.
Distortion of Hausdorff measures and improved Painlevé removability for quasiregular mappings.
Duke Mathematical Journal,
Vol. 141,
Issue. 3,
Balka, Richárd
Darji, Udayan B.
and
Elekes, Márton
2016.
Hausdorff and packing dimension of fibers and graphs of prevalent continuous maps.
Advances in Mathematics,
Vol. 293,
Issue. ,
p.
221.
Zindulka, Ondřej
2018.
Mapping Borel Sets onto Balls and Self-similar Sets by Lipschitz and Nearly Lipschitz Maps.
International Mathematics Research Notices,
Harjulehto, Petteri
and
Hurri-Syrjänen, Ritva
2023.
On Choquet integrals and Poincaré-Sobolev inequalities.
Journal of Functional Analysis,
Vol. 284,
Issue. 9,
p.
109862.


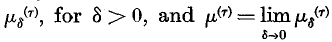 (see §3). When, for every
(see §3). When, for every 