Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T12:33:14.282Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic continuation of power series whose coefficients belong to an algebraic number field

Published online by Cambridge University Press:  26 February 2010

Stephen Gerig
Stephen Gerig
Affiliation:
The University of Western Australia, Perth, Australia.
Get access

Extract

An old theorem of Pólya and Carlson [2] states that, if the power series 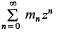has rational integer coefficients, positive radius of convergence, and can be continued analytically to a region that contains points outside the closed unit disc, then the function that the power series represents is rational. This result has been extended in a number of ways (cf. e.g. Petersson [4]). The present note gives a new extension based on a recent theorem of Güting [3]. My thanks to Professors Henry Helson and Raphael Robinson for introducing me to this subject.

Type
Research Article
Information
Mathematika , Volume 16 , Issue 2 , December 1969 , pp. 167 - 169
Copyright
Copyright © University College London 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bieberbach, Ludwig, Analytische Fortzetzung (Springer-Verlag, 1955).CrossRefGoogle Scholar
2.Carlson, F., “Über Potenzreihen mit ganzzahligen Koeffizienten”, Math. Zeit., 9 (1921), 1–13.CrossRefGoogle Scholar
3.Güting, R., “Approximation of algebraic numbers by algebraic numbers”, Mich. Math. Journal, 8 (1961), 149–159.CrossRefGoogle Scholar
4.Petersson, H., “Über Potenzreihen mit ganzen algebraischen Zahlenkoeffizienten”, Abh. Math. Sent. Hamburg, 8 (1931), 315–322.CrossRefGoogle Scholar