Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-23T07:11:56.027Z Has data issue: false hasContentIssue false
  • English
  • Français

AN INCLUSION–EXCLUSION IDENTITY FOR NORMAL CONES OF POLYHEDRAL SETS

Part of: General convexity Polytopes and polyhedra

Published online by Cambridge University Press:  05 February 2018

Daniel Hug  and
Zakhar Kabluchko
Daniel Hug
Affiliation:
Karlsruhe Institute of Technology (KIT), Department of Mathematics, Englerstr. 2, D-76128 Karlsruhe, Germany email [email protected]
Zakhar Kabluchko
Affiliation:
Institut für Mathematische Statistik, Westfälische Wilhelms-Universität Münster, Orléans–Ring 10, 48149 Münster, Germany email [email protected]
Get access

Abstract

For a non-empty polyhedral set 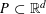$P\subset \mathbb{R}^{d}$, let 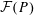${\mathcal{F}}(P)$ denote the set of faces of 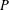$P$, and let 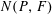$N(P,F)$ be the normal cone of 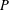$P$ at the non-empty face 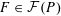$F\in {\mathcal{F}}(P)$. We prove the identity

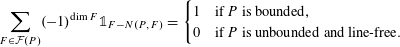$$\begin{eqnarray}\mathop{\sum }_{F\in {\mathcal{F}}(P)}(-1)^{\operatorname{dim}F}\unicode[STIX]{x1D7D9}_{F-N(P,F)}=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }P\text{ is bounded},\\ 0\quad & \text{if }P\text{ is unbounded and line-free}.\end{array}\right.\end{eqnarray}$$
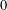Previously, this formula was known to hold everywhere outside some exceptional set of Lebesgue measure $0$ or for polyhedral cones. The case of a not necessarily line-free polyhedral set is also covered by our general theorem.

MSC classification

Primary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52B11: $n$-dimensional polytopes
Secondary: 52A55: Spherical and hyperbolic convexity
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 124 - 136
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amelunxen, D. and Lotz, M., Intrinsic volumes of polyhedral cones: a combinatorial perspective. Discrete Comput. Geom. 58(2) 2017, 371–409.Google Scholar
Cowan, R., Identities linking volumes of convex hulls. Adv. Appl. Probab. 39(3) 2007, 630–644.Google Scholar
Cowan, R., Recurrence relationships for the mean number of faces and vertices for random convex hulls. Discrete Comput. Geom. 43(2) 2010, 209–220.Google Scholar
Glasauer, S., Integralgeometrie konvexer Körper im sphärischen Raum. PhD Thesis, University of Freiburg, 1995. Available at: http://www.hs-augsburgde/∼glasauer/publ/diss.pdf.Google Scholar
Glasauer, S., An Euler-type version of the local Steiner formula for convex bodies. Bull. Lond. Math. Soc. 30(6) 1998, 618–622.Google Scholar
Hug, D., Measures, curvatures and currents in convex geometry. Habilitation Thesis, University of Freiburg, Germany, 1999.Google Scholar
Kabluchko, Z., Last, G. and Zaporozhets, D., Inclusion–exclusion principles for convex hulls and the Euler relation. Discrete Comput. Geom. 58(2) 2017, 417–434.Google Scholar
McMullen, P., Nonlinear angle–sum relations for polyhedral cones and polytopes. Math. Proc. Cambridge Philos. Soc. 78 1975, 247–261.CrossRefGoogle Scholar
Padberg, M., Linear Optimization and Extensions, 2nd edn., Springer (Berlin, 1999).Google Scholar
Robinson, S. M., Normal maps induced by linear transformations. Math. Oper. Res. 17 1992, 691–714.Google Scholar
Lu, S. and Robinson, S. M., Normal fans of polyhedral convex sets. Structures and connections. Set-Valued Anal. 16 2008, 281–305.Google Scholar
Rockafellar, R. T., Convex Analysis, Princeton University Press (Princeton, NJ, 1970).Google Scholar
Scholtes, S., Introduction to Piecewise Differentiable Equations. Habilitationsschrift, Institut für Statistik und mathematische Wirtschaftstheorie, Universität Fridericiana Karlsruhe, Karlsruhe, Germany, 1994.Google Scholar
Scholtes, S., Introduction to Piecewise Differentiable Equations (Springer Briefs in Optimization), Springer (New York, 2012).CrossRefGoogle Scholar
Schneider, R., Combinatorial identities for polyhedral cones. Algebra i Analiz 29(1) 2017, 279–295.Google Scholar
Schneider, R., Convex Bodies: The Brunn-Minkowski Theory, 2nd edn., Cambridge University Press (Cambridge, 2014).Google Scholar
Schneider, R. and Weil, W., Stochastic and Integral Geometry, Springer (Heidelberg–New York, 2008).CrossRefGoogle Scholar
Ziegler, G. M., Lectures on Polytopes (Graduate Texts in Mathematics), Springer (New York, USA, 2007).Google Scholar