Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T17:16:04.594Z Has data issue: false hasContentIssue false
  • English
  • Français

An improvement to the Minkowski-Hiawka bound for packing superballs

Published online by Cambridge University Press:  26 February 2010

Jason A. Rush  and
N. J. A. Sloane
Jason A. Rush
Affiliation:
Department of Mathematics, University of California at San Diego, La Jolla, CA 92093, U.S.A.
N. J. A. Sloane
Affiliation:
Mathematical Sciences Research Center, AT & T Bell Laboratories, Murray Hill, NJ07974, U.S.A.
Get access

Abstract

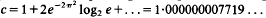The Minkowski-Hlawka bound implies that there exist lattice packings of n-dimensional “superballs” |x1|σ + … + |xn|σ ≤ 1 (σ = 1,2,…) having density Δ satisfying log2 Δ ≥ −n(l + o(l)) as n → ∞. For each n = pσ (p an odd prime) we exhibit a finite set of lattices, constructed from codes over GF(p), that contain packings of superballs having log2 Δ ≥ −cn(l + o(l)), where for σ = 2 (the classical sphere packing problem), worse than but surprisingly close to the Minkowski-Hlawka bound, and c = 0·8226 … for σ = 3, c = 0·6742 … for σ = 4, etc., improving on that bound.

Type
Research Article
Information
Mathematika , Volume 34 , Issue 1 , June 1987 , pp. 8 - 18
Copyright
Copyright © University College London 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bellman, R.. A Brief Introduction to Theta Functions (Holt, Rinehart and Winston, N.Y., 1961).Google Scholar
2.Berlekamp, E. R.. Algebraic Coding Theory (McGraw-Hill, N.Y., 1968).Google Scholar
3.de Bruijn, N. G.. Asymptotic Methods in Analysis (North-Holland, Amsterdam, 3rd edition, 1970).Google Scholar
4.Cassels, J. W. S.. An Introduction to the Geometry of Numbers (Springer-Verlag, N.Y., 2nd printing, 1971).Google Scholar
5.Conway, J. H. and Sloane, N. J. A.. Sphere Packings, Lattices and Groups (Springer-Verlag, N.Y., 1987, to appear).Google Scholar
6.Gardner, M.. Mathematical Carnival (Knopf, N.Y., 1975).Google Scholar
7.Kabatiansky, G. A. and Levenshtein, V. I.. Bounds for packings on a sphere and in space (in Russian), Problemy Peredachi Informatsii, 14 (No. 1, 1978), 3–25; English translation in Problems of Information Transmission, 14 (1978), 1–17.Google Scholar
8.Lee, C. Y.. Some properties of nonbinary error-correcting codes. IEEE Trans. Information Theory, IT-4 (1958), 77–82.CrossRefGoogle Scholar
9.Leech, J. and Sloane, N. J. A.. Sphere packing and error-correcting codes. Canad. J. Math., 23 (1971), 718–745.CrossRefGoogle Scholar
10.Lekkerkerker, C. G.. Geometry of Numbers (Wolters-Noordhoff, Groningen, 1969).Google Scholar
11.Litsin, S. N. and Tsfasman, M. A.. Algebraic-geometric and number-theoretic packings of spheres (in Russian). Uspekhi Mat. Nauk, 40 (1985), 185–186.Google Scholar
12.MacWilliams, F. J. and Sloane, N. J. A.. The Theory of Error-Correcting Codes (North-Holland, Amsterdam, 2nd printing, 1978).Google Scholar
13.Maher, D. P., Lee polynomials of codes and theta functions of lattices. Canad. J. Math., 30 (1978), 738–747.CrossRefGoogle Scholar
14.Rogers, C. A., Existence theorems in the Geometry of Numbers, Ann. Math., 48 (1947), 994–1002.CrossRefGoogle Scholar
15.Rogers, C. A., Packing and Covering (Cambridge Univ. Press, 1964).Google Scholar
16.Sloane, N. J. A., Self-dual codes and lattices. In Relations Between Combinatorics and Other Parts of Mathematics. Proc. Sympos. Pure Math., 34 (1979), 273–308.CrossRefGoogle Scholar
17.Sloane, N. J. A.. Recent bounds for codes, sphere packings and related problems obtained by linear programming and other methods. Contemp. Math., 9 (1982), 153–185.CrossRefGoogle Scholar
18.Whittaker, E. T. and Watson, G. N.. A Course of Modern Analysis (Cambridge Univ. Press, 4th ed., 1963).Google Scholar