No CrossRef data available.
Article contents
An Fσ semigroup of zero measure which contains a translate of every countable set
Part of:
Classical measure theory
Published online by Cambridge University Press: 26 February 2010
Extract
In 1942 Piccard [10] gave an example of a set of real numbers whose sum set has zero Lebesgue measure but whose difference set contains an interval. About thirty years later various authors (Connolly, Jackson, Williamson and Woodall) in a series of papers constructed F σ sets E in ℝ such that E – E contains an interval while the K-fold sum set
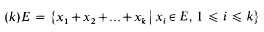
has zero Lebesgue measure for progressively larger values of k.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1984
References
1.Brown, G. and Moran, W.. Raikov systems and radicals in convolution measure algebras. J. London Math. Soc. (2), 28 (1983), 531–542.CrossRefGoogle Scholar
2.Cassels, J. W. S.. On a method of Marshall Hall. Mathematika, 3 (1956), 109–110.CrossRefGoogle Scholar
3.Connolly, D. M. and Williamson, J. H.. Difference-covers that are not k-sum covers II. Proc. Camb. Phil. Soc, 75 (1974), 63.CrossRefGoogle Scholar
4.Davenport, H.. A note on Diophantine Approximation. Studies in mathematical analysis and related topics (Stanford University Press, 1962), 77–81.Google Scholar
5.Gelfand, I. M., Raikov, D. A. and Shilov, G. E.. Commutative normed rings (New York, 1964).Google Scholar
6.Haight, J. A.. Difference covers which have small fσ-sums for any k. Mathematika, 20 (20), 20–20.Google Scholar
7.Hall, Marshall Jr. On the sum and product of continued fractions. Ann. of Math. (2), 48 (1947), 966–993.CrossRefGoogle Scholar
8.Hlavka, J. L.. Results on sums of continued fractions. Trans. Amer. Math. Soc, 211 (211), 211–211.Google Scholar
10.Piccard, S.. Sur des ensembles parfaits. Mém. Univ. Neuchâtel, vol. 16 (Secretariat de l'Universite, Neuchatel, 1942).Google Scholar


