Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T10:05:31.824Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXTENSION OF A THEOREM OF HLAWKA

Published online by Cambridge University Press:  29 April 2010

Martin Moskowitz  and
Richard Sacksteder
Martin Moskowitz
Affiliation:
Mathematics Ph.D. Program, The Graduate Center, City University of New York, New York, NY 10016, U.S.A. (email: [email protected])
Richard Sacksteder
Affiliation:
Mathematics Ph.D. Program, The Graduate Center, City University of New York, New York, NY 10016, U.S.A.
Get access

Abstract

This paper extends Hlawka’s theorem (from the point of view of Siegel and Weil) on SL(n,ℝ)/SL(n,ℤ) to Sp(n,ℝ)/Sp(n,ℤ). Namely, if Vn=vol(Sp(n,ℝ)/Sp(n,ℤ), where the measure is the Sp(n,ℝ)-invariant measure on Sp(n,ℝ)/Sp(n,ℤ), then Vn can be expressed in terms of the Riemann zeta function by 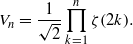As a consequence, let D be a domain of a sufficiently regular set in ℝ2n. Then:

  1. (i) if vol(D)>Vn, then some lattice in ℝ2n contains a non-zero point of D;

  2. (ii) if vol(D)<Vn, then some lattice in ℝ2n contains only the zero point of D;

  3. (iii) if D is star-shaped about the origin and vol(D)<ζ(2n)Vn, then some lattice in ℝ2n contains only the zero point of D.

At the same time, we also obtain unity with the “classical” SL(n,ℝ)/SL(n,ℤ) case.

Type
Research Article
Information
Mathematika , Volume 56 , Issue 2 , July 2010 , pp. 203 - 216
Copyright
Copyright © University College London 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Borel, A. and Harish-Chandra, , Arithmetic subgroups of algebraic groups. Ann. of Math. (2) 75 (1962), 485–535.CrossRefGoogle Scholar
[2]Chern, S. S., Integral geometry in Klein spaces. Ann. of Math. (2) 43 (1942), 180–189.CrossRefGoogle Scholar
[3]Halmos, P. R., Measure Theory, Van Nostrand (New York, 1950).CrossRefGoogle Scholar
[4]Hlawka, E., Zur Geometrie der Zahlen. Math. Z. 49 (1944), 270–277.Google Scholar
[5]Loomis, L. H., An Introduction to Abstract Harmonic Analysis, Van Nostrand (New York, 1953).Google Scholar
[6]Minkowski, H., Gesammelte Abhandlungen I, Teubner (Leipzig, 1911).Google Scholar
[7]Scharlau, W. and Opolka, H., From Fermat to Minkowski, Springer (Berlin, 1984).Google Scholar
[8]Siegel, C. L., A mean value theorem in the geometry of numbers. Ann. of Math. (2) 46 (1945), 340–347.CrossRefGoogle Scholar
[9]Stein, E. M. and Weiss, G., Fourier Analysis on Euclidean Spaces, Princeton University Press (Princeton, NJ, 1971).Google Scholar
[10]Weil, A., Sur quelques résults de Siegel. Summa Brasilienis Mathematicae 1 (1946), 21–39.Google Scholar
[11]Weil, A., L’intégration dans le groupes topologiques et ses applications, Hermann (Paris, 1965).Google Scholar
[12]Yosida, K., Functional Analysis, 6th edn., Springer (Berlin, 1980).Google Scholar