It is an empirical observation arising from the study of higher type computability that a wide range of approaches to defining a class of (hereditarily) total functionals over 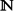 leads in practice to a relatively small handful of distinct type structures. Among these are the type structure C of Kleene–Kreisel continuous functionals, its effective substructure Ceff and the type structure HEO of the hereditarily effective operations. However, the proofs of the relevant equivalences are often non-trivial, and it is not immediately clear why these particular type structures should arise so ubiquitously.
leads in practice to a relatively small handful of distinct type structures. Among these are the type structure C of Kleene–Kreisel continuous functionals, its effective substructure Ceff and the type structure HEO of the hereditarily effective operations. However, the proofs of the relevant equivalences are often non-trivial, and it is not immediately clear why these particular type structures should arise so ubiquitously.
In this paper we present some new results that go some way towards explaining this phenomenon. Our results show that a large class of extensional collapse constructions always give rise to C, Ceff or HEO (as appropriate). We obtain versions of our results for both the ‘standard’ and ‘modified’ extensional collapse constructions. The proofs make essential use of a technique due to Normann.
Many new results, as well as some previously known ones, can be obtained as instances of our theorems, but more importantly, the proofs apply uniformly to a whole family of constructions, and provide strong evidence that the three type structures under consideration are highly canonical mathematical objects.


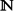 leads in practice to a relatively small handful of distinct type structures. Among these are the type structure C of Kleene–Kreisel
leads in practice to a relatively small handful of distinct type structures. Among these are the type structure C of Kleene–Kreisel