The differential λ-calculus is a paradigmatic functional programming language endowed with a syntactical differentiation operator that allows the application of a program to an argument in a linear way. One of the main features of this language is that it is resource conscious and gives the programmer suitable primitives to handle explicitly the resources used by a program during its execution. The differential operator also allows us to write the full Taylor expansion of a program. Through this expansion, every program can be decomposed into an infinite sum (representing non-deterministic choice) of ‘simpler’ programs that are strictly linear.
The aim of this paper is to develop an abstract ‘model theory’ for the untyped differential λ-calculus. In particular, we investigate what form a general categorical definition of a denotational model for this calculus should take. Starting from the work of Blute, Cockett and Seely on differential categories, we develop the notion of a Cartesian closed differential category and prove that linear reflexive objects living in such categories constitute sound and complete models of the untyped differential λ-calculus. We also give sufficient conditions for Cartesian closed differential categories to model the Taylor expansion. This requires that every model living in such categories equates all programs having the same full Taylor expansion.
We then provide a concrete example of a Cartesian closed differential category modelling the Taylor expansion, namely the category MRel of sets and relations from finite multisets to sets. We prove that the extensional model 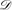 of λ-calculus we have recently built in MRel is linear, and is thus also an extensional model of the untyped differential λ-calculus. In the same category, we build a non-extensional model
of λ-calculus we have recently built in MRel is linear, and is thus also an extensional model of the untyped differential λ-calculus. In the same category, we build a non-extensional model 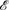 and prove that it is, nevertheless, extensional on its differential part.
and prove that it is, nevertheless, extensional on its differential part.
Finally, we study the relationship between the differential λ-calculus and the resource calculus, which is a functional programming language combining the ideas behind the differential λ-calculus with those behind Boudol's λ-calculus with multiplicities. We define two translation maps between these two calculi and study the properties of these translations. In particular, this analysis shows that the two calculi share the same notion of a model, and thus that the resource calculus can be interpreted by translation into every linear reflexive object living in a Cartesian closed differential category.
 fuzzy logic†
fuzzy logic†


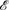
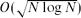 .
.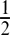 fuzzy logic
fuzzy logic