Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T23:26:19.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique decomposition of homogeneous languages and application to isothetic regions

Published online by Cambridge University Press:  10 October 2018

EMMANUEL HAUCOURT  and
NICOLAS NININ
EMMANUEL HAUCOURT
Affiliation:
LIX - UMR 7161, 1 rue Honoré d'Estienne d'Orves, Campus de l'École Polytechnique, Palaiseau 91120, France Email: [email protected]
NICOLAS NININ
Affiliation:
Laboratory for Topology and Neuroscience, Brain Mind Institute, EPFL, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A language is said to be homogeneous when all its words have the same length. Homogeneous languages thus form a monoid under concatenation. It becomes freely commutative under the simultaneous actions of every permutation group 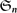on the collection of homogeneous languages of length n ∈ ℕ. One recovers the isothetic regions from (Haucourt 2017, to appear (online since October 2017)) by considering the alphabet of connected subsets of the space |G|, viz the geometric realization of a finite graph G. Factoring the geometric model of a conservative program amounts to parallelize it, and there exists an efficient factoring algorithm for isothetic regions. Yet, from the theoretical point of view, one wishes to go beyond the class of conservative programs, which implies relaxing the finiteness hypothesis on the graph G. Provided that the collections of n-dimensional isothetic regions over G (denoted by |G|) are co-unital distributive lattices, the prime decomposition of isothetic regions is given by an algorithm which is, unfortunately, very inefficient. Nevertheless, if the collections |G| satisfy the stronger property of being Boolean algebras, then the efficient factoring algorithm is available again. We relate the algebraic properties of the collections |G| to the geometric properties of the space |G|. On the way, the algebraic structure |G| is proven to be the universal tensor product, in the category of semilattices with zero, of n copies of the algebraic structure |G|.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 29 , Issue 5 , May 2019 , pp. 681 - 730
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, D.F. and Valdes-Leon, S. (1997). Factorization in commutative rings with zero divisors, II. In: Anderson, D. (ed.) Factorization in Integral Domains, Lecture Notes in Pure and Applied Mathematics, Marcel Dekker, New York, 197–219.Google Scholar
Allen, F.E. (1970). Control flow analysis. In: Proceedings of a Symposium on Compiler Optimization, ACM, New York, NY, USA, 1–19.Google Scholar
Balabonski, T. (2007). Concurrence, géométrie, et factorisation de catégories. Master's thesis, École Normale Supérieure de Lyon.Google Scholar
Balabonski, T. and Haucourt, E. (2010). A geometric approach to the problem of unique decomposition of processes. In: Concurrency Theory 21th International Conference, Lecture Notes in Computer Science, vol. 6269, Springer, 132–146.Google Scholar
Birkhoff, G. (1967). Lattice Theory, Colloquium Publications, vol. 25. American Mathematical Society, 3rd ed., Providence, Rhode Island, USA.Google Scholar
Borceux, F. (1994). Handbook of Categorical Algebra, II. Categories and Structures, Encyclopedia of Math. and its App., vol. 51, Cambridge University Press, Cambridge.Google Scholar
Bridson, M.R. and Haefliger, A. (1999). Metric Spaces of Non-Positive Curvature, Grundlehren der mathematischen Wissenschaften, vol. 319, Springer-Verlag, Berlin.Google Scholar
Brown, R. (2006). Topology and Groupoids, BookSurge Publishing.Google Scholar
Carson, S.D. and Reynolds, P. F. Jr. (1987). The geometry of semaphore programs. ACM Transactions on Programming Languages and Systems 9 (1) 25–53.Google Scholar
Coffman, E.G., Elphick, M. and Shoshani, A. (1971). System deadlocks. ACM Computing Surveys 3 (2) 67–78.Google Scholar
Cormen, T.H., Leiserson, C.E., Rivest, R.L. and Stein, C. (2009). Introduction to Algorithms, 3rd ed., MIT Press, USA.Google Scholar
Diestel, R. and Kühn, D. (2003). Graph-theoretical versus topological ends of graphs. Journal of Combinatorial Theory 87 (1) 197–206.Google Scholar
Dijkstra, E.W. (1965). Cooperating sequential processes. Technical report, Technological University, Eindhoven, The Netherlands, 1965. Reprinted in Genuys, F. Ed. 1968. Programming Languages, Academic Press, New York, 43–112. Article 1.Google Scholar
Fajstrup, L., Goubault, É. and Raußen, M. (2006). Algebraic topology and concurrency. Theoretical Computer Science 357 (1) 241–278.Google Scholar
Fajstrup, L., Goubault, É., Haucourt, E., Mimram, S. and Raußen, M. (2016). Directed Algebraic Topology and Concurrency, Springer, Switzerland.Google Scholar
Foertsch, T. and Lytchak, A. (2008). The de rham decomposition theorem for metric spaces. Geometric and Functional Analysis 18 120–143.Google Scholar
Fraser, G.A. (1976a). The semilattice tensor product of distributive lattices. Transactions of the American Mathematical Society 217 183–194.Google Scholar
Fraser, G.A. (1976b). Tensor products of semilattices and distributive lattices. Semigroup Forum 13 178–184.Google Scholar
Geroldinger, A. and Halter-Koch, F. (2006). Non-Unique Factorizations: Algebraic, Combinatorial, and Analytic Theory, Pure and Applied Mathematics, Chapman & Hall, Boca Raton, Florida, USA.Google Scholar
Givant, S. and Halmos, P. (2009). Introduction to Boolean Algebras, Undergraduate Texts in Mathematics, Springer, New York, USA.Google Scholar
Grandis, M. (2003). Directed homotopy theory, I. The fundamental category. Cahiers de Topologie et Géométrie Différentielle Catégoriques 44 (4) 281–316.Google Scholar
Grandis, M. (2009). Directed Algebraic Topology: Models of Non-Reversible Worlds, New Mathematical Monographs, vol. 13, Cambridge University Press, Cambridge.Google Scholar
Grillet, P. A. (1969a). The tensor product of semigroups. Transactions of the American Mathematical Society 138 267–280.Google Scholar
Grillet, P. A. (1969b). The tensor product of commutative semigroups. Transactions of the American Mathematical Society 138 281–293.Google Scholar
Hashimoto, J. (1951). On direct product decomposition of partially ordered sets. Annals of Mathematics 54 (2) 315–318.Google Scholar
Hatcher, A. (2002). Algebraic Topology. Cambridge University Press, Cambridge.Google Scholar
Haucourt, E. (2016). Some Invariants of Directed Topology Towards a Theoretical Base for a Static Analyzer Dealing with Fine-Grain Concurrency. Available on HAL.Google Scholar
Haucourt, E. (2017). The geometry of conservative programs. Mathematical Structures in Computer Science. Published online 17 October 2017. doi: 10.1017/S0960129517000226Google Scholar
Haucourt, E. and Ninin, N. (2014). The boolean algebra of cubical areas as a tensor product in the category of semilattices with zero. In: Proceedings of the 7th Interaction and Concurrency Experience, Electronic Proceedings in Theoretical Computer Science.Google Scholar
Hungerford, T.W. (2003). Algebra, Graduate Texts in Math., Springer-Verlag, New York.Google Scholar
Johnstone, P. T. (1982). Stone Spaces, Studies in Advanced Mathematics, vol. 3, Cambridge University Press, Cambridge.Google Scholar
Ketonen, J. (1978). The structure of countable boolean algebras. Annals of Mathematics 108 (1) 41–89.Google Scholar
Krishnan, S. (2009). A convenient category of locally preordered spaces. Applied Categorical Structures 17 (5) 445–466.Google Scholar
Lang, S. (2002). Algebra, Graduate Texts in Mathematics, 3rd ed., Springer, New York.Google Scholar
Munkres, J.R. (2000). Topology, 2nd ed., Prentice-Hall, USA.Google Scholar
Nadler, S.B. , S.B. Jr. (1992). Continuum Theory, An Introduction, Monographs and Textbooks in Pure and Applied Mathematics, vol. 158, Marcel Dekker, New York, USA.Google Scholar
Nakayama, T. and Hashimoto, J. (1950). On a problem of G. Birkoff. Proceeding of the American Mathematical Society 1 141–142.Google Scholar
Ninin, N. (2017). Factorisation des régions cubiques et applications à la concurrence. PhD thesis, Université Paris 11 Orsay.Google Scholar
Pierce, R.S. (1989). Countable Boolean algebras. In: Handbook of Boolean Algebras, vol. 3, Elsevier, Amsterdam, The Netherlands, 775–876.Google Scholar
Pratt, V. (2000). Higher dimensional automata revisited. Mathematical Structures in Computer Science 10 (4) 525–548.Google Scholar
Preparata, F.P. and Shamos, M.I. (1985). Computational Geometry: An Introduction. Texts and Monographs in Computer Science. Springer-Verlag, New York, 2nd printing.Google Scholar
Sikorski, R. (1950). The cartesian product of Boolean algeras. Fundamenta Matematicae 37 (1) 25–54.Google Scholar
van Glabbeek, R.J. (1991). Bisimulations for higher dimensional automata. Available at http://theory.stanford.edu/~rvg/hdaGoogle Scholar