No CrossRef data available.
Article contents
Some representations of real numbers using integer sequences
Published online by Cambridge University Press: 14 October 2022
Abstract
The paper describes three models of the real field based on subsets of the integer sequences. The three models are compared to the Harthong–Reeb line. Two of the new models, contrary to the Harthong–Reeb line, provide accurate integer “views” on real numbers at a sequence of growing scales
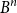 $B^n$
(
$B^n$
(
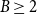 $B\ge2$
).
$B\ge2$
).
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Boldo, S., Lelay, C. and Melquiond, G. (2016). Formalization of real analysis: a survey of proof assistants and libraries. Mathematical Structures in Computer Science 26 (7) 1196–1233.CrossRefGoogle Scholar
Chollet, A. (2010). Non Classical Formalisms for the Computing Treatment of the Topology and the Discrete Geometry. PhD thesis, Université de La Rochelle.Google Scholar
Chollet, A., Wallet, G., Fuchs, L., Andres, E. and Largeteau-Skapin, G. (2012). Foundational aspects of multiscale digitization. Theoretical Computer Science 466 2–19.CrossRefGoogle Scholar
Chollet, A., Wallet, G., Fuchs, L., Largeteau-Skapin, G. and Andres, E. (2009). Insight in discrete geometry and computational content of a discrete model of the continuum. Pattern Recognition 42 (10) 2220–2228.CrossRefGoogle Scholar
Ciaffaglione, A. (2003). Certified Reasoning on Real Numbers and Objects in Co-Inductive Type Theory. Theses, Institut National Polytechnique de Lorraine.Google Scholar
Ciaffaglione, A. and Di Gianantonio, P. (2006). A certified, corecursive implementation of exact real numbers. Theoretical Computer Science 351 (1) 39–51.CrossRefGoogle Scholar
Da Col, M.-A. and Tellier, P. (2009). Quasi-linear transformations and discrete tilings. Theoretical Computer Science 410 2126–2134.CrossRefGoogle Scholar
Diener, F. and Reeb, G. (1989). Analyse Non Standard. Paris (France): <LQ_NY0CBJ>Hermann.Hermann.>Google Scholar
Harthong, J. (1989). Une théorie du continu. In: Les mathématiques non standard, 307–329.Google Scholar
Laugwitz, D. (1983).  $\Omega$-calculus as a generalization of field extension: an alternative approach to nonstandard analysis. In: Nonstandard Analysis - Recent developments, LNM, Springer, 120–133.Google Scholar
$\Omega$-calculus as a generalization of field extension: an alternative approach to nonstandard analysis. In: Nonstandard Analysis - Recent developments, LNM, Springer, 120–133.Google Scholar
Magaud, N., Chollet, A. and Fuchs, L. (2015). Formalizing a discrete model of the continuum in Coq from a discrete geometry perspective. Annals of Mathematics and Artificial Intelligence 74 (3–4) 309–332.CrossRefGoogle Scholar
Mazo, L. (2019). Multi-scale arithmetization of linear transformations. Journal of Mathematical Imaging and Vision 61 (4) 432–442.CrossRefGoogle Scholar
Ménissier-Morain, V. (1995). Arithmétique exacte: conception, algorithmique et performances d’une implémentation informatique en précision arbitraire. PhD thesis, Université Paris 7.Google Scholar
Ménissier-Morain, V. (2005). Arbitrary precision real arithmetic: design and algorithms. Journal of Logical and Algebraic Methods in Programming 64 (1) 13–39.CrossRefGoogle Scholar
Schmieden, C. and Laugwitz, D. (1958). Eine erweiterung der infinitesimalrechnung. Mathematische Zeitschrift 69 1–39.CrossRefGoogle Scholar



