Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T01:40:57.120Z Has data issue: false hasContentIssue false
  • English
  • Français

Rogers semilattices of punctual numberings

Published online by Cambridge University Press:  29 March 2022

Nikolay Bazhenov Open the ORCID record for Nikolay Bazhenov [Opens in a new window] ,
Manat Mustafa  and
Sergei Ospichev
Nikolay Bazhenov*
Affiliation:
Sobolev Institute of Mathematics, 4 Acad. Koptyug Avenue, Novosibirsk 630090, Russia
Manat Mustafa
Affiliation:
Department of Mathematics, School of Sciences and Humanities, Nazarbayev University, 53 Qabanbay Batyr Avenue, Nur-Sultan 010000, Kazakhstan
Sergei Ospichev
Affiliation:
Sobolev Institute of Mathematics, 4 Acad. Koptyug Avenue, Novosibirsk 630090, Russia
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper works within the framework of punctual computability, which is focused on eliminating unbounded search from constructions in algebra and infinite combinatorics. We study punctual numberings, that is, uniform computations for families S of primitive recursive functions. The punctual reducibility between numberings is induced by primitive recursive functions. This approach gives rise to upper semilattices of degrees, which are called Rogers pr-semilattices. We show that any infinite, uniformly primitive recursive family S induces an infinite Rogers pr-semilattice R. We prove that the semilattice R does not have minimal elements, and every nontrivial interval inside R contains an infinite antichain. In addition, every non-greatest element from R is a part of an infinite antichain. We show that the 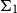$\Sigma_1$ -fragment of the theory Th(R) is decidable.

Keywords

Theory of numberingsupper semilatticeRogers semilatticeprimitive recursionFriedberg numberingdecidabilityonline computationpunctual structure
Type
Special Issue: Theory and Applications of Models of Computation (TAMC 2020)
Information
Mathematical Structures in Computer Science , Volume 32 , Issue 2: Theory and Applications of Models of Computation (TAMC 2020) , February 2022 , pp. 164 - 188
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badaev, S. and Goncharov, S. (2008). Computability and numberings. In: Cooper, S. B., Löwe, B. and Sorbi, A. (eds.) New Computational Paradigms, New York, Springer, 19–34.CrossRefGoogle Scholar
Badaev, S. A. and Goncharov, S. S. (2000). The theory of numberings: Open problems. In: Cholak, P., Lempp, S., Lerman, M. and Shore, R. (eds.) Computability Theory and Its Applications, Contemporary Mathematics, vol. 257, Providence, American Mathematical Society, 23–38.Google Scholar
Badaev, S. A., Goncharov, S. S. and Sorbi, A. (2006). Isomorphism types of Rogers semilattices for families from different levels of the arithmetical hierarchy. Algebra and Logic 45 (6) 361–370.CrossRefGoogle Scholar
Badaev, S. A. and Lempp, S. (2009). A decomposition of the Rogers semilattice of a family of d.c.e. sets. The Journal of Symbolic Logic 74 (2) 618–640.CrossRefGoogle Scholar
Bazhenov, N., Downey, R., Kalimullin, I. and Melnikov, A. (2019a). Foundations of online structure theory. The Bulletin of Symbolic Logic 25 (2) 141–181.CrossRefGoogle Scholar
Bazhenov, N., Harrison-Trainor, M., Kalimullin, I., Melnikov, A. and Ng, K. M. (2019b). Automatic and polynomial-time algebraic structures. The Journal of Symbolic Logic 84 (4) 1630–1669.CrossRefGoogle Scholar
Bazhenov, N., Mustafa, M. and Ospichev, S. (2020a). Semilattices of punctual numberings. In: Chen, J., Feng, Q. and Xu, J. (eds.) Theory and Applications of Models of Computation, Lecture Notes in Computer Science, vol. 12337, Cham, Springer, 1–12.Google Scholar
Bazhenov, N., Mustafa, M. and Yamaleev, M. (2019c). Elementary theories and hereditary undecidability for semilattices of numberings. Archive for Mathematical Logic 58 (3–4) 485–500.CrossRefGoogle Scholar
Bazhenov, N., Ospichev, S. and Yamaleev, M. (2019d). Isomorphism types of Rogers semilattices in the analytical hierarchy. Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore. To appear, preprint arXiv:1912.05226.Google Scholar
Bazhenov, N. A., Mustafa, M., Ospichev, S. S. and Yamaleev, M. M. (2020b). Numberings in the analytical hierarchy. Algebra and Logic 59 (5) 404–407.CrossRefGoogle Scholar
Cenzer, D. and Remmel, J. B. (1998). Complexity theoretic model theory and algebra. In: Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B. (eds.) Handbook of Recursive Mathematics, Vol. 1, Studies in Logic and the Foundations of Mathematics, vol. 138, Amsterdam, North-Holland, 381–513.Google Scholar
Dorzhieva, M. V. (2019). Computable numberings of families of infinite sets. Algebra and Logic 58 (3) 224–231.CrossRefGoogle Scholar
Downey, R., Greenberg, N., Melnikov, A., Ng, K. M. and Turetsky, D. (2020a). Punctual categoricity and universality. The Journal of Symbolic Logic 85 (4) 1427–1466.CrossRefGoogle Scholar
Downey, R., Harrison-Trainor, M., Kalimullin, I., Melnikov, A. and Turetsky, D. (2020b). Graphs are not universal for online computability. Journal of Computer and System Sciences 112 1–12.CrossRefGoogle Scholar
Downey, R., Melnikov, A. and Ng, K. M. (2021). Foundations of online structure theory II: The operator approach. Logical Methods in Computer Science 17 (3) 6:1–6:35.Google Scholar
Ershov, Y. L. (1967). Enumeration of families of general recursive functions. Siberian Mathematical Journal 8 (5) 771–778.CrossRefGoogle Scholar
Ershov, Y. L. (1977). Theory of Numberings, Moscow, Nauka. In Russian.Google Scholar
Ershov, Y. L. (1999). Theory of numberings. In: Griffor, E. R. (ed.) Handbook of Computability Theory , Studies in Logic and the Foundations of Mathematics, vol. 140, Amsterdam, North-Holland, 473–503.Google Scholar
Eršov, J. L. (1973). Theorie der Numerierungen I. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 19 (19–25) 289–388.CrossRefGoogle Scholar
Eršov, J. L. (1975). Theorie der Numerierungen II. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 21 (1) 473–584.CrossRefGoogle Scholar
Eršov, J. L. (1977). Theorie der Numerierungen III. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 23 (19–24) 289–371.Google Scholar
Goncharov, S. S., Lempp, S. and Solomon, D. R. (2002). Friedberg numberings of families of n-computably enumerable sets. Algebra and Logic 41 (2) 81–86.CrossRefGoogle Scholar
Goncharov, S. S. and Sorbi, A. (1997). Generalized computable numerations and nontrivial Rogers semilattices. Algebra and Logic 36 (6) 359–369.CrossRefGoogle Scholar
Herbert, I., Jain, S., Lempp, S., Mustafa, M. and Stephan, F. (2019). Reductions between types of numberings. Annals of Pure and Applied Logic 170 (12) 102716.CrossRefGoogle Scholar
Kalimullin, I., Melnikov, A. and Ng, K. M. (2017). Algebraic structures computable without delay. Theoretical Computer Science 674 73–98.CrossRefGoogle Scholar
Khutoretskii, A. B. (1971). On the cardinality of the upper semilattice of computable enumerations. Algebra and Logic 10 (5) 348–352.CrossRefGoogle Scholar
Kuznecov, A. V. (1950). On primitive recursive functions of large oscillation. Doklady Akademii Nauk SSSR 71 233–236. in Russian.Google Scholar
Mal’cev, A. I. (1965). Positive and negative numerations. Soviet Mathematics. Doklady 6 75–77.Google Scholar
Melnikov, A. G. (2017). Eliminating unbounded search in computable algebra. In: Kari, J., Manea, F. and Petre, I. (eds.) Unveiling Dynamics and Complexity, Lecture Notes in Computer Science, vol. 10307, Cham, Springer, 77–87.Google Scholar
Melnikov, A. G. and Ng, K. M. (2019). The back-and-forth method and computability without delay. Israel Journal of Mathematics 234 (2) 959–1000.CrossRefGoogle Scholar
Metakides, G. and Nerode, A. (1982). The introduction of nonrecursive methods into mathematics. In: The L. E. J. Brouwer Centenary Symposium (Noordwijkerhout, 1981), Studies in Logic and the Foundations of Mathematics, vol. 110, Amsterdam, North-Holland, 319–335.Google Scholar
Ospichev, S. S. (2015). Friedberg numberings in the Ershov hierarchy. Algebra and Logic 54 (4) 283–295.CrossRefGoogle Scholar
Paolini, L., Piccolo, M. and Roversi, L. (2016). A class of reversible primitive recursive functions. Electronic Notes in Theoretical Computer Science 322 227–242.CrossRefGoogle Scholar
Podzorov, S. Y. (2008). Arithmetical D-degrees. Siberian Mathematical Journal 49 (6) 1109–1123.CrossRefGoogle Scholar
Selivanov, V. L. (1976). Two theorems on computable numberings. Algebra and Logic 15 (4) 297–306.CrossRefGoogle Scholar