Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-22T14:59:28.880Z Has data issue: false hasContentIssue false
  • English
  • Français

Resource convertibility and ordered commutative monoids

Published online by Cambridge University Press:  12 October 2015

TOBIAS FRITZ
TOBIAS FRITZ*
Affiliation:
Perimeter Institute for Theoretical Physics, 31 Caroline St N, Waterloo, ON N2L 2Y5, Canada Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Resources and their use and consumption form a central part of our life. Many branches of science and engineering are concerned with the question of which given resource objects can be converted into which target resource objects. For example, information theory studies the conversion of a noisy communication channel instance into an exchange of information. Inspired by work in quantum information theory, we develop a general mathematical toolbox for this type of question. The convertibility of resources into other ones and the possibility of combining resources is accurately captured by the mathematics of ordered commutative monoids. As an intuitive example, we consider chemistry, where chemical reaction equations such as

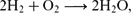\mathrm{2H_2 + O_2} \lra \mathrm{2H_2O,}
are concerned both with a convertibility relation ‘→’ and a combination operation ‘+.’ We study ordered commutative monoids from an algebraic and functional-analytic perspective and derive a wealth of results which should have applications to concrete resource theories, such as a formula for rates of conversion. As a running example showing that ordered commutative monoids are also of purely mathematical interest without the resource-theoretic interpretation, we exemplify our results with the ordered commutative monoid of graphs.

While closely related to both Girard's linear logic and to Deutsch's constructor theory, our framework also produces results very reminiscent of the utility theorem of von Neumann and Morgenstern in decision theory and of a theorem of Lieb and Yngvason on the foundations of thermodynamics.

Concerning pure algebra, our observation is that some pieces of algebra can be developed in a context in which equality is not necessarily symmetric, i.e. in which the equality relation is replaced by an ordering relation. For example, notions like cancellativity or torsion-freeness are still sensible and very natural concepts in our ordered setting.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Issue 6 , September 2017 , pp. 850 - 938
Copyright
Copyright © Cambridge University Press 2015 

References

Abeyesinghe, A., Devetak, I., Hayden, P. and Winter, A. (2009). The mother of all protocols: Restructuring quantum information's family tree. Proceedings of the Royal Society A 465 (2108) 2537–2563.CrossRefGoogle Scholar
Adámek, J., Herrlich, H. and Strecker, G.E. (1990). Abstract and Concrete Categories: The joy of cats, Pure and Applied Mathematics, New York, John Wiley & Sons, Wiley-Interscience Publication. Inc. Available at: tac.mta.ca/tac/reprints/articles/17/tr17abs.html.Google Scholar
Aliprantis, C.D. and Tourky, R. (2007). Cones and Duality, Graduate Studies in Mathematics, volume 84, American Mathematical Society.CrossRefGoogle Scholar
Aubrun, G. and Nechita, I. (2008). Catalytic majorization and ℓ p norms. Communications in Mathematical Physics 278 (1) 133–144.CrossRefGoogle Scholar
Bennett, C.H. (1998). Quantum information. Physica Scripta T76 210–217.CrossRefGoogle Scholar
Bennett, C.H., Bernstein, H.J., Popescu, S. and Schumacher, B. (1996a). Concentrating partial entanglement by local operations. Physical Review A 53 (4) 2046–2052.CrossRefGoogle ScholarPubMed
Bennett, C.H., Brassard, G., Popescu, S., Schumacher, B., Smolin, J.A. and Wootters, W.K. (1996b). Purification of noisy entanglement and faithful teleportation via noisy channels. Physical Review Letters 76 (5) 722–725.CrossRefGoogle ScholarPubMed
Bennett, C.H., Devetak, I., Harrow, A.W., Shor, P.W. and Winter, A. (2014). The quantum reverse shannon theorem and resource tradeoffs for simulating quantum channels. IEEE Transactions on Information Theory 60 (5) 2926–2959.CrossRefGoogle Scholar
Blackadar, B. (1998). K-Theory for Operator Algebras, Mathematical Sciences Research Institute Publications, volume 5, 2nd edition, Cambridge, Cambridge University Press.Google Scholar
Blackadar, B. and Rørdam, M. (1992). Extending states on preordered semigroups and the existence of quasitraces on C*-algebras. Journal of Algebra 152 (1) 240–247.CrossRefGoogle Scholar
Brandão, F.G.S.L. and Gour, G. (2015). Reversible framework for quantum resource theories. Physical Review Letters 115 070503.Google ScholarPubMed
Brandão, F.G.S.L., Horodecki, M., Ng, N. Oppenheim, J. and Wehner, S. (2013). The second laws of quantum thermodynamics. Proceedings of the National Academy of Sciences of the United States of America 112 (11) 3275–3279.CrossRefGoogle Scholar
Brandão, F.G.S.L., Horodecki, M., Oppenheim, J., Renes, J.M. and Spekkens, R.W. (2013a). Resource theory of quantum states out of thermal equilibrium. Physical Review Letters 111 250404.CrossRefGoogle Scholar
Brandom, R. (2000). Articulating Reasons, Harvard University Press.CrossRefGoogle Scholar
Chudnovsky, M., Robertson, N., Seymour, P. and Thomas, R. (2006). The strong perfect graph theorem. Annals of Mathematics 164 (1) 51–229.CrossRefGoogle Scholar
Cimprič, J., Marshall, M. and Netzer, T. (2011). Closures of quadratic modules. Israel Journal of Mathematics 183 (1) 445–474.CrossRefGoogle Scholar
Coecke, B., Fritz, T. and Spekkens, R. W. (2014). A mathematical theory of resources. arXiv:1409.5531.Google Scholar
Cubitt, T., Mančinska, L., Roberson, D., Severini, S., Stahlke, D. and Winter, A. (2014). Bounds on entanglement assisted source-channel coding via the lovasz theta number and its variants. IEEE Transactions on Information Theory 60 (11) 7330–7344.CrossRefGoogle Scholar
Cubitt, T.S., Leung, D., Matthews, W. and Winter, A. (2011). Zero-error channel capacity and simulation assisted by non-local correlations. IEEE Transactions on Information Theory 57 (8) 5509–5523.CrossRefGoogle Scholar
Darnel, M.R. (1995). Theory of Lattice-Ordered Groups, Monographs and Textbooks in Pure and Applied Mathematics, volume 187, New York, Marcel Dekker Inc.Google Scholar
Datta, N. and Hsieh, M.-H. (2011). The apex of the family tree of protocols: Optimal rates and resource inequalities. New Journal of Physics 13 093042.CrossRefGoogle Scholar
Deutsch, D. (2013). Constructor theory. Synthese 190 (18) 4331–4359.CrossRefGoogle Scholar
Deutsch, D. and Marletto, C. (2014). Constructor theory of information. arXiv:1405.5563.Google Scholar
Devetak, I., Harrow, A.W. and Winter, A. (2008). A resource framework for quantum Shannon theory. IEEE Transactions on Information Theory 54 (10) 4587–4618.CrossRefGoogle Scholar
Di Cosmo, R. and Miller, D. (2006–2015). Linear logic. In: Zalta, E.N. (ed.) The Stanford Encyclopedia of Philosophy. The Metaphysics Research Lab, Stanford University. Available at: http://plato.stanford.edu/archives/sum2015/entries/logic-linear/.Google Scholar
Duan, R., Feng, Y., Li, X. and Ying, M. (2005). Multiple-copy entanglement transformation and entanglement catalysis. Physical Review A 71 042319. Available at: http://arxiv.org/abs/quant-ph/0404148.CrossRefGoogle Scholar
Engler, J.-O. and Baumgärtner, S. (2013). An Axiomatic Approach to Decision under Knightian Uncertainty. Available at: eea-esem.com/eea-esem/2013/prog/viewpaper.asp?pid=1914.Google Scholar
Fakhruddin, S.M. (1986). Absolute flatness and amalgams in pomonoids. Semigroup Forum 33 (1) 15–22.CrossRefGoogle Scholar
Feinberg, M. and Lavine, R. (1983). Thermodynamics based on the Hahn–Banach theorem: The Clausius inequality. Archive for Rational Mechanics and Analysis 82 (3) 203–293.CrossRefGoogle Scholar
Fritz, T. (2009). Possibilistic Physics. Available at: fqxi.org/community/forum/topic/569.Google Scholar
Fuchssteiner, B. and Lusky, W. (1981). Convex Cones, North-Holland Mathematics Studies, volume 56, Amsterdam-New York, North-Holland Publishing Co.Google Scholar
Girard, J.-Y. (1987). Linear logic. Theoretical Computer Science 50 (1) 101.CrossRefGoogle Scholar
Glass, A.M.W. (1999) Partially Ordered Groups, Series in Algebra, volume 7, River Edge, NJ, World Scientific Publishing Co., Inc.CrossRefGoogle Scholar
Godsil, C., Roberson, D. W., Šámal, R. and Severini, S. (2015). Sabidussi versus Hedetniemi for three variations of the chromatic number. Combinatorica. Available at: http://link.springer.com/article/10.1007%2Fs00493-014-3132-1.Google Scholar
Golan, J.S. (1999). Semirings and Their Applications, Dordrecht, Kluwer Academic Publishers. Updated and expanded version of The Theory of Semirings, with Applications to Mathematics and Theoretical Computer Science [Harlow, Longman Sci. Tech., 1992].CrossRefGoogle Scholar
Goodearl, K.R. (1986). Partially Ordered Abelian Groups with Interpolation, Mathematical Surveys and Monographs, volume 20, Providence, RI, American Mathematical Society.Google Scholar
Gour, G., Müller, M.P., Narasimhachar, V., Spekkens, R.W. and Halpern, N.Y. (2013). The resource theory of informational nonequilibrium in thermodynamics. Physics Reports 583 1–58.CrossRefGoogle Scholar
Gour, G. and Spekkens, R.W. (2008). The resource theory of quantum reference frames: Manipulations and monotones. New Journal of Physics 10 033023.CrossRefGoogle Scholar
Grillet, P.A. (2001). Commutative Semigroups, Advances in Mathematics, volume 2, Dordrecht, Kluwer Academic Publishers.CrossRefGoogle Scholar
Halpern, N.Y. (2014). Beyond heat baths II: Framework for generalized thermodynamic resource theories. arXiv:1409.7845.Google Scholar
Halpern, N.Y. and Renes, J.M. (2014). Beyond heat baths: Generalized resource theories for small-scale thermodynamics. arXiv:1409.3998.Google Scholar
Harrow, A.W. (2010). Entanglement spread and clean resource inequalities. In: Proceedings of the 16th International Congress on Mathematical Physics, World Scientific, 536–540.CrossRefGoogle Scholar
Horodecki, M., Horodecki, P. and Oppenheim, J. (2003). Reversible transformations from pure to mixed states, and the unique measure of information. Physical Review A 67 062104.CrossRefGoogle Scholar
Horodecki, M. and Oppenheim, J. (2013). (Quantumness in the context of) resource theories. International Journal of Modern Physics B 27 1345019.CrossRefGoogle Scholar
Horodecki, R., Horodecki, P., Horodecki, M. and Horodecki, K. (2009). Quantum entanglement. Reviews of Modern Physics 81 (2) 865–942.CrossRefGoogle Scholar
Howe, E. (1986). A new proof of Erdős' theorem on monotone multiplicative functions. American Mathematical Monthly 93 (8) 593–595.Google Scholar
Hsieh, M.-H. and Wilde, M. (2010a). Entanglement-assisted communication of classical and quantum information. IEEE Transactions on Information Theory 56 (9) 4682–4704.CrossRefGoogle Scholar
Hsieh, M.-H. and Wilde, M. (2010b). Trading classical communication, quantum communication, and entanglement in quantum shannon theory. IEEE Transactions on Information Theory 56 (9) 4705–4730.CrossRefGoogle Scholar
Imrich, W. and Klavžar, S. (2000). Product Graphs, Structure and Recognition, Wiley-Interscience Series in Discrete Mathematics and Optimization. New York, Wiley-Interscience.Google Scholar
Janzing, D., Wocjan, P., Zeier, R., Geiss, R. and Beth, T. (2000). The thermodynamic cost of reliability and low temperatures: Tightening Landauer's principle and the second law. International Journal of Theoretical Physics 39 (12) 2217–2753.CrossRefGoogle Scholar
Joyal, A., Street, R. and Verity, D. (1996). Traced monoidal categories. Mathematical Proceedings of the Cambridge Philosophical Society 119 (3) 447–468.CrossRefGoogle Scholar
Karoubi, M. (1978). K-Theory, Berlin-New York, Springer-Verlag. An introduction, Grundlehren der Mathematischen Wissenschaften, Band 226.CrossRefGoogle Scholar
Kehayopulu, N. and Tsingelis, M. (1998). On separative ordered semigroups. Semigroup Forum 56 (2) 187–196.CrossRefGoogle Scholar
Kelley, J.L. and Namioka, I. (1976). Linear Topological Spaces, Graduate Texts in Mathematics, volume 36, Springer-Verlag, New York-Heidelberg.Google Scholar
Kelly, G.M. (2005). Basic concepts of enriched category theory. Reprints Theory and Applications of Categories 10 vi+137. Reprint of the 1982 original. Available at: tac.mta.ca/tac/reprints/articles/10/tr10abs.html.Google Scholar
Klimesh, M. (2007). Inequalities that collectively completely characterize the catalytic majorization relation. arXiv:0709.3680.Google Scholar
Knuth, D.E. (1994). The sandwich theorem. Electronic Journal of Combinatorics 1 A1.CrossRefGoogle Scholar
Kock, J. (2004). Frobenius Algebras and 2D Topological Quantum Field Theories, London Mathematical Society Student Texts, volume 59, Cambridge, Cambridge University Press.Google Scholar
Kreps, D.M. (1988). Notes on the Theory of Choice, Westview Press.Google Scholar
Lawvere, F.W. (2002). Metric spaces, generalized logic, and closed categories [Rend. Sem. Mat. Fis. Milano 43 (1973), 135–166 (1974)]. Repr. Theory Applications of Categories 1 1–37. With an author commentary: Enriched categories in the logic of geometry and analysis. Available at: tac.mta.ca/tac/reprints/articles/1/tr1abs.html.Google Scholar
Leinster, T. (2014). Basic Category Theory, Cambridge University Press.CrossRefGoogle Scholar
Lieb, E.H. and Yngvason, J. (1998). A guide to entropy and the second law of thermodynamics. Notices Amer. Math. Soc. 45 571–581.Google Scholar
Lieb, E.H. and Yngvason, J. (1999). The physics and mathematics of the second law of thermodynamics. Physics Reports 310 1–96.CrossRefGoogle Scholar
Lieb, E.H. and Yngvason, J. (2000). A fresh look at entropy and the second law of thermodynamics. Physics Today 53 (4) 32–37.CrossRefGoogle Scholar
Lieb, E.H. and Yngvason, J. (2002). The mathematical structure of the second law of thermodynamics. In: Current Developments in Mathematics, 2001, Int. Press, Somerville, MA, 89–129.Google Scholar
Lieb, E.H. and Yngvason, J. (2014). Entropy meters and the entropy of non-extensive systems. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science 470 (2167) 20140192.CrossRefGoogle ScholarPubMed
Lovász, L. (1979). On the Shannon capacity of a graph. IEEE Transactions on Information Theory 25 (1) 1–7. Available at: cs.elte.hu/~lovasz/scans/theta.pdf.CrossRefGoogle Scholar
Luttik, B. (2003). A unique decomposition theorem for ordered monoids with applications in process theory (extended abstract). In: Mathematical Foundations of Computer Science 2003, Lecture Notes in Computer Science volume 2747, Springer, Berlin, 562–571. Available at: win.tue.nl/~luttik/Papers/Udecomp.pdf.CrossRefGoogle Scholar
Marletto, C. (2015). The constructor theory of life. Royal Society Interface 12 (104) arXiv:1407.0681.Google ScholarPubMed
Marshall, A.W. and Olkin, I. (1979). Inequalities: Theory of Majorization and its Applications, Mathematics in Science and Engineering, volume 143, Academic Press, Inc.Google Scholar
Marvian, I. and Spekkens, R.W. (2013). The theory of manipulations of pure state asymmetry: Basic tools and equivalence classes of states under symmetric operations. New Journal of Physics 15 033001.CrossRefGoogle Scholar
Marvian, I. and Spekkens, R.W. (2014). Modes of asymmetry: The application of harmonic analysis to symmetric quantum dynamics and quantum reference frames. Physical Review A 90 062110.CrossRefGoogle Scholar
Moreira Dos Santos, C. Decomposition of strongly separative monoids. Journal of Pure and Applied Algebra 172 (1) 25–47.CrossRefGoogle Scholar
Nakada, O. (1951). Partially ordered Abelian semigroups. I. On the extension of the strong partial order defined on Abelian semigroups. Journal of the Faculty of Science, Hokkaido University. Series I. 11 181–189.Google Scholar
Nielsen, M.A. (1999). Conditions for a class of entanglement transformations. Physical Review Letters 83 436.CrossRefGoogle Scholar
nLab. Stuff, structure, property, (2014). Available at: ncatlab.org/nlab/revision/stuff,+structure,+property/38.Google Scholar
Paulsen, V. and Tomforde, M. (2009). Vector spaces with an order unit. Indiana University Mathematics Journal 3 1319–1359.CrossRefGoogle Scholar
Pultr, A. and Trnková, V. (1980). Combinatorial, Algebraic and Topological Representations of Groups, Semigroups and Categories, North-Holland Mathematical Library, volume 22, Amsterdam-New York, North-Holland Publishing Co.Google Scholar
Raftery, J.G. and van Alten, C.J. (2000). Residuation in commutative ordered monoids with minimal zero. Reports on Mathematical Logic 34 23–57. Algebra & substructural logics (Tatsunokuchi, 1999). Available at: http://rml.tcs.uj.edu.pl/rml-34/cont-34.htm.Google Scholar
Roberson, D.E. (2013). Variations on a Theme: Graph Homomorphisms. PhD thesis, University of Waterloo. Available at: uwspace.uwaterloo.ca/handle/10012/7814.Google Scholar
Roberson, D.E. and Mančinska, L. (2012). Graph homomorphisms for quantum players. In: Proceedings of the 9th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2014) 212–216.Google Scholar
Rørdam, M., Larsen, F. and Laustsen, N. (2000) An Introduction to K-Theory for C*-Algebras, London Mathematical Society Student Texts, volume 49, Cambridge, Cambridge University Press. See also math.ku.dk/~rordam/K-theory.html.CrossRefGoogle Scholar
Rosales, J.C. and García-Sánchez, P.A. (2009). Numerical Semigroups, Developments in Mathematics, volume 20, New York, Springer.CrossRefGoogle Scholar
Rosenthal, K.I. (1990). Quantales and their Applications, Pitman Research Notes in Mathematics Series, volume 234, New York, Longman Scientific & Technical, Harlow; copublished in the United States with John Wiley & Sons, Inc.Google Scholar
Schaefer, H.H. and Wolff, M.P. (1999). Topological Vector Spaces, Graduate Texts in Mathematics, volume 3, 2nd edition, New York, Springer-Verlag.CrossRefGoogle Scholar
Scheinerman, E.R. and Ullman, D.H. (2011). Fractional Graph Theory, Mineola, NY, Dover Publications, Inc. A rational approach to the theory of graphs, With a foreword by Claude Berge, Reprint of the 1997 original.Google Scholar
Shannon, C.E. (1948). A mathematical theory of communication. Bell System Technical Journal 27 379–423, 623–656. Available at: cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf.CrossRefGoogle Scholar
Shannon, C.E. (1956). The zero error capacity of a noisy channel. IRE Transactions on Information Theory 2 (3) 8–19.CrossRefGoogle Scholar
Shirahata, M. (1996). A Sequent Calculus for Compact Closed Categories. Available at: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.57.3906.Google Scholar
Thess, A. (2011). The Entropy Principle. Thermodynamics for the Unsatisfied, Springer.Google Scholar
Tsinakis, C. and Zhang, H. (2004). Order algebras as models of linear logic. Studia Logica 76 (2) 201–225. Available at: my.vanderbilt.edu/constantinetsinakis/files/2014/03/petri.pdf.CrossRefGoogle Scholar
Vidal, G. (2000). Entanglement monotones. Journal of Modern Optics 47 355–376.CrossRefGoogle Scholar
von Neumann, J. and Morgenstern, O. (2007). Theory of Games and Economic Behavior, Princeton, NJ, Princeton University Press, anniversary edition. With an introduction by Harold W. Kuhn and an afterword by Ariel Rubinstein.Google Scholar
Wehrung, F. (1992). Injective positively ordered monoids. I, II. Journal of Pure and Applied Algebra 83 (1) 43–100.CrossRefGoogle Scholar
World Wide Web Consortium. (2006). The rule of least power. Available at: w3.org/2001/tag/doc/leastPower.html.Google Scholar