Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-22T20:56:59.679Z Has data issue: false hasContentIssue false
  • English
  • Français

On the computational complexity of the Dirichlet Problem for Poisson's Equation

Published online by Cambridge University Press:  28 July 2016

AKITOSHI KAWAMURA ,
FLORIAN STEINBERG  and
MARTIN ZIEGLER
AKITOSHI KAWAMURA
Affiliation:
Graduate School of Arts and Sciences, University of Tokyo, Tokyo, Japan
FLORIAN STEINBERG
Affiliation:
Graduate School of Arts and Sciences, University of Tokyo, Tokyo, Japan Department of Mathematics, TU Darmstadt, Darmstadt, Germany
MARTIN ZIEGLER
Affiliation:
Department of Mathematics, TU Darmstadt, Darmstadt, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

The last years have seen an increasing interest in classifying (existence claims in) classical mathematical theorems according to their strength. We pursue this goal from the refined perspective of computational complexity. Specifically, we establish that rigorously solving the Dirichlet Problem for Poisson's Equation is in a precise sense ‘complete’ for the complexity class 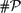${\#\mathcal{P}}$ and thus as hard or easy as parametric Riemann integration (Friedman 1984; Ko 1991. Complexity Theory of Real Functions).

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 27 , Special Issue 8: Continuity, Computability, Constructivity: From Logic to Algorithms 2013 , December 2017 , pp. 1437 - 1465
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blumenson, L.E. (1960). Classroom notes: A derivation of n-Dimensional spherical coordinates. The American Mathematical Monthly 67 (1) 63–66.Google Scholar
Bournez, O., Graça, D.S., Pouly, A. and Zhong, N. (2013). Computability and computational complexity of the evolution of nonlinear dynamical systems. In: Proc. 9th Conference on Computability in Europe (CiE 2013), Springer LNCS vol. 7921, doi 10.1007/978-3-642-39053-1_2.Google Scholar
Brattka, V. and Yoshikawa, A. (2006). Towards computability of elliptic boundary value problems in variational formulation. Journal of Complexity, 22 858–880.CrossRefGoogle Scholar
Braverman, M. (2005). On the complexity of real functions. In: Proc. 6th Annual IEEE Symposium on Foundations of Computer Science, doi 10.1109/SFCS.2005.58.Google Scholar
Friedman, H. (1984). The computational complexity of maximization and integration. Advances in Mathematics 53 (1) 80–98.CrossRefGoogle Scholar
Garey, M.R. and Johnson, D.S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness, Freeman, New York.Google Scholar
Gilbarg, D. and Trudinger, N.S. (2001). Elliptic Partial Differential Equations of Second Order, Classics in Mathematics. Springer-Verlag, Berlin. Reprint of the 1998 edition.CrossRefGoogle Scholar
Grzegorczyk, A. (1957). On the definitions of computable real continuous functions. Fundamenta Mathematicae 44 61–71.CrossRefGoogle Scholar
Kawamura, A. (2010). Lipschitz continuous ordinary differential equations are polynomial-space complete. Computational Complexity 19 (2) 305–332.CrossRefGoogle Scholar
Kawamura, A. (2011). Computational Complexity in Analysis and Geometry. PhD thesis, University of Toronto.Google Scholar
Kawamura, A. and Cook, S. (2012). Complexity theory for operators in analysis. ACM Transactions in Computation Theory 4 (2) Article 5.CrossRefGoogle Scholar
Kawamura, A., Ota, H., Rösnick, C. and Ziegler, M. (2014). Computational complexity of smooth differential equations. Logical Methods in Computer Science 10 (1) 6.Google Scholar
Ko, K.-I. (1982). The maximum value problem and NP real numbers. Journal of Computer and System Sciences 24 (1) 15–35.CrossRefGoogle Scholar
Ko, K.-I. (1990). Inverting a one-to-one real function is inherently sequential. In: Feasible Mathematics (Ithaca, NY, 1989), Progress in Computer Science and Applied Logic, volume 9, Birkhäuser Boston, Boston, MA 239–257.CrossRefGoogle Scholar
Ko, K.-I. (1991). Complexity Theory of Real Functions. Progress in Theoretical Computer Science. Birkhäuser Boston Inc., Boston, MA.CrossRefGoogle Scholar
Ko, K.-I. (1992). On the computational complexity of integral equations. Annals of Pure and Applied Logic 53 (3) 201–228.CrossRefGoogle Scholar
Ko, K.-I. (1998). Polynomial-time computability in analysis. In: Handbook of Recursive Mathematics, Vol. 2, Studies in Logic and the Foundations of Mathematics, volume 139, North-Holland, Amsterdam 1271–1317.Google Scholar
Ko, K.-I. and Friedman, H. (1982). Computational complexity of real functions. Theoretical Computer Sciences 20 (3), 323–352.CrossRefGoogle Scholar
Ko, K.-I. and Yu, F. (2008). On the complexity of convex hulls of subsets of the two-dimensional plane. In: Proceedings of the 4th International Conference on Computability and Complexity in Analysis (CCA 2007). Electron. Notes Theor. Comput. Sci. 202 Elsevier Sci. B. V., Amsterdam 121–135.Google Scholar
Labhalla, S., Lombardi, H. and Moutai, E. (2001). Espaces métriques rationnellement présentés et complexité. Theoretical Computer Science 250 265–332. le cas de l'espace des fonctions réelles uniformément, continues sur un intervalle compact.CrossRefGoogle Scholar
Lacombe, D. (1958). Sur les possibilités d'extension de la notion de fonction récursive aux fonctions d'une ou plusieurs variables réelles. In: Le raisonnement en mathématiques et en sciences expérimentales, Colloques Internationaux du Centre National de la Recherche Scientifique, LXX, Editions du Centre National de la Recherche Scientifique, Paris 67–75.Google Scholar
Morera, G. (1887). Sulle derivate seconde della funzione potenziale di spazio. Rendiconti 20 302–310.Google Scholar
Müller, N.T. (1987). Uniform computational complexity of Taylor series. In: Proceeding 14th International Colloquium on Automata, Languages, and Programming. Springer-Verlag Lecture Notes in Computer Science 267 435–444.Google Scholar
Müller, N.T. (1995). Constructive aspects of analytic functions. In: Proc. Workshop on Computability and Complexity in Analysis, volume 190 of InformatikBerichte, FernUniversität Hagen 105–114.Google Scholar
Parberry, I. and Schnitger, G. (1988). Parallel computation with threshold functions. Journal of Computer and System Sciences 36 278–302.CrossRefGoogle Scholar
Pour-El, M.B. and Richards, J.I. (1989). Computability in Analysis and Physics, Perspectives in Mathematical Logic, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Rösnick, C. (2013). Closed sets and operators thereon: Representations, computability and complexity. In: Proceedings of the 10th International Conference on Computability and Complexity in Analysis (CCA), 8-10 July 2013, Nancy, France.Google Scholar
Sun, S., Zhong, N. and Ziegler, M. (2015). Computability of navier-stokes' equation. In: Proceeding of the 11th Conference on Computability in Europe, Lecture Notes in Computer Science 9136 334–342.Google Scholar
Toda, S. (1991). PP is as hard as the polynomial-time hierarchy. SIAM Journal on Computing 20 (5) 865–877.CrossRefGoogle Scholar
Turing, A. (1936). On computable numbers, with an application to the Entscheidungsproblem. Proceedings of the London Mathematical Society 42 (2) 230–265.Google Scholar
Weihrauch, K. (2000). Computable Analysis . An Introduction. Springer, Berlin/Heidelberg.Google Scholar
Weihrauch, K. and Zhong, N. (2002). Is wave propagation computable or can wave computers beat the Turing machine?. Proceedings of London Mathematical Society 85 (2) 312–332.CrossRefGoogle Scholar
Weihrauch, K. and Zhong, N. (2005). Computing the solution of the Korteweg–de Vries equation with arbitrary precision on turing. Theoretical Computer Science 332 (1–3) 337–366.CrossRefGoogle Scholar
Weihrauch, K. and Zhong, N. (2006). An algorithm for computing fundamental solutions. SIAM Journal on Computing 35 (6) 1283–1294.CrossRefGoogle Scholar
Weihrauch, K. and Zhong, N. (2007). Computable analysis of the abstract Cauchy problem in a Banach space and its applications I. Mathematical Logic Quarterly 53 (4–5) 511–531.CrossRefGoogle Scholar
Wienholtz, E., Kalf, H. and Kriecherbauer, T. (2009). Elliptische Differentialgleichungen zweiter Ordnung. Springer, Dordrecht. Eine Einführung mit historischen Bemerkungen. [An introduction with historical remarks].CrossRefGoogle Scholar
Zhong, N. (1998). Derivatives of computable functions. Mathematical Logic Quarterly 44 304–316.CrossRefGoogle Scholar