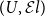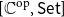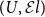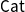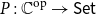Let
![]() $\widehat{{\mathbb{C}}} ={[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]}$
be the category of presheaves on the small category
$\widehat{{\mathbb{C}}} ={[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]}$
be the category of presheaves on the small category
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
1. The Hofmann–Streicher Universe
In Hofmann and Streicher (Reference Hofmann and Streicher1997), the authors define a (type-theoretic) universe
![]() $(U,{\mathcal{E}l})$
with
$(U,{\mathcal{E}l})$
with
![]() $U\in \widehat{{\mathbb{C}}}$
and
$U\in \widehat{{\mathbb{C}}}$
and
![]() ${\mathcal{E}l} \in \widehat{\int _{\mathbb{C}} U}$
as follows. For
${\mathcal{E}l} \in \widehat{\int _{\mathbb{C}} U}$
as follows. For
![]() $I\in{\mathbb{C}}$
and
$I\in{\mathbb{C}}$
and
![]() $A :{{({\mathbb{C}}/_I)}^{\textrm{op}}} \rightarrow{\textsf{Set}}$
, let
$A :{{({\mathbb{C}}/_I)}^{\textrm{op}}} \rightarrow{\textsf{Set}}$
, let
with an evidently associated action on morphisms. A few comments are required:
-
1. In (1), we have taken the underlying set of objects of the category
 $\widehat{{\mathbb{C}}/_I}={[{{{\mathbb{C}}/_I}^{\textrm{op}}},\textsf{Set}]}$
(in contrast to the specification in Hofmann and Streicher (Reference Hofmann and Streicher1997)).
$\widehat{{\mathbb{C}}/_I}={[{{{\mathbb{C}}/_I}^{\textrm{op}}},\textsf{Set}]}$
(in contrast to the specification in Hofmann and Streicher (Reference Hofmann and Streicher1997)). -
2. In (2), and throughout Hofmann and Streicher (Reference Hofmann and Streicher1997), the authors steadfastly adopt a “categories with families” point of view in describing a morphism
(3)in \begin{equation} E \longrightarrow U \end{equation}
\begin{equation} E \longrightarrow U \end{equation}
 $\widehat{{\mathbb{C}}}$
equivalently as an object in(4)that is, as a presheaf on the category of elements
$\widehat{{\mathbb{C}}}$
equivalently as an object in(4)that is, as a presheaf on the category of elements \begin{equation} \widehat{{\mathbb{C}}}/_U\ \simeq \ \widehat{\textstyle\int _{{\mathbb{C}}}U}\,, \end{equation}
\begin{equation} \widehat{{\mathbb{C}}}/_U\ \simeq \ \widehat{\textstyle\int _{{\mathbb{C}}}U}\,, \end{equation}
 $\int _{{\mathbb{C}}}U$
, where:Thus, the argument
$\int _{{\mathbb{C}}}U$
, where:Thus, the argument \begin{equation*} E(I)\ =\ { \coprod\nolimits_{A\in U(I)}{\mathcal {E}l}(I, A)}\,. \end{equation*}
\begin{equation*} E(I)\ =\ { \coprod\nolimits_{A\in U(I)}{\mathcal {E}l}(I, A)}\,. \end{equation*}
 $(I, A) \in \int _{{\mathbb{C}}}U$
in (2) consists of an object
$(I, A) \in \int _{{\mathbb{C}}}U$
in (2) consists of an object
 $I\in{\mathbb{C}}$
and an element
$I\in{\mathbb{C}}$
and an element
 $A\in U(I)$
.
$A\in U(I)$
.
-
3. In order to account for size issues, the authors assume a Grothendieck universe
 $\textsf{U}$
in
$\textsf{U}$
in
 $\textsf{Set}$
, the elements of which are called small. The category
$\textsf{Set}$
, the elements of which are called small. The category
 $\mathbb{C}$
is then assumed to be small, as are the values of the presheaves, unless otherwise stated.
$\mathbb{C}$
is then assumed to be small, as are the values of the presheaves, unless otherwise stated.
The presheaf
![]() $U$
, which is not small, is regarded as the Grothendieck universe
$U$
, which is not small, is regarded as the Grothendieck universe
![]() $\textsf{U}$
“lifted” from
$\textsf{U}$
“lifted” from
![]() $\textsf{Set}$
to
$\textsf{Set}$
to
![]() $[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]$
. We will analyze the construction of
$[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]$
. We will analyze the construction of
![]() $(U,{\mathcal{E}l})$
from a slightly different perspective in order to arrive at its basic property as a classifier for small families in
$(U,{\mathcal{E}l})$
from a slightly different perspective in order to arrive at its basic property as a classifier for small families in
![]() $\widehat{\mathbb{C}}$
.
$\widehat{\mathbb{C}}$
.
2. An Unused Adjunction
For any presheaf
![]() $X$
on
$X$
on
![]() $\mathbb{C}$
, recall that the category of elements is the comma category,
$\mathbb{C}$
, recall that the category of elements is the comma category,
where
![]() ${\textsf{y}}_{\mathbb{C}} :{\mathbb{C}} \rightarrow{[{{\mathbb{C}}^{\textrm{op}}},\textsf{Set}]}$
is the Yoneda embedding, which we may suppress and write simply
${\textsf{y}}_{\mathbb{C}} :{\mathbb{C}} \rightarrow{[{{\mathbb{C}}^{\textrm{op}}},\textsf{Set}]}$
is the Yoneda embedding, which we may suppress and write simply
![]() ${\mathbb{C}}/_X$
. While the category of elements
${\mathbb{C}}/_X$
. While the category of elements
![]() $\int _{\mathbb{C}} X$
is used in the specification of the Hofmann–Streicher universe
$\int _{\mathbb{C}} X$
is used in the specification of the Hofmann–Streicher universe
![]() $(U,{\mathcal{E}l})$
at the point (4), the authors seem to have missed a trick which simplifies things:Footnote 1
$(U,{\mathcal{E}l})$
at the point (4), the authors seem to have missed a trick which simplifies things:Footnote 1
Proposition 1 (Awodey, Reference Awodey2023, §28). The category of elements functor
![]() $\int _{\mathbb{C}} : \widehat{\mathbb{C}} \longrightarrow{\textsf{Cat}}$
has a right adjoint, which we denote
$\int _{\mathbb{C}} : \widehat{\mathbb{C}} \longrightarrow{\textsf{Cat}}$
has a right adjoint, which we denote
For a small category
![]() $\mathbb{A}$
, we call the presheaf
$\mathbb{A}$
, we call the presheaf
![]() $\nu _{\mathbb{C}}({\mathbb{A}})$
the
$\nu _{\mathbb{C}}({\mathbb{A}})$
the
![]() $\mathbb{C}$
-nerve of
$\mathbb{C}$
-nerve of
![]() $\mathbb{A}$
.
$\mathbb{A}$
.
Proof.
As suggested by the name, the adjunction
![]() $\int _{\mathbb{C}}\! \dashv \nu _{\mathbb{C}}$
can be seen as the familiar “realization
$\int _{\mathbb{C}}\! \dashv \nu _{\mathbb{C}}$
can be seen as the familiar “realization
![]() $\dashv$
nerve” construction with respect to the covariant post-composition functor
$\dashv$
nerve” construction with respect to the covariant post-composition functor
![]() ${\mathbb{C}}/- :{\mathbb{C}}\rightarrow{\textsf{Cat}}$
, as indicated below.
${\mathbb{C}}/- :{\mathbb{C}}\rightarrow{\textsf{Cat}}$
, as indicated below.

In detail, for
![]() ${\mathbb{A}}\in{\textsf{Cat}}$
and
${\mathbb{A}}\in{\textsf{Cat}}$
and
![]() $c\in{\mathbb{C}}$
, let
$c\in{\mathbb{C}}$
, let
![]() $\nu _{{\mathbb{C}}}({\mathbb{A}})(c)$
be the Hom-set of functors,
$\nu _{{\mathbb{C}}}({\mathbb{A}})(c)$
be the Hom-set of functors,
with contravariant action on
![]() $h : d\rightarrow c$
given by pre-composing a functor
$h : d\rightarrow c$
given by pre-composing a functor
![]() $P :{{\mathbb{C}}/_c}\rightarrow{\mathbb{A}}$
with the post-composition functor
$P :{{\mathbb{C}}/_c}\rightarrow{\mathbb{A}}$
with the post-composition functor
For the adjunction, observe that the slice category
![]() ${\mathbb{C}}/_c$
is the category of elements of the representable functor
${\mathbb{C}}/_c$
is the category of elements of the representable functor
![]() ${\textsf{y}}{c}$
,
${\textsf{y}}{c}$
,
Thus for representables
![]() ${\textsf{y}}{c}$
, we indeed have the required natural isomorphism
${\textsf{y}}{c}$
, we indeed have the required natural isomorphism
For arbitrary presheaves
![]() $X$
, one uses the presentation of
$X$
, one uses the presentation of
![]() $X$
as a colimit of representables over the index category
$X$
as a colimit of representables over the index category
![]() $\int _{\mathbb{C}} X$
, and the easy-to-prove fact that
$\int _{\mathbb{C}} X$
, and the easy-to-prove fact that
![]() $\int _{\mathbb{C}}$
itself preserves colimits. Indeed, for any category
$\int _{\mathbb{C}}$
itself preserves colimits. Indeed, for any category
![]() $\mathbb{D}$
, we have an isomorphism in
$\mathbb{D}$
, we have an isomorphism in
![]() $\textsf{Cat}$
,
$\textsf{Cat}$
,
When
![]() $\mathbb{C}$
is fixed, as here, we may omit the subscript from the expressions
$\mathbb{C}$
is fixed, as here, we may omit the subscript from the expressions
![]() ${\textsf{y}}_{\mathbb{C}}$
and
${\textsf{y}}_{\mathbb{C}}$
and
![]() $\int _{\mathbb{C}}$
and
$\int _{\mathbb{C}}$
and
![]() $\nu _{\mathbb{C}}$
. The unit and counit maps of the adjunction
$\nu _{\mathbb{C}}$
. The unit and counit maps of the adjunction
![]() $\int \dashv \nu$
,
$\int \dashv \nu$
,
are as follows. At
![]() $c\in{\mathbb{C}}$
, for
$c\in{\mathbb{C}}$
, for
![]() $x :{\textsf{y}}{c}{\rightarrow } X$
, the functor
$x :{\textsf{y}}{c}{\rightarrow } X$
, the functor
![]() $(\eta _X)_c(x) :{\mathbb{C}}/_c \rightarrow{\mathbb{C}}/_X$
is just composition with
$(\eta _X)_c(x) :{\mathbb{C}}/_c \rightarrow{\mathbb{C}}/_X$
is just composition with
![]() $x$
,
$x$
,
For
![]() ${\mathbb{A}}\in{\textsf{Cat}}$
, the functor
${\mathbb{A}}\in{\textsf{Cat}}$
, the functor
![]() $ \epsilon : \int \nu{\mathbb{A}} \rightarrow{\mathbb{A}}$
takes a pair
$ \epsilon : \int \nu{\mathbb{A}} \rightarrow{\mathbb{A}}$
takes a pair
![]() $(c\in{\mathbb{C}}, f :{\mathbb{C}}/_c \rightarrow{\mathbb{A}})$
to the object
$(c\in{\mathbb{C}}, f :{\mathbb{C}}/_c \rightarrow{\mathbb{A}})$
to the object
![]() $f(1_c) \in{\mathbb{A}}$
,
$f(1_c) \in{\mathbb{A}}$
,
Lemma 2.
For any
![]() $f : Y\rightarrow X$
, the naturality square below is a pullback.
$f : Y\rightarrow X$
, the naturality square below is a pullback.

Proof.
It suffices to prove this for the case
![]() $f : X{\rightarrow } 1$
. Thus, consider the square
$f : X{\rightarrow } 1$
. Thus, consider the square

Evaluating at
![]() $c\in{\mathbb{C}}$
and applying (6) then gives the following square in
$c\in{\mathbb{C}}$
and applying (6) then gives the following square in
![]() $\textsf{Set}$
.
$\textsf{Set}$
.

The image of
![]() $*\in 1c$
along the bottom is the forgetful functor
$*\in 1c$
along the bottom is the forgetful functor
![]() $U_c :{\mathbb{C}}/_c\rightarrow{\mathbb{C}}$
, and its fiber under the map on the right is therefore the set of functors
$U_c :{\mathbb{C}}/_c\rightarrow{\mathbb{C}}$
, and its fiber under the map on the right is therefore the set of functors
![]() $F :{{\mathbb{C}}/_c}\rightarrow{{\mathbb{C}}/_X}$
such that
$F :{{\mathbb{C}}/_c}\rightarrow{{\mathbb{C}}/_X}$
such that
![]() $U_X\circ F = U_c$
, where
$U_X\circ F = U_c$
, where
![]() $U_X :{\mathbb{C}}/_X\rightarrow{\mathbb{C}}$
is also a forgetful functor. But any such
$U_X :{\mathbb{C}}/_X\rightarrow{\mathbb{C}}$
is also a forgetful functor. But any such
![]() $F$
is easily seen to be uniquely of the form
$F$
is easily seen to be uniquely of the form
![]() ${\mathbb{C}}/_{x}$
for
${\mathbb{C}}/_{x}$
for
![]() $x = F(1_c) :{\textsf{y}}{c} \rightarrow X$
.
$x = F(1_c) :{\textsf{y}}{c} \rightarrow X$
.
Remark 3.
The category of elements of the terminal presheaf
![]() $1$
is
$1$
is
![]() $\mathbb{C}$
itself,
$\mathbb{C}$
itself,
![]() $\int \!{1} \cong{\mathbb{C}}$
. So for every presheaf
$\int \!{1} \cong{\mathbb{C}}$
. So for every presheaf
![]() $X$
, there is a canonical projection
$X$
, there is a canonical projection
![]() $\int \!{X} \rightarrow{\mathbb{C}}$
, and the functor
$\int \!{X} \rightarrow{\mathbb{C}}$
, and the functor
![]() $\int : \widehat{\mathbb{C}} \rightarrow{\textsf{Cat}}$
thus factors through the slice category
$\int : \widehat{\mathbb{C}} \rightarrow{\textsf{Cat}}$
thus factors through the slice category
![]() ${\textsf{Cat}}/_{\mathbb{C}}$
.
${\textsf{Cat}}/_{\mathbb{C}}$
.

The adjunction
![]() $\int \dashv \nu :{\textsf{Cat}} \rightarrow \widehat{\mathbb{C}}$
factors as well, but it is the unfactored adjunction that is more useful for the present purpose.
$\int \dashv \nu :{\textsf{Cat}} \rightarrow \widehat{\mathbb{C}}$
factors as well, but it is the unfactored adjunction that is more useful for the present purpose.
3. Classifying Families
For every presheaf
![]() $X$
, the canonical projection
$X$
, the canonical projection
![]() $\int \!{X}{\rightarrow }{\mathbb{C}}$
of Remark 3 is easily seen to be a discrete fibration. It follows that for any natural transformation
$\int \!{X}{\rightarrow }{\mathbb{C}}$
of Remark 3 is easily seen to be a discrete fibration. It follows that for any natural transformation
![]() $Y\rightarrow X$
, the associated functor
$Y\rightarrow X$
, the associated functor
![]() $\int \!{Y} \rightarrow \int \!{X}$
is also a discrete fibration. Ignoring size issues for the moment, recall that discrete fibrations in
$\int \!{Y} \rightarrow \int \!{X}$
is also a discrete fibration. Ignoring size issues for the moment, recall that discrete fibrations in
![]() $\textsf{Cat}$
are classified by the forgetful functor
$\textsf{Cat}$
are classified by the forgetful functor
![]() ${{\dot{{\textsf{Set}}}}^{\textrm{op}}}\rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
from (the opposites of) the category of pointed sets to that of sets (cf. Weber, Reference Weber2007). For every presheaf
${{\dot{{\textsf{Set}}}}^{\textrm{op}}}\rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
from (the opposites of) the category of pointed sets to that of sets (cf. Weber, Reference Weber2007). For every presheaf
![]() $X\in \widehat{{\mathbb{C}}}$
, we therefore have a pullback diagram in
$X\in \widehat{{\mathbb{C}}}$
, we therefore have a pullback diagram in
![]() $\textsf{Cat}$
,
$\textsf{Cat}$
,

Using
![]() $\int \!{1} \cong{\mathbb{C}}$
and transposing by the adjunction
$\int \!{1} \cong{\mathbb{C}}$
and transposing by the adjunction
![]() $\int \dashv \nu$
then gives a commutative square in
$\int \dashv \nu$
then gives a commutative square in
![]() $\widehat{{\mathbb{C}}}$
,
$\widehat{{\mathbb{C}}}$
,

Lemma 4.
The square (12) is a pullback in
![]() $\widehat{{\mathbb{C}}}$
. More generally, for any map
$\widehat{{\mathbb{C}}}$
. More generally, for any map
![]() $Y{\rightarrow } X$
in
$Y{\rightarrow } X$
in
![]() $\widehat{{\mathbb{C}}}$
, there is a pullback square
$\widehat{{\mathbb{C}}}$
, there is a pullback square

Proof.
Apply the right adjoint
![]() $\nu$
to the pullback square (11) and paste the naturality square (7) from Lemma 2 on the left, to obtain the transposed square (13) as a pasting of two pullbacks.
$\nu$
to the pullback square (11) and paste the naturality square (7) from Lemma 2 on the left, to obtain the transposed square (13) as a pasting of two pullbacks.
Let us write
![]() ${\dot{\mathcal{V}}} \rightarrow{\mathcal{V}}$
for the vertical map on the right in (13); that is, let
${\dot{\mathcal{V}}} \rightarrow{\mathcal{V}}$
for the vertical map on the right in (13); that is, let
We can then summarize our results so far as follows.
Proposition 5.
The nerve
![]() ${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
of the classifier for discrete fibrations
${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
of the classifier for discrete fibrations
![]() ${{{\,\dot{{\textsf{Set}}}}}^{\textrm{op}}}\rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
, as defined in (14), classifies natural transformations
${{{\,\dot{{\textsf{Set}}}}}^{\textrm{op}}}\rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
, as defined in (14), classifies natural transformations
![]() $Y\rightarrow X$
in
$Y\rightarrow X$
in
![]() $\widehat{{\mathbb{C}}}$
, in the sense that there is always a pullback square,
$\widehat{{\mathbb{C}}}$
, in the sense that there is always a pullback square,

The classifying map
![]() $\tilde{Y} : X\rightarrow{\mathcal{V}}$
is determined by the adjunction
$\tilde{Y} : X\rightarrow{\mathcal{V}}$
is determined by the adjunction
![]() $\int \dashv \nu$
as the transpose of the classifying map of the discrete fibration
$\int \dashv \nu$
as the transpose of the classifying map of the discrete fibration
![]() $\int \!{Y}\rightarrow \int \!{X}$
.
$\int \!{Y}\rightarrow \int \!{X}$
.
The classifying map
![]() $\tilde{Y} : X\rightarrow{\mathcal{V}}$
of a given natural transformation
$\tilde{Y} : X\rightarrow{\mathcal{V}}$
of a given natural transformation
![]() $Y\rightarrow X$
is, of course, not in general unique. Nonetheless, we can make use of the construction of
$Y\rightarrow X$
is, of course, not in general unique. Nonetheless, we can make use of the construction of
![]() ${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
as the nerve of the discrete fibration classifier
${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
as the nerve of the discrete fibration classifier
![]() ${{{\,\dot{{\textsf{Set}}}}}^{\textrm{op}}}\rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
, for which classifying functors
${{{\,\dot{{\textsf{Set}}}}}^{\textrm{op}}}\rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
, for which classifying functors
![]() ${\mathbb{C}} \rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
are unique up to natural isomorphism, to infer the following proposition, which plays a role in Shulman (Reference Shulman2015),Gratzer et al. (Reference Gratzer, Shulman and Sterling2024) and elsewhere.
${\mathbb{C}} \rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
are unique up to natural isomorphism, to infer the following proposition, which plays a role in Shulman (Reference Shulman2015),Gratzer et al. (Reference Gratzer, Shulman and Sterling2024) and elsewhere.
Proposition 6 (Realignment). Given a monomorphism
![]() $c : C{\rightarrowtail } X$
and a family
$c : C{\rightarrowtail } X$
and a family
![]() $Y\rightarrow X$
, let
$Y\rightarrow X$
, let
![]() $y_c : C \rightarrow{\mathcal{V}}$
classify the pullback
$y_c : C \rightarrow{\mathcal{V}}$
classify the pullback
![]() $c^*Y\rightarrow C$
. Then there is a classifying map
$c^*Y\rightarrow C$
. Then there is a classifying map
![]() $y: X \rightarrow{\mathcal{V}}$
for
$y: X \rightarrow{\mathcal{V}}$
for
![]() $Y\rightarrow X$
with
$Y\rightarrow X$
with
![]() $y\circ c = y_c$
.
$y\circ c = y_c$
.

Proof.
Transposing the realignment problem (16) for presheaves across the adjunction
![]() $\int \dashv \nu$
results in the following realignment problem for discrete fibrations.
$\int \dashv \nu$
results in the following realignment problem for discrete fibrations.

The category of elements functor
![]() $\int$
is easily seen to preserve pullbacks, hence monos; thus let us consider the general case of a functor
$\int$
is easily seen to preserve pullbacks, hence monos; thus let us consider the general case of a functor
![]() $C :{\mathbb{C}}{\rightarrowtail }{\mathbb{D}}$
which is monic in
$C :{\mathbb{C}}{\rightarrowtail }{\mathbb{D}}$
which is monic in
![]() $\textsf{Cat}$
, a pullback of discrete fibrations as on the left below, and a presheaf
$\textsf{Cat}$
, a pullback of discrete fibrations as on the left below, and a presheaf
![]() $E :{\mathbb{C}} \rightarrow{{{{\textsf{Set}}}}^{\textrm{op}}}$
with
$E :{\mathbb{C}} \rightarrow{{{{\textsf{Set}}}}^{\textrm{op}}}$
with
![]() $\int \!{E} \cong \mathbb{E}$
over
$\int \!{E} \cong \mathbb{E}$
over
![]() $\mathbb{C}$
.
$\mathbb{C}$
.

We seek
![]() $F :{\mathbb{D}} \rightarrow{{{{\textsf{Set}}}}^{\textrm{op}}}$
with
$F :{\mathbb{D}} \rightarrow{{{{\textsf{Set}}}}^{\textrm{op}}}$
with
![]() $\int \!{F} \cong \mathbb{F}$
over
$\int \!{F} \cong \mathbb{F}$
over
![]() $\mathbb{D}$
and
$\mathbb{D}$
and
![]() $F\circ C = E$
. Let
$F\circ C = E$
. Let
![]() $F_0 :{\mathbb{D}} \rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
with
$F_0 :{\mathbb{D}} \rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
with
![]() $\int \!{F}_0 \cong \mathbb{F}$
over
$\int \!{F}_0 \cong \mathbb{F}$
over
![]() $\mathbb{D}$
. Since
$\mathbb{D}$
. Since
![]() $F_0\circ C$
and
$F_0\circ C$
and
![]() $E$
both classify
$E$
both classify
![]() $\mathbb{E}$
, there is a natural iso
$\mathbb{E}$
, there is a natural iso
![]() $e : F_0\circ C \cong E$
. Consider the following diagram
$e : F_0\circ C \cong E$
. Consider the following diagram

where
![]() ${\textsf{Set}}^{\cong }$
is the category of isos in
${\textsf{Set}}^{\cong }$
is the category of isos in
![]() $\textsf{Set}$
, with
$\textsf{Set}$
, with
![]() $p_1, p_2$
the (opposites of the) domain and codomain projections. There is a well-known weak factorization system on
$p_1, p_2$
the (opposites of the) domain and codomain projections. There is a well-known weak factorization system on
![]() $\textsf{Cat}$
(part of the “canonical model structure”) with injective-on-objects functors on the left and isofibration equivalences on the right. Thus, there is a diagonal filler
$\textsf{Cat}$
(part of the “canonical model structure”) with injective-on-objects functors on the left and isofibration equivalences on the right. Thus, there is a diagonal filler
![]() $f$
as indicated. The functor
$f$
as indicated. The functor
![]() $F := p_2 f :{\mathbb{D}} \rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
is then the one we seek.
$F := p_2 f :{\mathbb{D}} \rightarrow{{{\textsf{Set}}}^{\textrm{op}}}$
is then the one we seek.
Of course, as defined in (14), the classifier
![]() ${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
cannot be a map in
${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
cannot be a map in
![]() $\widehat{{\mathbb{C}}}$
, for reasons of size; we now address this.
$\widehat{{\mathbb{C}}}$
, for reasons of size; we now address this.
4. Small Maps
For any cardinal number
![]() $\alpha$
, call a set
$\alpha$
, call a set
![]() $\alpha$
-small if its cardinality is strictly less than
$\alpha$
-small if its cardinality is strictly less than
![]() $\alpha$
. Let
$\alpha$
. Let
![]() ${\textsf{Set}}_\alpha{\hookrightarrow }{\textsf{Set}}$
be the full subcategory of
${\textsf{Set}}_\alpha{\hookrightarrow }{\textsf{Set}}$
be the full subcategory of
![]() $\alpha$
-small sets. Call a map
$\alpha$
-small sets. Call a map
![]() $f:Y\rightarrow X$
of presheaves
$f:Y\rightarrow X$
of presheaves
![]() $\alpha$
-small if all of the fibers
$\alpha$
-small if all of the fibers
![]() $f_c^{-1}\{ x\} \subseteq Yc$
are
$f_c^{-1}\{ x\} \subseteq Yc$
are
![]() $\alpha$
-small sets (for all
$\alpha$
-small sets (for all
![]() $c\in{\mathbb{C}}$
and
$c\in{\mathbb{C}}$
and
![]() $x\in Xc$
). The latter condition is equivalent to saying that for any element
$x\in Xc$
). The latter condition is equivalent to saying that for any element
![]() $x:{\textsf{y}}{c} \rightarrow X$
, the set of lifts
$x:{\textsf{y}}{c} \rightarrow X$
, the set of lifts
![]() $y:{\textsf{y}}{c} \rightarrow Y$
of
$y:{\textsf{y}}{c} \rightarrow Y$
of
![]() $x$
across
$x$
across
![]() $f$
is
$f$
is
![]() $\alpha$
-small.
$\alpha$
-small.

Finally, call a presheaf
![]() $X :{{{\mathbb{C}}}^{\textrm{op}}} \rightarrow{\textsf{Set}}$
$X :{{{\mathbb{C}}}^{\textrm{op}}} \rightarrow{\textsf{Set}}$
![]() $\alpha$
-small if the map
$\alpha$
-small if the map
![]() $X\rightarrow 1$
is
$X\rightarrow 1$
is
![]() $\alpha$
-small. This implies that all of the values
$\alpha$
-small. This implies that all of the values
![]() $Xc$
are
$Xc$
are
![]() $\alpha$
-small sets, and so the functor
$\alpha$
-small sets, and so the functor
![]() $X :{{{\mathbb{C}}}^{\textrm{op}}} \rightarrow{\textsf{Set}}$
factors through
$X :{{{\mathbb{C}}}^{\textrm{op}}} \rightarrow{\textsf{Set}}$
factors through
![]() ${\textsf{Set}}_\alpha{\hookrightarrow }{\textsf{Set}}$
.
${\textsf{Set}}_\alpha{\hookrightarrow }{\textsf{Set}}$
.
Now let us restrict the specification (14) of
![]() ${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
to the
${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
to the
![]() $\alpha$
-small sets:
$\alpha$
-small sets:
Then, the evident forgetful map
![]() ${\dot{\mathcal{V}}}_\alpha \rightarrow{\mathcal{V}}_\alpha$
is a map in the category
${\dot{\mathcal{V}}}_\alpha \rightarrow{\mathcal{V}}_\alpha$
is a map in the category
![]() $\widehat{{\mathbb{C}}}$
of presheaves, and it is in fact
$\widehat{{\mathbb{C}}}$
of presheaves, and it is in fact
![]() $\alpha$
-small, as the reader can easily check. Moreover, it has the following basic property, which is just a restriction of the basic property of
$\alpha$
-small, as the reader can easily check. Moreover, it has the following basic property, which is just a restriction of the basic property of
![]() ${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
stated in Proposition 5.
${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
stated in Proposition 5.
Proposition 7.
The map
![]() ${\dot{\mathcal{V}}}_\alpha \rightarrow{\mathcal{V}}_\alpha$
classifies
${\dot{\mathcal{V}}}_\alpha \rightarrow{\mathcal{V}}_\alpha$
classifies
![]() $\alpha$
-small maps
$\alpha$
-small maps
![]() $f:Y\rightarrow X$
in
$f:Y\rightarrow X$
in
![]() $\widehat{{\mathbb{C}}}$
, in the sense that there is always a pullback square,
$\widehat{{\mathbb{C}}}$
, in the sense that there is always a pullback square,

The classifying map
![]() $\tilde{Y} : X\rightarrow{\mathcal{V}}_\alpha$
is determined by the adjunction
$\tilde{Y} : X\rightarrow{\mathcal{V}}_\alpha$
is determined by the adjunction
![]() $\int \dashv \nu$
as (the factorization of) the transpose of the classifying map of the discrete fibration
$\int \dashv \nu$
as (the factorization of) the transpose of the classifying map of the discrete fibration
![]() $\int \!{X}\rightarrow \int \!{Y}$
.
$\int \!{X}\rightarrow \int \!{Y}$
.
Proof.
If
![]() $Y\rightarrow X$
is
$Y\rightarrow X$
is
![]() $\alpha$
-small, its classifying map
$\alpha$
-small, its classifying map
![]() $\tilde{Y} : X\rightarrow{\mathcal{V}}$
factors through
$\tilde{Y} : X\rightarrow{\mathcal{V}}$
factors through
![]() ${\mathcal{V}}_\alpha{\hookrightarrow }{\mathcal{V}}$
, as indicated below,
${\mathcal{V}}_\alpha{\hookrightarrow }{\mathcal{V}}$
, as indicated below,

in virtue of the following adjoint transposition,

Note that the square on the right is evidently a pullback, and so the one on the left is one, too, because the outer rectangle is the classifying pullback of the discrete fibration
![]() $\int \!{Y} \rightarrow \int \!{X}$
, as stated. Thus, the left square in (23) is a pullback.
$\int \!{Y} \rightarrow \int \!{X}$
, as stated. Thus, the left square in (23) is a pullback.
5. Examples
-
1. Let
 $\alpha = \kappa$
a strongly inaccessible cardinal, so that
$\alpha = \kappa$
a strongly inaccessible cardinal, so that
 $\textsf{ob}({{\textsf{Set}}_\kappa })$
is a Grothendieck universe. Then, the Hofmann–Streicher universe of (3) is recovered in the present setting as the
$\textsf{ob}({{\textsf{Set}}_\kappa })$
is a Grothendieck universe. Then, the Hofmann–Streicher universe of (3) is recovered in the present setting as the
 $\kappa$
-small map classifierin the sense of Proposition 7. Indeed, for
$\kappa$
-small map classifierin the sense of Proposition 7. Indeed, for \begin{equation*} E\, \cong \, {\dot {\mathcal {V}}}_\kappa \longrightarrow {\mathcal {V}}_\kappa \, \cong \, U \end{equation*}
\begin{equation*} E\, \cong \, {\dot {\mathcal {V}}}_\kappa \longrightarrow {\mathcal {V}}_\kappa \, \cong \, U \end{equation*}
 $c\in{\mathbb{C}}$
, we have(25)For
$c\in{\mathbb{C}}$
, we have(25)For \begin{align}{\mathcal{V}}_{\kappa }{c}\ &=\ \nu ({\textsf{Set}}^{\textsf{op}}_\kappa )(c) ={\textsf{Cat}}\big ({{\mathbb{C}}/_c}\,,\,{\textsf{Set}}^{\textsf{op}}_\kappa \big )\ =\ \textsf{ob}(\widehat{{\mathbb{C}}/_c})\ =\ U{c} \,. \end{align}
\begin{align}{\mathcal{V}}_{\kappa }{c}\ &=\ \nu ({\textsf{Set}}^{\textsf{op}}_\kappa )(c) ={\textsf{Cat}}\big ({{\mathbb{C}}/_c}\,,\,{\textsf{Set}}^{\textsf{op}}_\kappa \big )\ =\ \textsf{ob}(\widehat{{\mathbb{C}}/_c})\ =\ U{c} \,. \end{align}
 ${\dot{\mathcal{V}}}_{\kappa }$
we then have,(26)where the
${\dot{\mathcal{V}}}_{\kappa }$
we then have,(26)where the \begin{align} {\dot{\mathcal{V}}}_{\kappa }{c}\ =\ \nu ({\,\dot{{\textsf{Set}}}}^{\textsf{op}}_\kappa )(c)\ &=\ {\textsf{Cat}}\big ({{\mathbb{C}}/_c}\,,\,{\,\dot{{\textsf{Set}}}}^{\textsf{op}}_\kappa \big ) \notag \\ &\cong \ { \coprod _{A\in{\mathcal{V}}_{\kappa }{c}}{\textsf{Cat}}_{{{\mathbb{C}}/_c}}\big ({{\mathbb{C}}/_c}\,,\, A^*{\textsf{Set}}^{\textsf{op}}_\kappa \big )} \end{align}
\begin{align} {\dot{\mathcal{V}}}_{\kappa }{c}\ =\ \nu ({\,\dot{{\textsf{Set}}}}^{\textsf{op}}_\kappa )(c)\ &=\ {\textsf{Cat}}\big ({{\mathbb{C}}/_c}\,,\,{\,\dot{{\textsf{Set}}}}^{\textsf{op}}_\kappa \big ) \notag \\ &\cong \ { \coprod _{A\in{\mathcal{V}}_{\kappa }{c}}{\textsf{Cat}}_{{{\mathbb{C}}/_c}}\big ({{\mathbb{C}}/_c}\,,\, A^*{\textsf{Set}}^{\textsf{op}}_\kappa \big )} \end{align}
 $A$
-summand in (26) is defined by taking sections of the pullback indicated below.
(27)
$A$
-summand in (26) is defined by taking sections of the pullback indicated below.
(27)
But
 $A^*{\textsf{Set}}^{\textsf{op}}_\kappa \ \cong \ { \int _{{\mathbb{C}}/_c}\!A}$
over
$A^*{\textsf{Set}}^{\textsf{op}}_\kappa \ \cong \ { \int _{{\mathbb{C}}/_c}\!A}$
over
 ${\mathbb{C}}/_c\,$
, and sections of this discrete fibration in
${\mathbb{C}}/_c\,$
, and sections of this discrete fibration in
 $\textsf{Cat}$
correspond uniquely to natural maps
$\textsf{Cat}$
correspond uniquely to natural maps
 $1\rightarrow A$
in
$1\rightarrow A$
in
 $\widehat{{{\mathbb{C}}/_c}}$
. Since
$\widehat{{{\mathbb{C}}/_c}}$
. Since
 $1$
is representable in
$1$
is representable in
 $\widehat{{{\mathbb{C}}/_c}}$
, we can continue (26) by
$\widehat{{{\mathbb{C}}/_c}}$
, we can continue (26) by \begin{align*}{\dot{\mathcal{V}}}_{\kappa }{c}\ &\cong \ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}}{\textsf{Cat}}_{{{\mathbb{C}}/_c}}\big ({{\mathbb{C}}/_c}\,,\, A^*{\textsf{Set}}^{\textsf{op}}_\kappa \big )}\\ &\cong \ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}} \widehat{{{\mathbb{C}}/_c}}(1, A)}\\ &\cong \ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}} A(1_c) } \\ & =\ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}}{\mathcal{E}l}(\langle c, A\rangle )}\\ & =\ E c\,. \end{align*}
\begin{align*}{\dot{\mathcal{V}}}_{\kappa }{c}\ &\cong \ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}}{\textsf{Cat}}_{{{\mathbb{C}}/_c}}\big ({{\mathbb{C}}/_c}\,,\, A^*{\textsf{Set}}^{\textsf{op}}_\kappa \big )}\\ &\cong \ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}} \widehat{{{\mathbb{C}}/_c}}(1, A)}\\ &\cong \ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}} A(1_c) } \\ & =\ { \coprod\nolimits_{A\in{\mathcal{V}}_{\kappa }{c}}{\mathcal{E}l}(\langle c, A\rangle )}\\ & =\ E c\,. \end{align*}
-
2. By functoriality of the nerve
 $\nu :{\textsf{Cat}} \rightarrow \widehat{{\mathbb{C}}}$
, a sequence of Grothendieck universesin
$\nu :{\textsf{Cat}} \rightarrow \widehat{{\mathbb{C}}}$
, a sequence of Grothendieck universesin \begin{equation*}{\textsf {U}}_0 \subseteq {\textsf {U}}_1 \subseteq \ldots \end{equation*}
\begin{equation*}{\textsf {U}}_0 \subseteq {\textsf {U}}_1 \subseteq \ldots \end{equation*}
 $\textsf{Set}$
gives rise to a (cumulative) sequence of type-theoretic universesin
$\textsf{Set}$
gives rise to a (cumulative) sequence of type-theoretic universesin \begin{equation*}{\mathcal {V}}_0 {\rightarrowtail } {\mathcal {V}}_1 {\rightarrowtail } \ldots \end{equation*}
\begin{equation*}{\mathcal {V}}_0 {\rightarrowtail } {\mathcal {V}}_1 {\rightarrowtail } \ldots \end{equation*}
 $\widehat{{\mathbb{C}}}$
. More precisely, there is a sequence of Cartesian squares,
(28)
$\widehat{{\mathbb{C}}}$
. More precisely, there is a sequence of Cartesian squares,
(28)
in the image of
 $\nu :{\textsf{Cat}}\longrightarrow \widehat{\mathbb{C}}$
, classifying small maps in
$\nu :{\textsf{Cat}}\longrightarrow \widehat{\mathbb{C}}$
, classifying small maps in
 $\widehat{\mathbb{C}}$
of increasing size, in the sense of Proposition 7.
$\widehat{\mathbb{C}}$
of increasing size, in the sense of Proposition 7. -
3. Let
 $\alpha = 2$
so that
$\alpha = 2$
so that
 $1\rightarrow 2$
is the subobject classifier of
$1\rightarrow 2$
is the subobject classifier of
 $\textsf{Set}$
, and
$\textsf{Set}$
, and
is then a classifier in
 $\textsf{Cat}$
for sieves, i.e. full subcategories
$\textsf{Cat}$
for sieves, i.e. full subcategories
 $\mathbb{S}{\hookrightarrow }{\mathbb{A}}$
closed under the domains of arrows
$\mathbb{S}{\hookrightarrow }{\mathbb{A}}$
closed under the domains of arrows
 $a\rightarrow s$
for
$a\rightarrow s$
for
 $s\in \mathbb{S}$
(equivalently, discrete fibrations whose fibers are truth-values). The nerve
$s\in \mathbb{S}$
(equivalently, discrete fibrations whose fibers are truth-values). The nerve
 ${\dot{\mathcal{V}}}_{2} \rightarrow{\mathcal{V}}_{2}$
is then the usual subobject classifier
${\dot{\mathcal{V}}}_{2} \rightarrow{\mathcal{V}}_{2}$
is then the usual subobject classifier
 $1\rightarrow \Omega$
of the presheaf topos
$1\rightarrow \Omega$
of the presheaf topos
 $\widehat{\mathbb{C}}$
,
$\widehat{\mathbb{C}}$
,
-
4. Let
 be the embedding-retraction pair with
be the embedding-retraction pair with  the inclusion of the full subcategory on the sets
the inclusion of the full subcategory on the sets
 $ \{0, 1\}$
and
$ \{0, 1\}$
and  the retraction that takes
the retraction that takes
 $0 = \emptyset$
to itself, and everything else (i.e. the non-empty sets) to
$0 = \emptyset$
to itself, and everything else (i.e. the non-empty sets) to
 $1 = \{\emptyset \}$
. There is a retraction (of arrows) in
$1 = \{\emptyset \}$
. There is a retraction (of arrows) in
 $\textsf{Cat}$
,(29)
$\textsf{Cat}$
,(29)
where the left square is a pullback.
By the functoriality of (
 ${-}^{\textrm{op}}$
and)
${-}^{\textrm{op}}$
and)
 $\nu :{\textsf{Cat}} \rightarrow \widehat{{\mathbb{C}}}$
, we then have a retract diagram in
$\nu :{\textsf{Cat}} \rightarrow \widehat{{\mathbb{C}}}$
, we then have a retract diagram in
 $\widehat{\mathbb{C}}$
, again with a pullback on the left,(30)
$\widehat{\mathbb{C}}$
, again with a pullback on the left,(30)
where for any
 $\phi : X\rightarrow \Omega$
the subobject
$\phi : X\rightarrow \Omega$
the subobject
 $\{\phi \}{\rightarrowtail } X$
is classified as a small map by the composite
$\{\phi \}{\rightarrowtail } X$
is classified as a small map by the composite
 $\{\phi \} : X\rightarrow{\mathcal{V}}_\kappa$
, and for any small map
$\{\phi \} : X\rightarrow{\mathcal{V}}_\kappa$
, and for any small map
 $A\rightarrow X$
, the image
$A\rightarrow X$
, the image
 $[A]{\rightarrowtail } X$
is classified as a subobject by the composite
$[A]{\rightarrowtail } X$
is classified as a subobject by the composite
 $[\alpha ] : X\rightarrow{\mathcal{V}}_\kappa \rightarrow \Omega$
, where
$[\alpha ] : X\rightarrow{\mathcal{V}}_\kappa \rightarrow \Omega$
, where
 $\alpha : X\rightarrow{\mathcal{V}}_\kappa$
classifies
$\alpha : X\rightarrow{\mathcal{V}}_\kappa$
classifies
 $A\rightarrow X$
. The idempotent compositeis the propositional truncation modality in the natural model of type theory given by
$A\rightarrow X$
. The idempotent compositeis the propositional truncation modality in the natural model of type theory given by \begin{equation*}|\!|\!-\!|\!| = \{[-]\} : {\mathcal {V}}_\kappa \longrightarrow {\mathcal {V}}_\kappa \end{equation*}
\begin{equation*}|\!|\!-\!|\!| = \{[-]\} : {\mathcal {V}}_\kappa \longrightarrow {\mathcal {V}}_\kappa \end{equation*}
 ${\dot{\mathcal{V}}}_\kappa \rightarrow{\mathcal{V}}_\kappa$
(see Awodey et al., Reference Awodey, Gambino and Hazratpour2024).
${\dot{\mathcal{V}}}_\kappa \rightarrow{\mathcal{V}}_\kappa$
(see Awodey et al., Reference Awodey, Gambino and Hazratpour2024).
6. Change of Base
Let
![]() $F :{\mathbb{C}} \rightarrow{\mathbb{D}}$
in
$F :{\mathbb{C}} \rightarrow{\mathbb{D}}$
in
![]() $\textsf{Cat}$
and consider the base change:
$\textsf{Cat}$
and consider the base change:

How is the universal (small) map
![]() ${\dot{\mathcal{V}}}_{\mathbb{C}}\rightarrow{\mathcal{V}}_{\mathbb{C}}$
in
${\dot{\mathcal{V}}}_{\mathbb{C}}\rightarrow{\mathcal{V}}_{\mathbb{C}}$
in
![]() $[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]$
related to
$[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]$
related to
![]() ${\dot{\mathcal{V}}}_{\mathbb{D}}\rightarrow{\mathcal{V}}_{\mathbb{D}}$
in
${\dot{\mathcal{V}}}_{\mathbb{D}}\rightarrow{\mathcal{V}}_{\mathbb{D}}$
in
![]() $[{{{\mathbb{D}}}^{\textrm{op}}},\textsf{Set}]$
?
$[{{{\mathbb{D}}}^{\textrm{op}}},\textsf{Set}]$
?
For each
![]() $c\in{\mathbb{C}}$
, we have the sliced functor
$c\in{\mathbb{C}}$
, we have the sliced functor
![]() $F/_{c} :{\mathbb{C}}/_c \rightarrow{\mathbb{D}}/_{Fc}$
which is the component at
$F/_{c} :{\mathbb{C}}/_c \rightarrow{\mathbb{D}}/_{Fc}$
which is the component at
![]() $c\in{\mathbb{C}}$
of a natural transformation
$c\in{\mathbb{C}}$
of a natural transformation
![]() $F/ :{\mathbb{C}}/ \rightarrow{\mathbb{D}}/\circ F$
as functors
$F/ :{\mathbb{C}}/ \rightarrow{\mathbb{D}}/\circ F$
as functors
![]() ${\mathbb{C}} \rightarrow{\textsf{Cat}}$
.
${\mathbb{C}} \rightarrow{\textsf{Cat}}$
.

Indeed, for each
![]() $h : c \rightarrow c'$
there is a commutative square:
$h : c \rightarrow c'$
there is a commutative square:

The 2-cell
![]() $F/ :{\mathbb{C}}/ \rightarrow{\mathbb{D}}/\circ F$
in (32) (left Kan) extends to one,
$F/ :{\mathbb{C}}/ \rightarrow{\mathbb{D}}/\circ F$
in (32) (left Kan) extends to one,

which has the following 2-categorical mate.

Evaluating at the (small) discrete fibration classifier
![]() ${{{\,\dot{{\textsf{set}}}}}^{\textrm{op}}}\rightarrow{{{\textsf{set}}}^{\textrm{op}}}$
, we obtain a commutative square in
${{{\,\dot{{\textsf{set}}}}}^{\textrm{op}}}\rightarrow{{{\textsf{set}}}^{\textrm{op}}}$
, we obtain a commutative square in
![]() $\widehat{\mathbb{C}}$
of the form
$\widehat{\mathbb{C}}$
of the form

where we have written
for the components of
![]() $\nu _F$
.
$\nu _F$
.
Proposition 8 (Base change for universes). For any functor
![]() $F:{\mathbb{C}}\rightarrow{\mathbb{D}}$
, the comparison square (36) for universes is a pullback in
$F:{\mathbb{C}}\rightarrow{\mathbb{D}}$
, the comparison square (36) for universes is a pullback in
![]() $\widehat{\mathbb{C}} ={[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]}$
.
$\widehat{\mathbb{C}} ={[{{{\mathbb{C}}}^{\textrm{op}}},\textsf{Set}]}$
.
For the proof, we require the following.
Lemma 9.
For any functor
![]() $F:{\mathbb{C}}\rightarrow{\mathbb{D}}$
and any
$F:{\mathbb{C}}\rightarrow{\mathbb{D}}$
and any
![]() $c\in{\mathbb{C}}$
, the sliced functor
$c\in{\mathbb{C}}$
, the sliced functor
![]() $F/_c:{\mathbb{C}}/_c \longrightarrow{\mathbb{D}}/_{Fc}$
is final.
$F/_c:{\mathbb{C}}/_c \longrightarrow{\mathbb{D}}/_{Fc}$
is final.
Proof.
Recall that a functor
![]() $F:{\mathbb{C}}\rightarrow{\mathbb{D}}$
is by definition final if for all
$F:{\mathbb{C}}\rightarrow{\mathbb{D}}$
is by definition final if for all
![]() $G:{\mathbb{D}}\rightarrow{\textsf{Set}}$
, the canonical map
$G:{\mathbb{D}}\rightarrow{\textsf{Set}}$
, the canonical map
![]() $\varinjlim G\circ F \rightarrow \varinjlim G$
is an iso, and this holds just if, for all
$\varinjlim G\circ F \rightarrow \varinjlim G$
is an iso, and this holds just if, for all
![]() $d\in{\mathbb{D}}$
, the comma category
$d\in{\mathbb{D}}$
, the comma category
![]() $d/_F$
is connected. Moreover, recall from Street and Walters (Reference Street and Walters1973) that the comprehensive factorization system
$d/_F$
is connected. Moreover, recall from Street and Walters (Reference Street and Walters1973) that the comprehensive factorization system
![]() $(\textsf{Fin}, \textsf{dFib})$
on
$(\textsf{Fin}, \textsf{dFib})$
on
![]() $\textsf{Cat}$
has the final functors as left orthogonal to the discrete fibrations. But now note that the slice categories
$\textsf{Cat}$
has the final functors as left orthogonal to the discrete fibrations. But now note that the slice categories
![]() ${\mathbb{C}}/_c$
and
${\mathbb{C}}/_c$
and
![]() ${\mathbb{D}}/_{Fc}$
have terminal objects, preserved by
${\mathbb{D}}/_{Fc}$
have terminal objects, preserved by
![]() $F/_c:{\mathbb{C}}/_c \longrightarrow{\mathbb{D}}/_{Fc}$
. It therefore suffices to observe that the inclusion functor
$F/_c:{\mathbb{C}}/_c \longrightarrow{\mathbb{D}}/_{Fc}$
. It therefore suffices to observe that the inclusion functor
![]() $i : \{1_{\mathbb{C}}\}{\hookrightarrow }{\mathbb{C}}$
of a terminal object is always final, so the same is true for
$i : \{1_{\mathbb{C}}\}{\hookrightarrow }{\mathbb{C}}$
of a terminal object is always final, so the same is true for
![]() $F/_c:{\mathbb{C}}/_c \longrightarrow{\mathbb{D}}/_{Fc}$
by a familiar factorization property of the left maps in an orthogonal factorization system.
$F/_c:{\mathbb{C}}/_c \longrightarrow{\mathbb{D}}/_{Fc}$
by a familiar factorization property of the left maps in an orthogonal factorization system.
Proof.
(of Proposition 8) Evaluating (36) at
![]() $c\in{\mathbb{C}}$
, we obtain the following diagram of sets and functions.
$c\in{\mathbb{C}}$
, we obtain the following diagram of sets and functions.

The outer square of this diagram is a pullback exactly if every square as follows has a diagonal filler.

Since the map on the right is the universal small discrete fibration, this condition obtains just in case the map on the left is left orthogonal with respect to all small discrete fibrations (for “small” sufficiently large), which holds just if it is a final functor, by the comprehensive factorization system Street and Walters (Reference Street and Walters1973). But by Lemma 9, this is the case for every
![]() $c\in{\mathbb{C}}$
.
$c\in{\mathbb{C}}$
.
7. Classifying Fibrations
Given the universal small family
![]() ${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
of Proposition 7, we first construct a classifier
${\dot{\mathcal{V}}}\rightarrow{\mathcal{V}}$
of Proposition 7, we first construct a classifier
![]() ${\,\dot{\mathcal{U}}}\rightarrow{\mathcal{U}}$
for any structured notion of fibration using the method of classifying types developed in Awodey et al. (Reference Awodey, Gambino and Hazratpour2024) (which in turn is based on Shulman’s locally representable notion of fibered structure (Shulman, Reference Shulman2019)). We consider the behavior of such universal maps under base change in the next section.
${\,\dot{\mathcal{U}}}\rightarrow{\mathcal{U}}$
for any structured notion of fibration using the method of classifying types developed in Awodey et al. (Reference Awodey, Gambino and Hazratpour2024) (which in turn is based on Shulman’s locally representable notion of fibered structure (Shulman, Reference Shulman2019)). We consider the behavior of such universal maps under base change in the next section.
Suppose that for each object
![]() $X$
and family
$X$
and family
![]() $A\rightarrow X$
, there is a family
$A\rightarrow X$
, there is a family
![]() ${\textsf{Fib}}(A){\rightarrow } X$
that classifies fibration structures on
${\textsf{Fib}}(A){\rightarrow } X$
that classifies fibration structures on
![]() $A\rightarrow X$
, in the sense that there is a bijection, natural in
$A\rightarrow X$
, in the sense that there is a bijection, natural in
![]() $X$
, between sections of
$X$
, between sections of
![]() ${\textsf{Fib}}(A){\rightarrow } X$
and (a notion of) fibration structures on
${\textsf{Fib}}(A){\rightarrow } X$
and (a notion of) fibration structures on
![]() $A\rightarrow X$
. Naturality in
$A\rightarrow X$
. Naturality in
![]() $X$
means that
$X$
means that
![]() ${\textsf{Fib}}(A){\rightarrow } X$
is stable under pullback, in the sense that for any
${\textsf{Fib}}(A){\rightarrow } X$
is stable under pullback, in the sense that for any
![]() $f:Y{\rightarrow } X$
, we have two pullback squares:
$f:Y{\rightarrow } X$
, we have two pullback squares:

Thus,
It then follows from Proposition 7 that, if
![]() $A{\rightarrow } X$
is small, then
$A{\rightarrow } X$
is small, then
![]() ${\textsf{Fib}}(A){\rightarrow } X$
is itself a pullback of the analogous object
${\textsf{Fib}}(A){\rightarrow } X$
is itself a pullback of the analogous object
![]() ${\textsf{Fib}}({\dot{\mathcal{V}}}){\rightarrow }{\mathcal{V}}$
constructed from the universal small family
${\textsf{Fib}}({\dot{\mathcal{V}}}){\rightarrow }{\mathcal{V}}$
constructed from the universal small family
![]() ${\dot{\mathcal{V}}}{\rightarrow }{\mathcal{V}}$
. So again there are two pullback squares,
${\dot{\mathcal{V}}}{\rightarrow }{\mathcal{V}}$
. So again there are two pullback squares,

where the indicated map
![]() $X \rightarrow{\mathcal{V}}$
is the canonical classifier of
$X \rightarrow{\mathcal{V}}$
is the canonical classifier of
![]() $A\rightarrow X$
.
$A\rightarrow X$
.
Proposition 10. There is a universal small fibration,
Every small fibration
![]() $A{\rightarrow } X$
is a pullback of
$A{\rightarrow } X$
is a pullback of
![]() ${\,\dot{\mathcal{U}}}{\rightarrow }{\mathcal{U}}$
along a canonical classifying map
${\,\dot{\mathcal{U}}}{\rightarrow }{\mathcal{U}}$
along a canonical classifying map
![]() $X{\rightarrow }{\mathcal{U}}$
.
$X{\rightarrow }{\mathcal{U}}$
.

Proof. We can take
which comes with its canonical projection
![]() ${\textsf{Fib}}({\dot{\mathcal{V}}}){\rightarrow }{\mathcal{V}}$
as in diagram (40). Now define
${\textsf{Fib}}({\dot{\mathcal{V}}}){\rightarrow }{\mathcal{V}}$
as in diagram (40). Now define
![]() ${\,\dot{\mathcal{U}}}{\rightarrow }{\mathcal{U}}$
by pulling back the universal small family,
${\,\dot{\mathcal{U}}}{\rightarrow }{\mathcal{U}}$
by pulling back the universal small family,

Consider the following diagram, in which all the squares (including the distorted ones) are pullbacks, with the outer vertical one coming from Proposition 7 and the lower horizontal one from (40).

By assumption, a fibration structure
![]() $\alpha$
on
$\alpha$
on
![]() $A{\rightarrow } X$
is a section of
$A{\rightarrow } X$
is a section of
![]() ${\textsf{Fib}}(A)\rightarrow X$
, which is the pullback of
${\textsf{Fib}}(A)\rightarrow X$
, which is the pullback of
![]() ${\textsf{Fib}}({\dot{\mathcal{V}}})={\mathcal{U}}$
along the classifying map
${\textsf{Fib}}({\dot{\mathcal{V}}})={\mathcal{U}}$
along the classifying map
![]() $a: X \rightarrow{\mathcal{V}}$
,
$a: X \rightarrow{\mathcal{V}}$
,
Such sections therefore correspond uniquely to factorizations
![]() $\alpha '$
of
$\alpha '$
of
![]() $a : X\rightarrow{\mathcal{V}}$
, as indicated, which in turn induce pullback squares of the required kind (41).
$a : X\rightarrow{\mathcal{V}}$
, as indicated, which in turn induce pullback squares of the required kind (41).
Finally, observe that the map
![]() ${\,\dot{\mathcal{U}}}\rightarrow{\mathcal{U}}$
has a canonical fibration structure. Indeed, consider the following diagram, in which both squares are pullbacks.
${\,\dot{\mathcal{U}}}\rightarrow{\mathcal{U}}$
has a canonical fibration structure. Indeed, consider the following diagram, in which both squares are pullbacks.

Since
![]() ${\textsf{Fib}}({\dot{\mathcal{V}}})$
is the object of fibration structures on
${\textsf{Fib}}({\dot{\mathcal{V}}})$
is the object of fibration structures on
![]() ${\dot{\mathcal{V}}}{\rightarrow }{\mathcal{V}}$
, its pullback
${\dot{\mathcal{V}}}{\rightarrow }{\mathcal{V}}$
, its pullback
![]() ${\textsf{Fib}}({\,\dot{\mathcal{U}}})$
is the object of fibration structures on
${\textsf{Fib}}({\,\dot{\mathcal{U}}})$
is the object of fibration structures on
![]() ${\,\dot{\mathcal{U}}}{\rightarrow }{\mathcal{U}}$
. But since
${\,\dot{\mathcal{U}}}{\rightarrow }{\mathcal{U}}$
. But since
![]() ${\mathcal{U}} ={\textsf{Fib}}({\dot{\mathcal{V}}})$
by definition, the lower square is the pullback of
${\mathcal{U}} ={\textsf{Fib}}({\dot{\mathcal{V}}})$
by definition, the lower square is the pullback of
![]() ${\textsf{Fib}}({\dot{\mathcal{V}}}){\rightarrow }{\mathcal{V}}$
against itself, which does indeed have a distinguished section, namely the diagonal
${\textsf{Fib}}({\dot{\mathcal{V}}}){\rightarrow }{\mathcal{V}}$
against itself, which does indeed have a distinguished section, namely the diagonal
8. Change of Base for Universal Fibrations
Now let
![]() $F :{\mathbb{C}} \rightarrow{\mathbb{D}}$
in
$F :{\mathbb{C}} \rightarrow{\mathbb{D}}$
in
![]() $\textsf{Cat}$
with
$\textsf{Cat}$
with
![]() ${\dot{\mathcal{V}}}_{\mathbb{C}}\rightarrow{\mathcal{V}}_{\mathbb{C}}$
in
${\dot{\mathcal{V}}}_{\mathbb{C}}\rightarrow{\mathcal{V}}_{\mathbb{C}}$
in
![]() $\widehat{{\mathbb{C}}}$
and
$\widehat{{\mathbb{C}}}$
and
![]() ${\dot{\mathcal{V}}}_{\mathbb{D}}\rightarrow{\mathcal{V}}_{\mathbb{D}}$
in
${\dot{\mathcal{V}}}_{\mathbb{D}}\rightarrow{\mathcal{V}}_{\mathbb{D}}$
in
![]() $\widehat{{\mathbb{D}}}$
, related by the base change geometric morphism
$\widehat{{\mathbb{D}}}$
, related by the base change geometric morphism
as in Proposition 8, and suppose that we have a structured notion of fibration in
![]() $\widehat{\mathbb{C}}$
, classified by
$\widehat{\mathbb{C}}$
, classified by
![]() ${\,\dot{\mathcal{U}}}_{\mathbb{C}} \rightarrow{\mathcal{U}}_{\mathbb{C}}$
as in Proposition 10. Then, we can transfer a structured notion of fibration to
${\,\dot{\mathcal{U}}}_{\mathbb{C}} \rightarrow{\mathcal{U}}_{\mathbb{C}}$
as in Proposition 10. Then, we can transfer a structured notion of fibration to
![]() $\widehat{{\mathbb{D}}}$
by declaring
$\widehat{{\mathbb{D}}}$
by declaring
![]() $B\rightarrow Y$
to be a fibration in
$B\rightarrow Y$
to be a fibration in
![]() $\widehat{{\mathbb{D}}}$
just if
$\widehat{{\mathbb{D}}}$
just if
![]() $F^*B\rightarrow F^*Y$
is one in
$F^*B\rightarrow F^*Y$
is one in
![]() $\widehat{\mathbb{C}}$
; more precisely, we define a fibration structure on
$\widehat{\mathbb{C}}$
; more precisely, we define a fibration structure on
![]() $B\rightarrow Y$
to be one on
$B\rightarrow Y$
to be one on
![]() $F^*B\rightarrow F^*Y$
. These structures are then classified in
$F^*B\rightarrow F^*Y$
. These structures are then classified in
![]() $\widehat{{\mathbb{D}}}$
, as follows.
$\widehat{{\mathbb{D}}}$
, as follows.
Fibration structures on
![]() $F^*B\rightarrow F^*Y$
are classified in
$F^*B\rightarrow F^*Y$
are classified in
![]() $\widehat{{\mathbb{C}}}$
by sections
$\widehat{{\mathbb{C}}}$
by sections
![]() $\sigma$
of
$\sigma$
of
![]() ${\textsf{Fib}}(F^*B)\rightarrow F^*Y$
,
${\textsf{Fib}}(F^*B)\rightarrow F^*Y$
,

Applying the right adjoint
![]() $F_*$
and pulling back along the unit
$F_*$
and pulling back along the unit
![]() $\eta$
, we obtain an object over
$\eta$
, we obtain an object over
![]() $Y$
that classifies such sections.
$Y$
that classifies such sections.

Indeed, sections of
![]() ${\textsf{Fib}}(B) \rightarrow Y$
correspond bijectively to lifts of the unit
${\textsf{Fib}}(B) \rightarrow Y$
correspond bijectively to lifts of the unit
![]() $\eta$
across the image
$\eta$
across the image
![]() $F_*{\textsf{Fib}}(F^*B) \rightarrow F_*F^*Y$
under
$F_*{\textsf{Fib}}(F^*B) \rightarrow F_*F^*Y$
under
![]() $F_*$
, which are exactly sections of
$F_*$
, which are exactly sections of
![]() ${\textsf{Fib}}(F^*B) \rightarrow F^*Y$
.
${\textsf{Fib}}(F^*B) \rightarrow F^*Y$
.
As before, it suffices to do this construction once in the “universal case,”

to obtain the classifying type for fibrations in
![]() $\widehat{\mathbb{D}}$
as (the domain of) the indicated map
$\widehat{\mathbb{D}}$
as (the domain of) the indicated map
Proposition 11.
Let
![]() ${\,\dot{\mathcal{U}}}_{\mathbb{D}} \rightarrow{\mathcal{U}}_{\mathbb{D}}$
be the pullback indicated below,
${\,\dot{\mathcal{U}}}_{\mathbb{D}} \rightarrow{\mathcal{U}}_{\mathbb{D}}$
be the pullback indicated below,

where
![]() ${\mathcal{U}}_{\mathbb{D}} \rightarrow{\mathcal{V}}_{\mathbb{D}}$
is as defined in (48). Then,
${\mathcal{U}}_{\mathbb{D}} \rightarrow{\mathcal{V}}_{\mathbb{D}}$
is as defined in (48). Then,
![]() ${\,\dot{\mathcal{U}}}_{\mathbb{D}} \rightarrow{\mathcal{U}}_{\mathbb{D}}$
classifies fibrations in
${\,\dot{\mathcal{U}}}_{\mathbb{D}} \rightarrow{\mathcal{U}}_{\mathbb{D}}$
classifies fibrations in
![]() $\widehat{\mathbb{D}}$
.
$\widehat{\mathbb{D}}$
.
Proof.
Proposition 10 applies once we know that
![]() ${\textsf{Fib}}(-)$
as defined in (45) is stable under pullback. It clearly suffices to show that, for each
${\textsf{Fib}}(-)$
as defined in (45) is stable under pullback. It clearly suffices to show that, for each
![]() $B\rightarrow Y$
, the horizontal square below is a pullback when
$B\rightarrow Y$
, the horizontal square below is a pullback when
![]() $b : Y\rightarrow{\mathcal{V}}_{\mathbb{D}}$
is the canonical classifying map.
$b : Y\rightarrow{\mathcal{V}}_{\mathbb{D}}$
is the canonical classifying map.

Inspecting the definitions (45) and (48), this follows from the naturality of the units
![]() $\eta$
,
$\eta$
,

Indeed, consider the following cube, in which the front face is the naturality square (50) and the top and bottom faces are the defining pullbacks (46) and (47) of
![]() ${\textsf{Fib}}(B)$
and
${\textsf{Fib}}(B)$
and
![]() ${\mathcal{U}}_{\mathbb{D}} ={\textsf{Fib}}({\dot{\mathcal{V}}}_{\mathbb{D}})$
respectively.
${\mathcal{U}}_{\mathbb{D}} ={\textsf{Fib}}({\dot{\mathcal{V}}}_{\mathbb{D}})$
respectively.

It suffices to show that the right face is a pullback, and since
![]() $F_*$
preserves pullbacks, it therefore suffices to show that the horizontal square below is a pullback.
$F_*$
preserves pullbacks, it therefore suffices to show that the horizontal square below is a pullback.

But that follows from the stability of
![]() $\textsf{Fib}$
in
$\textsf{Fib}$
in
![]() $\widehat{\mathbb{C}}$
and preservation by
$\widehat{\mathbb{C}}$
and preservation by
![]() $F^*$
of the classifying pullback square for
$F^*$
of the classifying pullback square for
![]() $B\rightarrow Y$
.
$B\rightarrow Y$
.
Thus, as claimed, we have:
Theorem 12 (Base change for universes of fibrations). Let
![]() $F :{\mathbb{C}} \rightarrow{\mathbb{D}}$
with base change
$F :{\mathbb{C}} \rightarrow{\mathbb{D}}$
with base change
and suppose that we have a structured notion of fibration in
![]() $\widehat{\mathbb{C}}$
classified by a universe
$\widehat{\mathbb{C}}$
classified by a universe
![]() ${\,\dot{\mathcal{U}}}_{\mathbb{C}} \rightarrow{\mathcal{U}}_{\mathbb{C}}$
. Then, the structured notion of fibration in
${\,\dot{\mathcal{U}}}_{\mathbb{C}} \rightarrow{\mathcal{U}}_{\mathbb{C}}$
. Then, the structured notion of fibration in
![]() $\widehat{{\mathbb{D}}}$
determined by pullback along
$\widehat{{\mathbb{D}}}$
determined by pullback along
![]() $F^*$
is classified by
$F^*$
is classified by
![]() ${\,\dot{\mathcal{U}}}_{{\mathbb{D}}} \rightarrow{\mathcal{U}}_{{\mathbb{D}}}$
where
${\,\dot{\mathcal{U}}}_{{\mathbb{D}}} \rightarrow{\mathcal{U}}_{{\mathbb{D}}}$
where
Theorem 12 is used in Awodey et al. (Reference Awodey, Cavallo, Coquand, Riehl and Sattler2014) to move the universe of fibrations in a model of type theory from the interval model in cubical species
![]() ${\textsf{cSet}}^\Sigma = [{{\Box }^{\textrm{op}}}\times \Sigma,{\textsf{Set}}]$
to the equivariant one in cubical sets
${\textsf{cSet}}^\Sigma = [{{\Box }^{\textrm{op}}}\times \Sigma,{\textsf{Set}}]$
to the equivariant one in cubical sets
![]() ${\textsf{cSet}} = [{{\Box }^{\textrm{op}}},{\textsf{Set}}]$
along the base change induced by the projection functor
${\textsf{cSet}} = [{{\Box }^{\textrm{op}}},{\textsf{Set}}]$
along the base change induced by the projection functor
![]() ${{\Box }^{\textrm{op}}}\times \Sigma \rightarrow{{\Box }^{\textrm{op}}}$
.
${{\Box }^{\textrm{op}}}\times \Sigma \rightarrow{{\Box }^{\textrm{op}}}$
.
Acknowledgements
Thanks to Mathieu Anel, Reid Barton, Thierry Coquand, Marcelo Fiore, and Emily Riehl for discussions, and to Evan Cavallo, Ivan Di Liberti, and Taichi Uemura for help with the references. This material is based upon work supported by the Air Force Office of Scientific Research under awards FA9550-21-1-0009 and FA9550-20-1-0305.