Published online by Cambridge University Press: 18 January 2013
We study monadic translations of the call-by-name (cbn) and call-by-value (cbv) fragments of the classical sequent calculus 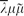 ${\overline{\lambda}\mu\tilde{\mu}}$ due to Curien and Herbelin, and give modular and syntactic proofs of strong normalisation. The target of the translations is a new meta-language for classical logic, named monadic λμ. This language is a monadic reworking of Parigot's λμ-calculus, where the monadic binding is confined to commands, thus integrating the monad with the classical features. Also, its μ-reduction rule is replaced by a rule expressing the interaction between monadic binding and μ-abstraction.
${\overline{\lambda}\mu\tilde{\mu}}$ due to Curien and Herbelin, and give modular and syntactic proofs of strong normalisation. The target of the translations is a new meta-language for classical logic, named monadic λμ. This language is a monadic reworking of Parigot's λμ-calculus, where the monadic binding is confined to commands, thus integrating the monad with the classical features. Also, its μ-reduction rule is replaced by a rule expressing the interaction between monadic binding and μ-abstraction.
Our monadic translations produce very tight simulations of the respective fragments of 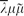 ${\overline{\lambda}\mu\tilde{\mu}}$ within monadic λμ, with reduction steps of
${\overline{\lambda}\mu\tilde{\mu}}$ within monadic λμ, with reduction steps of 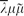 ${\overline{\lambda}\mu\tilde{\mu}}$ being translated in a 1–1 fashion, except for β steps, which require two steps. The monad of monadic λμ can be instantiated to the continuations monad so as to ensure strict simulation of monadic λμ within simply typed λ-calculus with β- and η-reduction. Through strict simulation, the strong normalisation of simply typed λ-calculus is inherited by monadic λμ, and then by cbn and cbv
${\overline{\lambda}\mu\tilde{\mu}}$ being translated in a 1–1 fashion, except for β steps, which require two steps. The monad of monadic λμ can be instantiated to the continuations monad so as to ensure strict simulation of monadic λμ within simply typed λ-calculus with β- and η-reduction. Through strict simulation, the strong normalisation of simply typed λ-calculus is inherited by monadic λμ, and then by cbn and cbv 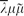 ${\overline{\lambda}\mu\tilde{\mu}}$, thus reproving strong normalisation in an elementary syntactical way for these fragments of
${\overline{\lambda}\mu\tilde{\mu}}$, thus reproving strong normalisation in an elementary syntactical way for these fragments of 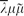 ${\overline{\lambda}\mu\tilde{\mu}}$, and establishing it for our new calculus. These results extend to second-order logic, with polymorphic λ-calculus as the target, giving new strong normalisation results for classical second-order logic in sequent calculus style.
${\overline{\lambda}\mu\tilde{\mu}}$, and establishing it for our new calculus. These results extend to second-order logic, with polymorphic λ-calculus as the target, giving new strong normalisation results for classical second-order logic in sequent calculus style.
CPS translations of cbn and cbv 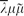 ${\overline{\lambda}\mu\tilde{\mu}}$ with the strict simulation property are obtained by composing our monadic translations with the continuations-monad instantiation. In an appendix to the paper, we investigate several refinements of the continuations-monad instantiation in order to obtain in a modular way improvements of the CPS translations enjoying extra properties like simulation by cbv β-reduction or reduction of administrative redexes at compile time.
${\overline{\lambda}\mu\tilde{\mu}}$ with the strict simulation property are obtained by composing our monadic translations with the continuations-monad instantiation. In an appendix to the paper, we investigate several refinements of the continuations-monad instantiation in order to obtain in a modular way improvements of the CPS translations enjoying extra properties like simulation by cbv β-reduction or reduction of administrative redexes at compile time.