Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-09T03:26:03.635Z Has data issue: false hasContentIssue false
  • English
  • Français

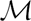$\mathcal{M}$-adhesive transformation systems with nested application conditions. Part 1: parallelism, concurrency and amalgamation

Published online by Cambridge University Press:  26 June 2014

HARTMUT EHRIG ,
ULRIKE GOLAS ,
ANNEGRET HABEL ,
LEEN LAMBERS  and
FERNANDO OREJAS
HARTMUT EHRIG
Affiliation:
Technische Universität Berlin, Berlin, Germany Email: [email protected]
ULRIKE GOLAS
Affiliation:
Konrad-Zuse-Zentrum für Informationstechnik Berlin, Berlin, Germany Email: [email protected]
ANNEGRET HABEL
Affiliation:
Universität Oldenburg, Oldenburg, Germany Email: [email protected]
LEEN LAMBERS
Affiliation:
Hasso-Plattner-Institut, Universität Potsdam, Potsdam, Germany Email: [email protected]
FERNANDO OREJAS
Affiliation:
Universitat Politècnica de Catalunya, Barcelona, Spain Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

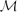Nested application conditions generalise the well-known negative application conditions and are important for several application domains. In this paper, we present Local Church–Rosser, Parallelism, Concurrency and Amalgamation Theorems for rules with nested application conditions in the framework of $\mathcal{M}$-adhesive categories, where 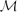$\mathcal{M}$-adhesive categories are slightly more general than weak adhesive high-level replacement categories. Most of the proofs are based on the corresponding statements for rules without application conditions and two shift lemmas stating that nested application conditions can be shifted over morphisms and rules.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 24 , Issue 4: Structure Transformation , August 2014 , 240406
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adámek, J., Herrlich, H. and Strecker, G. (1990) Abstract and Concrete Categories, John Wiley.Google Scholar
Arbib, M. A. and Manes, E. G. (1975) Arrows, Structures, and Functors, Academic Press.Google Scholar
Baader, F. and Nipkow, T. (1998) Term Rewriting and All That, Cambridge University Press.Google Scholar
Baldan, P., Gadducci, F. and Sobocinski, P. (2011) Adhesivity is not enough: Local Church–Rosser revisited. In: Mathematical Foundations of Computer Science (MFCS 2011). Springer-Verlag Lecture Notes in Computer Science 6907 48–59.CrossRefGoogle Scholar
Biermann, E., Ehrig, H., Ermel, C., Golas, U. and Taentzer, G. (2010) Parallel independence of amalgamated graph transformations applied to model transformation. In: Graph Transformations and Model-Driven Engineering. Springer-Verlag Lecture Notes in Computer Science 5765 121–140.CrossRefGoogle Scholar
Boehm, P., Fonio, H.-R. and Habel, A. (1987) Amalgamation of graph transformations: A synchronization mechanism. Journal of Computer and System Sciences 34 377–408.Google Scholar
Bruggink, H. J. S., Cauderlier, R., Hülsbusch, M. and König, B. (2011) Conditional reactive systems. In: Foundations of Software Technology and Theoretical Computer Science (FSTTCS 2011) 191–203.Google Scholar
Castellani, I. and Montanari, U. (1983) Graph grammars for distributed systems. In: Graph Grammars and Their Application to Computer Science. Springer-Verlag Lecture Notes in Computer Science 153 20–38.CrossRefGoogle Scholar
Corradini, A., Montanari, U., Rossi, F., Ehrig, H., Heckel, R. and Löwe, M. (1997) Algebraic approaches to graph transformation. Part I: Basic concepts and double pushout approach. In: Handbook of Graph Grammars and Computing by Graph Transformation 1, World Scientific 163–245.Google Scholar
Corradini, A., Rossi, F. and Parisi-Presicce, F. (1991) Logic programming as hypergraph rewriting. In: Proceedings of the International Joint Conference on Theory and Practice of Software Development (TAPSOFT'91). Springer-Verlag Lecture Notes in Computer Science 493 275–295.CrossRefGoogle Scholar
Courcelle, B. (1997) The expression of graph properties and graph transformations in monadic second-order logic. In: Handbook of Graph Grammars and Computing by Graph Transformation 1, World Scientific 313–400.Google Scholar
Csuhaj-Varjú, E. (1993) On grammars with local and global context conditions. International Journal of Computer Mathematics 47 17–27.Google Scholar
Dassow, J. and Păun, G. (1989) Regulated Rewriting in Formal Language Theory, EATCS Monographs on Theoretical Computer Science 18, Springer-Verlag.CrossRefGoogle Scholar
Degano, P. and Montanari, U. (1987) A model of distributed systems based on graph rewriting. Journal of the ACM 34 411–449.CrossRefGoogle Scholar
Dijkstra, E. W. (1965) Solution of a Problem in Concurrent Programming Control. Communications of the ACM 8 569.Google Scholar
Dijkstra, E. W. (1976) A Discipline of Programming, Prentice-Hall.Google Scholar
Ehrig, H. (1979) Introduction to the algebraic theory of graph grammars. In: Graph-Grammars and Their Application to Computer Science and Biology. Springer-Verlag Lecture Notes in Computer Science 73 1–69.Google Scholar
Ehrig, H. and Habel, A. (1986) Graph grammars with application conditions. In: Rozenberg, G. and Salomaa, A. (eds.) The Book of L, Springer-Verlag 87–100.Google Scholar
Ehrig, H. and Kreowski, H.-J. (1980) Applications of graph grammar theory to consistency, synchronization and scheduling in database systems. Information Systems 5 225–238.Google Scholar
Ehrig, H. and Parisi-Presicce, F. (1992) High-level-replacement systems for equational algebraic specifications. In: Algebraic and Logic Programming – proceedings Third International Conference. Springer-Verlag Lecture Notes in Computer Science 632 3–20.Google Scholar
Ehrig, H. and Rosen, B. (1980) Parallelism and concurrency of graph manipulations. Theoretical Computer Science 11 247–275.Google Scholar
Ehrig, H., Ehrig, K., Habel, A. and Pennemann, K.-H. (2006) Theory of constraints and application conditions: From graphs to high-level structures. Fundamenta Informaticae 74 (1)135–166.Google Scholar
Ehrig, H., Ehrig, K., Prange, U. and Taentzer, G. (2006) Fundamentals of Algebraic Graph Transformation. EATCS Monographs of Theoretical Computer Science, Springer-Verlag.Google Scholar
Ehrig, H., Engels, G., Kreowski, H.-J. and Rozenberg, G. (eds.) (1999) Handbook of Graph Grammars and Computing by Graph Transformation 2: Applications, Languages and Tools, World Scientific.Google Scholar
Ehrig, H., Golas, U. and Hermann, F. (2010) Categorical Frameworks for Graph Transformation and HLR Systems based on the DPO Approach. Bulletin of the EATCS 112 111–121.Google Scholar
Ehrig, H., Golas, U., Habel, A., Lambers, L. and Orejas, F. (2012) $\mathcal{M}$-Adhesive Transformation Systems with Nested Application Conditions. Part 2: Embedding, Critical Pairs and Local Confluence. Fundamenta Informaticae 118 35–63Google Scholar
Ehrig, H., Habel, A. and Lambers, L. (2010) Parallelism and concurrency theorems for rules with nested application conditions. Electronic Communications of the EASST 26.Google Scholar
Ehrig, H., Habel, A. and Rosen, B. K. (1986) Concurrent transformations of relational structures. Fundamenta Informaticae IX 13–50.CrossRefGoogle Scholar
Ehrig, H., Habel, A., Kreowski, H.-J. and Parisi-Presicce, F. (1991) Parallelism and concurrency in high level replacement systems. Mathematical Structures in Computer Science 1 361–404.Google Scholar
Ehrig, H., Habel, A., Padberg, J. and Prange, U. (2006) Adhesive high-level replacement systems: A new categorical framework for graph transformation. Fundamenta Informaticae 74 1–29.Google Scholar
Ehrig, H., Hermann, F. and Sartorius, C. (2009) Completeness and Correctness of Model Transformations based on Triple Graph Grammars with Negative Application Conditions. Electronic Communications of the EASST 18.Google Scholar
Ehrig, H., Kreowski, H.-J., Montanari, U. and Rozenberg, G. (eds.) (1999) Handbook of Graph Grammars and Computing by Graph Transformation 3: Concurrency, Parallelism, and Distribution, World Scientific.Google Scholar
Ehrig, K., Küster, J. M. and Taentzer, G. (2009) Generating instance models from meta models. Software and System Modeling 8 (4)479–500.Google Scholar
Ehrig, H., Pfender, M. and Schneider, H.-J. (1973) Graph grammars: An algebraic approach. In: Proceedings of the 14th Annual IEEE Symposium on Switching and Automata Theory 167–180.CrossRefGoogle Scholar
Golas, U. (2011) Analysis and correctness of algebraic graph and model transformation, Vieweg+ Teubner Research.Google Scholar
Golas, U., Habel, A. and Ehrig, H. (2014) Multi-Amalgamation in $\mathcal{M}$-Adhesive Categories. Mathematical Structures in Computer Science (this volume).Google Scholar
Habel, A. and Pennemann, K.-H. (2009) Correctness of high-level transformation systems relative to nested conditions. Mathematical Structures in Computer Science 19 245–296.Google Scholar
Habel, A. and Plump, D. (2001) Computational completeness of programming languages based on graph transformation. In: Foundations of Software Science and Computation Structures – proceedings FOSSACS 2001. Springer-Verlag Lecture Notes in Computer Science 2030 230–245.CrossRefGoogle Scholar
Habel, A. and Radke, H. (2010) Expressiveness of graph conditions with variables. Electronic Communications of the EASST 30.Google Scholar
Habel, A., Heckel, R. and Taentzer, G. (1996) Graph grammars with negative application conditions. Fundamenta Informaticae 26 287–313.Google Scholar
Habel, A., Pennemann, K-H. and Rensink, A. (2006) Weakest preconditions for high-level programs. In: Graph Transformations (ICGT 2006). Springer-Verlag Lecture Notes in Computer Science 4178 445–460.Google Scholar
Heckel, R. and Wagner, A. (1995) Ensuring consistency of conditional graph grammars – a constructive approach. In: Workshop on Graph Rewriting and Computation – proceedings SEGRAGRA'95. Electronic Notes in Theoretical Computer Science 2 95–104.Google Scholar
Heckel, R., Llabrés, M., Ehrig, H. and Orejas, F. (2002) Concurrency and loose semantics of open graph transformation systems. Mathematical Structures in Computer Science 12 (4)349–376.Google Scholar
Heindel, T. (2010) Hereditary Pushouts Reconsidered. In: Graph Transformations (ICGT'10). Springer-Verlag Lecture Notes in Computer Science 6372 250–265.Google Scholar
Hoare, C. A. R. (1969) An axiomatic basis for computer programming. Communications of the ACM 12 576–580, 583.CrossRefGoogle Scholar
Knuth, D. E. and Bendix, P. B. (1970) Simple word problems in universal algebras. In: Computational Problems in Abstract Algebras, Pergamon Press 263–297.Google Scholar
Koch, M., Mancini, L. V. and Parisi-Presicce, F. (2005) Graph-based specification of access control policies. Journal of Computer and System Sciences 71 1–33.Google Scholar
Kreowski, H.-J. (1977) Manipulationen von Graphmanipulationen, Ph.D. thesis, Technical University of Berlin.Google Scholar
Lack, S. and Sobociński, P. (2004) Adhesive categories. In: Foundations of Software Science and Computation Structures (FOSSACS'04). Springer-Verlag Lecture Notes in Computer Science 2987 273–288.Google Scholar
Lack, S. and Sobociński, P. (2005) Adhesive and quasiadhesive categories. Theoretical Informatics and Application 39 (2)511–546.Google Scholar
Lambers, L. (2010) Certifying Rule-Based Models using Graph Transformation, Ph.D. thesis, Technical University of Berlin.Google Scholar
Mahr, B. and Wilharm, A. (1982) Graph grammars as a tool for description in computer processed control: A case study. In: Graph-Theoretic Concepts in Computer Science, Hanser Verlag, München165–176.Google Scholar
Parisi-Presicce, F. (1989) Modular system design applying graph grammar techniques. In: Automata, Languages and Programming – proceedings ICALP89. Springer-Verlag Lecture Notes in Computer Science 372 621–636.Google Scholar
Pennemann, K.-H. (2009) Development of Correct Graph Transformation Systems, Ph.D. thesis, Universität Oldenburg.Google Scholar
Plump, D. (2005) Confluence of graph transformation revisited. In: Processes, Terms and Cycles: Steps on the Road to Infinity – Essays Dedicated to Jan Willem Klop on the Occasion of His 60th Birthday. Springer-Verlag Lecture Notes in Computer Science 3838 280–308.CrossRefGoogle Scholar
Poskitt, C. M. and Plump, D. (2012) Hoare-style verification of graph programs. Fundamenta Informaticae 118 135–175.Google Scholar
Rensink, A. (2004) Representing first-order logic by graphs. In: Graph Transformations – proceedings ICGT'04. Springer-Verlag Lecture Notes in Computer Science 3256 319–335.CrossRefGoogle Scholar
Ribeiro, L. (1996) A telephone's system specification using graph grammars. Technical report 96-23, Technical University of Berlin.Google Scholar
Rosen, B. K. (1975) A Church–Rosser theorem for graph grammars (announcement). SIGACT News 7 (3)26–31.Google Scholar
Rozenberg, G. (ed.) (1997) Handbook of Graph Grammars and Computing by Graph Transformation 1: Foundations, World Scientific.Google Scholar
Salomaa, A. (1973) Formal Languages, Academic Press.Google Scholar
Taentzer, G., Koch, M., Fischer, I. and Volle, V. (1999) Distributed graph transformation with application to visual design of distributed systems. In: Ehrig, H., Kreowski, H.-J., Montanari, U. and Rozenberg, G. (eds.) Handbook of Graph Grammars and Computing by Graph Transformation 3: Concurrency, Parallelism, and Distribution, World Scientific 269–340.Google Scholar
Winkelmann, J., Taentzer, G., Ehrig, K. and Küster, J. M. (2008) Translation of restricted OCL constraints into graph constraints for generating meta model instances by graph grammars. In: Proceedings GT-VMT 2006. Electronic Notes in Theoretical Computer Science 211 159–170.Google Scholar