Article contents
The longest common substring problem
Published online by Cambridge University Press: 29 May 2015
Abstract
Given a set 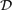 $\mathcal{D}$ of q documents, the Longest Common Substring (LCS) problem asks, for any integer 2 ⩽ k ⩽ q, the longest substring that appears in k documents. LCS is a well-studied problem having a wide range of applications in Bioinformatics: from microarrays to DNA sequences alignments and analysis. This problem has been solved by Hui (2000International Journal of Computer Science and Engineering15 73–76) by using a famous constant-time solution to the Lowest Common Ancestor (LCA) problem in trees coupled with the use of suffix trees.
$\mathcal{D}$ of q documents, the Longest Common Substring (LCS) problem asks, for any integer 2 ⩽ k ⩽ q, the longest substring that appears in k documents. LCS is a well-studied problem having a wide range of applications in Bioinformatics: from microarrays to DNA sequences alignments and analysis. This problem has been solved by Hui (2000International Journal of Computer Science and Engineering15 73–76) by using a famous constant-time solution to the Lowest Common Ancestor (LCA) problem in trees coupled with the use of suffix trees.
In this article, we present a simple method for solving the LCS problem by using suffix trees (STs) and classical union-find data structures. In turn, we show how this simple algorithm can be adapted in order to work with other space efficient data structures such as the enhanced suffix arrays (ESA) and the compressed suffix tree.
- Type
- Paper
- Information
- Mathematical Structures in Computer Science , Volume 27 , Special Issue 2: Special Issue: XIV ICTCS , February 2017 , pp. 277 - 295
- Copyright
- Copyright © Cambridge University Press 2015
References
- 3
- Cited by


