Published online by Cambridge University Press: 17 May 2013
We present a categorical model for intuitionistic linear logic in which objects are polynomial diagrams and morphisms are simulation diagrams. The multiplicative structure (tensor product and its adjoint) can be defined in any locally cartesian closed category, but the additive (product and coproduct) and exponential (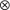 -comonoid comonad) structures require additional properties and are only developed in the category Set, where the objects and morphisms have natural interpretations in terms of games, simulation and strategies.
-comonoid comonad) structures require additional properties and are only developed in the category Set, where the objects and morphisms have natural interpretations in terms of games, simulation and strategies.