Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T00:51:52.952Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalised powerlocales via relation lifting

Published online by Cambridge University Press:  30 August 2012

YDE VENEMA ,
STEVE VICKERS  and
JACOB VOSMAER
YDE VENEMA
Affiliation:
Institute for Logic, Language and Computation, University of Amsterdam, PO Box 94242, 1090 GE Amsterdam, The Netherlands Email: [email protected]
STEVE VICKERS
Affiliation:
School of Computer Science, The University of Birmingham, Birmingham, B15 2TT, United Kingdom Email: [email protected]
JACOB VOSMAER
Affiliation:
Institute for Logic, Language and Computation, University of Amsterdam, PO Box 94242, 1090 GE Amsterdam, The Netherlands Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper introduces an endofunctor VT on the category of frames that is parametrised by an endofunctor T on the category Set that satisfies certain constraints. This generalises Johnstone's construction of the Vietoris powerlocale in the sense that his construction is obtained by taking for T the finite covariant power set functor. Our construction of the T-powerlocale VT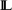 out of a frame 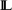is based on ideas from coalgebraic logic and makes explicit the connection between the Vietoris construction and Moss's coalgebraic cover modality.

We show how to extend certain natural transformations between set functors to natural transformations between T-powerlocale functors. Finally, we prove that the operation VT preserves some properties of frames, such as regularity, zero-dimensionality and the combination of zero-dimensionality and compactness.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 23 , Issue 1 , February 2013 , pp. 142 - 199
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aczel, P. (1988) Non-well-founded sets. (With a foreword by Jon Barwise.) CSLI Lecture Notes 14, Stanford University Center for the Study of Language and Information.Google Scholar
Adámek, J. and Trnková, V. (1990) Automata and Algebras in Categories, Kluwer Academic Publishers.Google Scholar
Barwise, J. and Moss, L. (1996) Vicious circles: on the mathematics of non-wellfounded phenomena. CSLI Lecture Notes 60, Stanford University Center for the Study of Language and Information.Google Scholar
Bílková, M., Palmigiano, A. and Venema, Y. (2008) Proof systems for the coalgebraic cover modality. In: Areces, C. and Goldblatt, R. (eds.) Advances in Modal Logic 7, Nancy 2008, College Publications 1–21.Google Scholar
Cîrstea, C., Kurz, A., Pattinson, D., Schröder, L. and Venema, Y. (2009) Modal logics are coalgebraic. The Computer Journal.CrossRefGoogle Scholar
Hermida, C. and Jacobs, B. (1998) Structural induction and coinduction in a fibrational setting. Information and Computation 145 (2)107–152.CrossRefGoogle Scholar
Janin, D. and Walukiewicz, I. (1995) Automata for the modal μ-calculus and related results. In: Mathematical foundations of computer science 1995 (Prague). Springer-Verlag Lecture Notes in Computer Science 969 552–562.CrossRefGoogle Scholar
Johnstone, P. (1982) Stone Spaces, Cambridge Studies in Advanced Mathematics 3, Cambridge University Press.Google Scholar
Johnstone, P. (1985) Vietoris locales and localic semi-lattices. In: Hoffmann, R.-E. (ed.) Continuous Lattices and their Applications. Pure and Applied Mathematics 101 155–18.Google Scholar
Johnstone, P. and Vickers, S. J. (1991) Preframe presentations present. In: Carboni, A., Pedicchio, M. and Rosolini, G. (eds.) Category Theory – Proceedings, Como 1990. Springer-Verlag Lecture Notes in Mathematics 1488 193–212.CrossRefGoogle Scholar
Jung, A., Moshier, M. A. and Vickers, S. J. (2008) Presenting dcpos and dcpo algebras. In: Proceedings of the 24th Conference on the Mathematical Foundations of Programming Semantics (MFPS XXIV). Electronic Notes in Theoretical Computer Science 218 209–229.CrossRefGoogle Scholar
Kissig, C. and Venema, Y. (2009) Complementation of coalgebra automata. In: Kurz, A., Lenisa, M. and Tarlecki, A. (eds.) Algebra and Coalgebra in Computer Science (CALCO 2009). Springer-Verlag Lecture Notes in Computer Science 5728 81–96.CrossRefGoogle Scholar
Kupke, C. (2006) Finitary Coalgebraic Logics, Ph.D. thesis, Institute for Logic, Language and Computation, Universiteit van Amsterdam.Google Scholar
Kupke, C., Kurz, A. and Venema, Y. (2008) Completeness of the finitary Moss logic. In: Areces, C. and Goldblatt, R. (eds.) Advances in Modal Logic 7, Nancy 2008, College Publications 193–217.Google Scholar
Kupke, C., Kurz, A. and Venema, Y. (2010) Completeness for the coalgebraic cover modality (submitted).Google Scholar
MacLane, S. Lane, S. (1998) Categories for the working mathematician, Graduate Texts in Mathematics 2, Springer-Verlag.Google Scholar
Moss, L. (1999) Coalgebraic logic. Annals of Pure and Applied Logic 96 277–317. (Erratum published in Annals of Pure and Applied Logic (1999) 99 241–259.CrossRefGoogle Scholar
Palmigiano, A. and Venema, Y. (2007) Nabla algebras and Chu spaces. In: Mossakowski, T., Montanari, U. and Haveraaen, M. (eds.) Algebra and Coalgebra in Computer Science. Second International Conference, CALCO 2007. Springer-Verlag Lecture Notes in Computer Science 4624 394–408.CrossRefGoogle Scholar
Rutten, J. J. M. M. (2000) Universal coalgebra: a theory of systems. In: Modern algebra and its applications (Nashville, TN). Theoretical Computer Science 249 (1)3–80.CrossRefGoogle Scholar
Street, R. (1972) The formal theory of monads. Journal of Pure and Applied Algebra 2 (2)149–168.CrossRefGoogle Scholar
Trnková, V. (1977) Relational automata in a category and theory of languages. In: Karpinski, M. (ed.) Fundamentals of computation theory: proceedings of the 1977 international FCT-conference. Springer-Verlag Lecture Notes in Computer Science 56 340–355.CrossRefGoogle Scholar
Venema, Y. (2006) Automata and fixed point logic: a coalgebraic perspective. Information and Computation 204 637–678.CrossRefGoogle Scholar
Vickers, S. J. (1989) Topology via logic, Cambridge Tracts in Theoretical Computer Science 5, Cambridge University Press.Google Scholar
Vickers, S. J. (1997) Constructive points of powerlocales. Mathematical Proceedings of the Cambridge Philosophical Society 122 207–222.CrossRefGoogle Scholar
Vickers, S. J. (2006) Compactness in locales and in formal topology. Annals of Pure and Applied Logic 137 (1-3)413–438.CrossRefGoogle Scholar
Vickers, S. J. and Townsend, C. F. (2004) A universal characterization of the double powerlocale. Theoretical Computer Science 316 (1-3)297–321.CrossRefGoogle Scholar
Vietoris, L. (1922) Bereiche zweiter Ordnung. Monatshefte für Mathematik 32 (1)258–280.CrossRefGoogle Scholar