Published online by Cambridge University Press: 11 May 2015
Circular string matching is a problem which naturally arises in many contexts. It consists in finding all occurrences of the rotations of a pattern of length m in a text of length n. There exist optimal worst- and average-case algorithms for circular string matching. Here, we present a suboptimal average-case algorithm for circular string matching requiring time 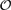 $\mathcal{O}$(n) and space
$\mathcal{O}$(n) and space 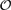 $\mathcal{O}$(m). The importance of our contribution is underlined by the fact that the proposed algorithm can be easily adapted to deal with circular dictionary matching. In particular, we show how the circular dictionary-matching problem can be solved in average-case time
$\mathcal{O}$(m). The importance of our contribution is underlined by the fact that the proposed algorithm can be easily adapted to deal with circular dictionary matching. In particular, we show how the circular dictionary-matching problem can be solved in average-case time 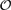 $\mathcal{O}$(n + M) and space
$\mathcal{O}$(n + M) and space 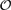 $\mathcal{O}$(M), where M is the total length of the dictionary patterns, assuming that the shortest pattern is sufficiently long. Moreover, the presented average-case algorithms and other worst-case approaches were also implemented. Experimental results, using real and synthetic data, demonstrate that the implementation of the presented algorithms can accelerate the computations by more than a factor of two compared to the corresponding implementation of other approaches.
$\mathcal{O}$(M), where M is the total length of the dictionary patterns, assuming that the shortest pattern is sufficiently long. Moreover, the presented average-case algorithms and other worst-case approaches were also implemented. Experimental results, using real and synthetic data, demonstrate that the implementation of the presented algorithms can accelerate the computations by more than a factor of two compared to the corresponding implementation of other approaches.