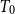1. Introduction
Probabilistic power domain in domain theory plays an important role in modeling the semantics of nondeterministic functional programming languages with probabilistic choice. For example, the universal property of probabilistic power domain can help us define the sequential composition of two programs (Tix et al. Reference Tix, Keimel and Plotkin2009). Saheb-Djahromi (Reference Saheb-Djahromi1980) considered probabilistic power domains over
![]() $\omega$
-algebraic dcpos, Escrig (Reference Escrig1986) studied the case of SFP domains, and Jones (Reference Jones1990) extended the case to general dcpos. It is also shown by Jones and Gordon (Reference Jones and Gordon1989) that the probabilistic power domain of a domain is still a domain and it has a kind of universal property. Kirch (Reference Kirch1993) generalized Jones’ results to extended probabilistic power domain, and Tix (Reference Tix1995) proved that the extended probabilistic power domain of any domain is the free dcpo-cone. However, we show that the extended probabilistic power domain of a dcpo is generally not a free dcpo-cone in this paper. This leads to the question of: what the representation of free dcpo-cone over a non-continuous dcpo is. The aim of this paper is to deal with this problem. We believe that this construction can also be applied to study the algebra of valuation monad over the category of dcpos (Tix et al. Reference Tix, Keimel and Plotkin2009, p. 30).
$\omega$
-algebraic dcpos, Escrig (Reference Escrig1986) studied the case of SFP domains, and Jones (Reference Jones1990) extended the case to general dcpos. It is also shown by Jones and Gordon (Reference Jones and Gordon1989) that the probabilistic power domain of a domain is still a domain and it has a kind of universal property. Kirch (Reference Kirch1993) generalized Jones’ results to extended probabilistic power domain, and Tix (Reference Tix1995) proved that the extended probabilistic power domain of any domain is the free dcpo-cone. However, we show that the extended probabilistic power domain of a dcpo is generally not a free dcpo-cone in this paper. This leads to the question of: what the representation of free dcpo-cone over a non-continuous dcpo is. The aim of this paper is to deal with this problem. We believe that this construction can also be applied to study the algebra of valuation monad over the category of dcpos (Tix et al. Reference Tix, Keimel and Plotkin2009, p. 30).
The intuitive idea of our strategy consists of two steps: the first one is to construct some kind of variation of free cone and the next step is to consider an appropriate completion of this free object. To achieve our goal we will need two tools – directed spaces and D-completions. Directed spaces were introduced independently by Yu and Kou (Reference Yu and Kou2015), which are equivalent to the
![]() $T_0$
monotone-determined spaces defined by Erné (Reference Erné2009). They can be regarded as a topological extended model of domain theory. A monotone determined space is a
$T_0$
monotone-determined spaces defined by Erné (Reference Erné2009). They can be regarded as a topological extended model of domain theory. A monotone determined space is a
![]() $T_0$
space whose topology can be determined by its convergent directed subsets. For instance, every dcpo endowed with the Scott topology is a monotone determined space. The category of monotone determined spaces with continuous maps is a Cartesian closed category, and many properties of dcpos can be extended to monotone determined spaces (Yu and Kou Reference Yu and Kou2015). A natural question arises: what is a monotone determined version of extended probabilistic powerspace over a monotone determined space? To answer this question, we have to do two things. The first one is to define a monotone determined cone by using Keimel’s topological cone (Keimel Reference Keimel2008), just like the d-cone (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003). The second one is to construct a free object over any monotone determined space. We give a concrete construction of extended probabilistic powerspace over any monotone determined space. After that we get a representation of free dcpo-cone over any dcpo L by taking the D-completion of the monotone determined probabilistic powerspace over the Scott space
$T_0$
space whose topology can be determined by its convergent directed subsets. For instance, every dcpo endowed with the Scott topology is a monotone determined space. The category of monotone determined spaces with continuous maps is a Cartesian closed category, and many properties of dcpos can be extended to monotone determined spaces (Yu and Kou Reference Yu and Kou2015). A natural question arises: what is a monotone determined version of extended probabilistic powerspace over a monotone determined space? To answer this question, we have to do two things. The first one is to define a monotone determined cone by using Keimel’s topological cone (Keimel Reference Keimel2008), just like the d-cone (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003). The second one is to construct a free object over any monotone determined space. We give a concrete construction of extended probabilistic powerspace over any monotone determined space. After that we get a representation of free dcpo-cone over any dcpo L by taking the D-completion of the monotone determined probabilistic powerspace over the Scott space
![]() $\Sigma L$
.
$\Sigma L$
.
The paper is organized as follows. In Section 2, we introduce the concept of directed spaces and their properties. In the next section, we define the notion of a monotone determined cone and then give its concrete representation by constructing an appropriate topology on the set of simple valuations. In Section 4, we recall some useful results of D-completion and Scott completion. In addition, we exhibit the free dcpo-cone over any dcpo, which provides an answer to the problem of characterizing the probabilistic power domains of general dcpos. In the final section, we show that the valuation power domain over a dcpo D is not always the free dcpo-cone on D by considering an example by Goubault and Jia (Reference Goubault-Larrecq and Jia2021).
2. Preliminaries
First, we introduce some basic concepts. For basic knowledge and notations in domain theory, topology, and category theory, we refer to Abramsky and Jung (Reference Abramsky, Jung, Abramsky, Gabbay and Maibaum1994), Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003),MacLane (Reference MacLane1971).
Let P be a partially ordered set (poset for short). Given any subset
![]() $A\subseteq P$
, denote
$A\subseteq P$
, denote
![]() $\mathord{\downarrow} A=\{x\in P: \exists a\in A,\ \ x\leq a\}$
,
$\mathord{\downarrow} A=\{x\in P: \exists a\in A,\ \ x\leq a\}$
,
![]() $\mathord{\uparrow} A=\{x\in P: \exists a\in A,\ a\leq x\}$
. We say that A is a lower set (upper set) if
$\mathord{\uparrow} A=\{x\in P: \exists a\in A,\ a\leq x\}$
. We say that A is a lower set (upper set) if
![]() $A=\mathord{\downarrow} A$
(
$A=\mathord{\downarrow} A$
(
![]() $A=\mathord{\uparrow} A$
). A nonempty set
$A=\mathord{\uparrow} A$
). A nonempty set
![]() $D\subseteq P$
is called a directed set if each finite nonempty subset of D has an upper bound in D. A poset P is called a directed complete poset, abbreviated as a dcpo, if each directed subset D of P has a supremum (denoted by
$D\subseteq P$
is called a directed set if each finite nonempty subset of D has an upper bound in D. A poset P is called a directed complete poset, abbreviated as a dcpo, if each directed subset D of P has a supremum (denoted by
![]() $\bigvee D$
). A subset U of a poset P is called a Scott open subset if U is an upper set and for each directed subset
$\bigvee D$
). A subset U of a poset P is called a Scott open subset if U is an upper set and for each directed subset
![]() $D\subseteq P$
such that
$D\subseteq P$
such that
![]() $\bigvee D$
exists and belongs to U,
$\bigvee D$
exists and belongs to U,
![]() $U\cap D\not=\emptyset$
. The set of all Scott open subsets of a poset P form a topology on P, which is called the Scott topology and denoted by
$U\cap D\not=\emptyset$
. The set of all Scott open subsets of a poset P form a topology on P, which is called the Scott topology and denoted by
![]() $\sigma(P)$
. A topological space is called a Scott space if it is a dcpo endowed with the Scott topology. We denote by
$\sigma(P)$
. A topological space is called a Scott space if it is a dcpo endowed with the Scott topology. We denote by
![]() $\Sigma P = (P,\sigma(P))$
. Suppose that P and E are two posets, a map
$\Sigma P = (P,\sigma(P))$
. Suppose that P and E are two posets, a map
![]() $f:P\longrightarrow E$
is called Scott continuous if it is continuous with respect to
$f:P\longrightarrow E$
is called Scott continuous if it is continuous with respect to
![]() $\sigma(P)$
and
$\sigma(P)$
and
![]() $\sigma(E)$
. A poset L is called a complete lattice if any subset has a supremum in L. We say
$\sigma(E)$
. A poset L is called a complete lattice if any subset has a supremum in L. We say
![]() $x\lll y$
in L, if for any set A with
$x\lll y$
in L, if for any set A with
![]() $y\leq\bigvee A$
, there exists some
$y\leq\bigvee A$
, there exists some
![]() $a\in A$
such that
$a\in A$
such that
![]() $x\leq a$
. A complete lattice L is prime continuous if for any
$x\leq a$
. A complete lattice L is prime continuous if for any
![]() $x\in L$
,
$x\in L$
,
![]() $x=\bigvee\{y\in L:y\lll x\}$
.
$x=\bigvee\{y\in L:y\lll x\}$
.
All topological spaces in this paper are supposed to be
![]() $T_0$
spaces. A net in a topological space X is a map
$T_0$
spaces. A net in a topological space X is a map
![]() $\xi: J\longrightarrow X$
, where J is a directed set. Usually, we denote a net by
$\xi: J\longrightarrow X$
, where J is a directed set. Usually, we denote a net by
![]() $(x_j)_{j\in J}$
or
$(x_j)_{j\in J}$
or
![]() $(x_j)$
. We say that
$(x_j)$
. We say that
![]() $(x_j)$
converges to x, denoted by
$(x_j)$
converges to x, denoted by
![]() $(x_j)\rightarrow x$
or
$(x_j)\rightarrow x$
or
![]() $x\equiv \lim x_j$
, if
$x\equiv \lim x_j$
, if
![]() $(x_j)$
is eventually in every open neighborhood of x, that is, for every open neighborhood U of x, there exists
$(x_j)$
is eventually in every open neighborhood of x, that is, for every open neighborhood U of x, there exists
![]() $j_0\in J$
such that for every
$j_0\in J$
such that for every
![]() $j\in J$
,
$j\in J$
,
![]() $j\geq j_0\Rightarrow x_j\in U$
.
$j\geq j_0\Rightarrow x_j\in U$
.
Let X be a
![]() $T_{0}$
topological space with its topology denoted by
$T_{0}$
topological space with its topology denoted by
![]() $\mathcal{O}(X)$
. Then, the specialization order on X is defined as follows:
$\mathcal{O}(X)$
. Then, the specialization order on X is defined as follows:
where
![]() $\overline{\{y\}}$
denotes the closure of
$\overline{\{y\}}$
denotes the closure of
![]() $\{y\}$
. From now on, the order of a
$\{y\}$
. From now on, the order of a
![]() $T_{0}$
topological space always indicates the specialization order “
$T_{0}$
topological space always indicates the specialization order “
![]() $\sqsubseteq$
”.
$\sqsubseteq$
”.
Supposing that X is a
![]() $T_{0}$
space, then every directed set
$T_{0}$
space, then every directed set
![]() $D\subseteq X$
can be regarded as a net
$D\subseteq X$
can be regarded as a net
![]() $(d)_{d \in D}$
in X. We use
$(d)_{d \in D}$
in X. We use
![]() $D\rightarrow x$
or
$D\rightarrow x$
or
![]() $x\equiv \lim D$
to represent that D converges to x. Define
$x\equiv \lim D$
to represent that D converges to x. Define
It is easy to verify that, for every
![]() $x, y\in X$
,
$x, y\in X$
,
![]() $x\sqsubseteq y\Longleftrightarrow \{y\}\rightarrow x$
. Therefore, if
$x\sqsubseteq y\Longleftrightarrow \{y\}\rightarrow x$
. Therefore, if
![]() $x\sqsubseteq y$
then
$x\sqsubseteq y$
then
![]() $(\{y\},\ x)\in D(X)$
. Next, we introduce the concept of monotone determined spaces.
$(\{y\},\ x)\in D(X)$
. Next, we introduce the concept of monotone determined spaces.
Definition 1. (Yu and Kou Reference Yu and Kou2015) Let X be a
![]() $T_{0}$
space.
$T_{0}$
space.
-
(1) A subset U of X is called a directed open set if
 $\forall (D,\ x)\in D(X),\ x\in U \Rightarrow D\cap U\neq \emptyset$
. Denote the set of all directed open subsets of X by d(X).
$\forall (D,\ x)\in D(X),\ x\in U \Rightarrow D\cap U\neq \emptyset$
. Denote the set of all directed open subsets of X by d(X). -
(2) X is called a monotone determined space if each directed open subset of X is an open subset, that is,
 $d(X)= \mathcal{O}(X)$
.
$d(X)= \mathcal{O}(X)$
.
Dcpos endowed with the Scott topology are monotone determined spaces and many properties of dcpos can be extended to monotone determined spaces. The topology on a monotone determined space need not be Scott topology; for example, every poset with the Alexanderoff topology is a monotone determined space. The natural numbers with co-finite topology are not a monotone determined space. For more details, we refer to Yu and Kou (Reference Yu and Kou2015).
Monotone determined spaces with continuous maps as morphisms form a Cartesian closed category, denoted by Dtop. In the following, we introduce the representation and some basic properties of categorical product of monotone determined spaces in
![]() $\bf Dtop$
.
$\bf Dtop$
.
Suppose that
![]() $X,\ Y$
are two monotone determined spaces. Let
$X,\ Y$
are two monotone determined spaces. Let
![]() $X\times Y$
be the Cartesian product of X and Y, then we have a natural partial order on it:
$X\times Y$
be the Cartesian product of X and Y, then we have a natural partial order on it:
![]() $\forall (x_{1}, y_{1}), (x_{2}, y_{2})\in X\times Y$
,
$\forall (x_{1}, y_{1}), (x_{2}, y_{2})\in X\times Y$
,
which is called the pointwise order on
![]() $X\times Y$
. Now, we define a topological space
$X\times Y$
. Now, we define a topological space
![]() $X\otimes Y$
as follows:
$X\otimes Y$
as follows:
-
(1) The underlying set of
 $X\otimes Y$
is
$X\otimes Y$
is
 $X\times Y$
;
$X\times Y$
; -
(2) The topology on
 $X\otimes Y$
is generated as follows: for each given
$X\otimes Y$
is generated as follows: for each given
 $\leq$
- directed set
$\leq$
- directed set
 $D\subseteq X\times Y$
and
$D\subseteq X\times Y$
and
 $(x, y)\in X\times Y$
, define A subset
$(x, y)\in X\times Y$
, define A subset \[D\rightarrow_d(x, y)\in X\otimes Y\iff\pi_{1}D\rightarrow x\in X,\ \pi_{2}D\rightarrow y\in Y. \]
\[D\rightarrow_d(x, y)\in X\otimes Y\iff\pi_{1}D\rightarrow x\in X,\ \pi_{2}D\rightarrow y\in Y. \]
 $U\subseteq X\otimes Y$
is open iff for every
$U\subseteq X\otimes Y$
is open iff for every
 $D\rightarrow_d (x, y)$
as defined above,
$D\rightarrow_d (x, y)$
as defined above,
 $(x, y)\in U\Longrightarrow U\cap D\neq\emptyset$
.
$(x, y)\in U\Longrightarrow U\cap D\neq\emptyset$
.
Theorem 2. (Yu and Kou Reference Yu and Kou2015) Let X and Y be two monotone determined spaces.
-
(1) The topological space
 $X\otimes Y$
defined as above is a monotone determined space, and the specialization order on
$X\otimes Y$
defined as above is a monotone determined space, and the specialization order on
 $X\otimes Y$
is equal to the pointwise order on
$X\otimes Y$
is equal to the pointwise order on
 $X\times Y$
.
$X\times Y$
. -
(2) Let Z be a monotone determined space. Then
 $f:X\otimes Y\longrightarrow Z$
is continuous if and only if it is continuous in each argument separately.
$f:X\otimes Y\longrightarrow Z$
is continuous if and only if it is continuous in each argument separately.
Definition 3. Let
![]() $X,\ Y$
be two
$X,\ Y$
be two
![]() $T_{0}$
spaces. A map
$T_{0}$
spaces. A map
![]() $f:X\longrightarrow Y$
is called directed continuous if it is monotone and preserves all limits of directed subsets of X, that is,
$f:X\longrightarrow Y$
is called directed continuous if it is monotone and preserves all limits of directed subsets of X, that is,
![]() $(D, x)\in D(X)\Rightarrow(f(D),f(x))\in D(Y)$
.
$(D, x)\in D(X)\Rightarrow(f(D),f(x))\in D(Y)$
.
Proposition 4. (Yu and Kou Reference Yu and Kou2015) Let
![]() $X,\ Y$
be two
$X,\ Y$
be two
![]() $T_{0}$
spaces, and
$T_{0}$
spaces, and
![]() $f:X\longrightarrow Y$
be a map from X to Y.
$f:X\longrightarrow Y$
be a map from X to Y.
-
(1) f is directed continuous if and only if
 $\forall U\in d(Y),\ f^{-1}(U)\in d(X)$
.
$\forall U\in d(Y),\ f^{-1}(U)\in d(X)$
. -
(2) If
 $X,\ Y$
are monotone determined spaces, then f is continuous if and only if it is directed continuous.
$X,\ Y$
are monotone determined spaces, then f is continuous if and only if it is directed continuous.
Let P be a dcpo, and
![]() $x,\ y\in P$
. We say that x is way-below y, if for each given directed set
$x,\ y\in P$
. We say that x is way-below y, if for each given directed set
![]() $D\subseteq P$
,
$D\subseteq P$
,
![]() $y\leq\bigvee D$
implies that there exists some
$y\leq\bigvee D$
implies that there exists some
![]() $d\in D$
such that
$d\in D$
such that
![]() $x\leq d$
. We write
$x\leq d$
. We write ![]()
Definition 5. A dcpo P is called a domain if for each
![]() $x\in P$
,
$x\in P$
, ![]() x is directed and
x is directed and ![]()
A
![]() $T_0$
topological space X is a c-space if for each
$T_0$
topological space X is a c-space if for each
![]() $x\in X$
and each open neighborhood U of x, there exists some
$x\in X$
and each open neighborhood U of x, there exists some
![]() $y\in U$
such that
$y\in U$
such that
![]() $x\in ({\uparrow y})^\circ \subseteq U$
. The c-spaces are classical spaces investigated by many scholars. Continuous domains endowed with the Scott topology are c-spaces, and c-spaces are monotone determined spaces (Erné Reference Erné2009).
$x\in ({\uparrow y})^\circ \subseteq U$
. The c-spaces are classical spaces investigated by many scholars. Continuous domains endowed with the Scott topology are c-spaces, and c-spaces are monotone determined spaces (Erné Reference Erné2009).
The following result gives a characterization of c-space.
Proposition 6. (Goubault-Larrecq Reference Goubault-Larrecq2013, Lemmas 8.3.41, 8.3.42) A
![]() $T_0$
space is a c-space iff the lattice
$T_0$
space is a c-space iff the lattice
![]() $\mathcal{O}(X)$
with the inclusion order is prime continuous.
$\mathcal{O}(X)$
with the inclusion order is prime continuous.
3. The Monotone Determined Probabilistic Powerspaces
As mentioned above, monotone determined spaces form a very natural topological extended model of dcpos in Domain theory. Like the work done by Battenfeld and Schöder (1994), extending the power domain to the category of monotone determined spaces is useful. In this section, we will construct the monotone determined probabilistic powerspace of an arbitrary monotone determined space, which is a free algebra generated by the addition and scalar multiplication over the monotone determined space.
Definition 7. (Heckmann Reference Heckmann, Andima, Flagg, Itzkowitz, Misra, Kong and Kopperman1996) Let X be a topological space. A map
![]() $\mu:\mathcal{O}(X)\longrightarrow[0, +\infty]$
is called a continuous valuation if the following hold:
$\mu:\mathcal{O}(X)\longrightarrow[0, +\infty]$
is called a continuous valuation if the following hold:
-
(1) strictness:
 $\mu(\emptyset)=0$
;
$\mu(\emptyset)=0$
; -
(2) monotonicity:
 $\forall V\subseteq U\in\mathcal{O}(X)$
$\forall V\subseteq U\in\mathcal{O}(X)$
 $\implies$
$\implies$
 $\mu(V)\leq\mu(U)$
;
$\mu(V)\leq\mu(U)$
; -
(3) modular law:
 $\mu(U)+\mu(V)=\mu(U\cup V)+\mu(U\cap V), \forall U,V\in\mathcal{O}(X)$
;
$\mu(U)+\mu(V)=\mu(U\cup V)+\mu(U\cap V), \forall U,V\in\mathcal{O}(X)$
; -
(4) continuity: for each directed subset
 $\mathcal{D}$
, also called a directed family of
$\mathcal{D}$
, also called a directed family of
 $\mathcal{O}(X)$
,
$\mathcal{O}(X)$
,
 $\mu(\sup\mathcal{D})=\sup\{\mu(U):U\in\mathcal{D}\}$
.
$\mu(\sup\mathcal{D})=\sup\{\mu(U):U\in\mathcal{D}\}$
.
![]() $\mathcal{V}(X)$
stands for the set of continuous valuations over X.
$\mathcal{V}(X)$
stands for the set of continuous valuations over X.
Definition 8. (Heckmann Reference Heckmann, Andima, Flagg, Itzkowitz, Misra, Kong and Kopperman1996) A continuous valuation
![]() $\mu$
is called a point-continuous valuation if for any non-negative real number r and any open set U of X with
$\mu$
is called a point-continuous valuation if for any non-negative real number r and any open set U of X with
![]() $\mu(U)>r$
, there is a finite set
$\mu(U)>r$
, there is a finite set
![]() $F\subseteq U$
such that
$F\subseteq U$
such that
![]() $\mu(V)>r$
for any open set
$\mu(V)>r$
for any open set
![]() $V\supseteq F$
. Let
$V\supseteq F$
. Let
![]() $\mathcal{V}_{p}(X)$
denote the set of all point-continuous valuations over X.
$\mathcal{V}_{p}(X)$
denote the set of all point-continuous valuations over X.
Definition 9. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Definition IV-9.9) Let X be a topological space. For each
![]() $x\in X$
, we define the point valuation
$x\in X$
, we define the point valuation
![]() $\eta_x:\mathcal{O}(X)\longrightarrow [0,+\infty]$
as follows:
$\eta_x:\mathcal{O}(X)\longrightarrow [0,+\infty]$
as follows:
![]() $\eta_x(U)=1$
if
$\eta_x(U)=1$
if
![]() $x\in U$
, and
$x\in U$
, and
![]() $\eta_x(U)=0$
if
$\eta_x(U)=0$
if
![]() $x\notin U$
. A finite linear sum
$x\notin U$
. A finite linear sum
![]() $\xi=\sum_{b\in B}r_b\eta_b$
with
$\xi=\sum_{b\in B}r_b\eta_b$
with
![]() $0< r_b < +\infty$
, defined by
$0< r_b < +\infty$
, defined by
![]() $\xi(U)=\sum_{b\in U}r_b$
, is called a simple valuation. The set
$\xi(U)=\sum_{b\in U}r_b$
, is called a simple valuation. The set
![]() $B=\text{supp}\xi$
is called the support of
$B=\text{supp}\xi$
is called the support of
![]() $\xi$
. We denote the set of all simple valuations by
$\xi$
. We denote the set of all simple valuations by
![]() $\mathcal{V}_{f}(X)$
.
$\mathcal{V}_{f}(X)$
.
The following lemma shows that every simple valuation has a unique representation as a linear combination of point valuations.
Lemma 10. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Lemma IV-9.22) Let
![]() $\zeta=\sum_{b\in B}r_b\eta_b$
and
$\zeta=\sum_{b\in B}r_b\eta_b$
and
![]() $\sum_{c\in C}s_c\eta_c=\xi$
be two simple valuations on
$\sum_{c\in C}s_c\eta_c=\xi$
be two simple valuations on
![]() $\mathcal{O}(X)$
, where X is a
$\mathcal{O}(X)$
, where X is a
![]() $T_0$
space. If
$T_0$
space. If
![]() $\xi$
and
$\xi$
and
![]() $\zeta$
are distinct as linear combinations, then they are distinct as valuations.
$\zeta$
are distinct as linear combinations, then they are distinct as valuations.
Topological cones were defined by Keimel (Reference Keimel2008). In the following, we replace the
![]() $T_0$
space by monotone determined space to give the definition of monotone determined cone.
$T_0$
space by monotone determined space to give the definition of monotone determined cone.
Definition 11. A monotone determined cone is a monotone determined space X equipped with a distinguished element
![]() $0\in X$
, an addition
$0\in X$
, an addition
![]() $+:X\otimes X\rightarrow X$
, and a scalar multiplication
$+:X\otimes X\rightarrow X$
, and a scalar multiplication
![]() $\cdot:\mathbb{R}^+\otimes X\rightarrow X$
(
$\cdot:\mathbb{R}^+\otimes X\rightarrow X$
(
![]() $\mathbb{R}^+$
endowed with the Scott topology in its usual partial order) such that both operations are continuous and the following are satisfied.
$\mathbb{R}^+$
endowed with the Scott topology in its usual partial order) such that both operations are continuous and the following are satisfied.
-
(1)
 $x+y=y+x$
,
$x+y=y+x$
,
 $\forall x,\ y\in X$
,
$\forall x,\ y\in X$
, -
(2)
 $(x+y)+z=x+(y+z)$
,
$(x+y)+z=x+(y+z)$
,
 $\forall x,\ y,\ z\in X$
,
$\forall x,\ y,\ z\in X$
, -
(3)
 $0+x=x,\ \forall x\in X$
,
$0+x=x,\ \forall x\in X$
, -
(4)
 $(kl)\cdot x=k\cdot(l\cdot x),\ \forall k,\ l\in\mathbb{R}^+,\forall x\in X$
,
$(kl)\cdot x=k\cdot(l\cdot x),\ \forall k,\ l\in\mathbb{R}^+,\forall x\in X$
, -
(5)
 $(k+l)\cdot x=(k\cdot x)+(l\cdot x)$
,
$(k+l)\cdot x=(k\cdot x)+(l\cdot x)$
,
 $\forall k,\ l\in\mathbb{R}^+,\ \forall x\in X$
,
$\forall k,\ l\in\mathbb{R}^+,\ \forall x\in X$
, -
(6)
 $k\cdot(x+y)=(k\cdot x)+(k\cdot y),\ \forall k\in\mathbb{R^+},\ \forall x,\ y\in X$
,
$k\cdot(x+y)=(k\cdot x)+(k\cdot y),\ \forall k\in\mathbb{R^+},\ \forall x,\ y\in X$
, -
(7)
 $1\cdot x=x,\ \forall x\in X$
,
$1\cdot x=x,\ \forall x\in X$
, -
(8)
 $k\cdot 0=0$
,
$k\cdot 0=0$
,
 $\forall k\in\mathbb{R}^+$
.
$\forall k\in\mathbb{R}^+$
.
Definition 12. Let
![]() $(X, +, \cdot)$
,
$(X, +, \cdot)$
,
![]() $(Y, \uplus, \ast)$
be two monotone determined cones. A map
$(Y, \uplus, \ast)$
be two monotone determined cones. A map
![]() $f:(X, +, \cdot)\rightarrow (Y, \uplus, \ast)$
is called a monotone determined cone homomorphism between X and Y, if f is continuous and
$f:(X, +, \cdot)\rightarrow (Y, \uplus, \ast)$
is called a monotone determined cone homomorphism between X and Y, if f is continuous and
![]() $f(x+ y)=f(x)\uplus f(y)$
and
$f(x+ y)=f(x)\uplus f(y)$
and
![]() $f(a\cdot x)=a\ast f(x)$
hold for all
$f(a\cdot x)=a\ast f(x)$
hold for all
![]() $x, y\in X$
, and
$x, y\in X$
, and
![]() $a\in\mathbb{R}^+=[0,+\infty)$
.
$a\in\mathbb{R}^+=[0,+\infty)$
.
Denote the category of all monotone determined cones and monotone determined cone homomorphisms by Dscone. Then Dscone is a subcategory of Dtop. Now, we define the notion of monotone determined probabilistic powerspaces.
Definition 13. Let X be a monotone determined space. A monotone determined cone
![]() $(Z,+,\cdot)$
is called the monotone determined probabilistic powerspace of X if there is a continuous map
$(Z,+,\cdot)$
is called the monotone determined probabilistic powerspace of X if there is a continuous map
![]() $i:X\longrightarrow Z$
that satisfies the following property: for arbitrary monotone determined cone
$i:X\longrightarrow Z$
that satisfies the following property: for arbitrary monotone determined cone
![]() $(Y,\ \uplus,\ \ast)$
and continuous map
$(Y,\ \uplus,\ \ast)$
and continuous map
![]() $f:X\longrightarrow Y$
, there exists a unique monotone determined cone homomorphism
$f:X\longrightarrow Y$
, there exists a unique monotone determined cone homomorphism
![]() $\bar{f}:(Z,\ +,\ \cdot)\rightarrow (Y,\ \uplus,\ \ast)$
such that
$\bar{f}:(Z,\ +,\ \cdot)\rightarrow (Y,\ \uplus,\ \ast)$
such that
![]() $f=\bar{f}\circ i$
.
$f=\bar{f}\circ i$
.
By the definition above, if monotone determined cones
![]() $(Z_1, +, \cdot)$
and
$(Z_1, +, \cdot)$
and
![]() $(Z_2, \uplus, \ast)$
are both the monotone determined probabilistic powerspaces of X, then there exists a topological homomorphism which is also a monotone determined cone homomorphism
$(Z_2, \uplus, \ast)$
are both the monotone determined probabilistic powerspaces of X, then there exists a topological homomorphism which is also a monotone determined cone homomorphism
![]() $g:Z_1\rightarrow Z_2$
. Therefore, up to isomorphism, the monotone determined probabilistic powerspace of a monotone determined space is unique. Hence, we denote the monotone determined probabilistic powerspace of each monotone determined space X by
$g:Z_1\rightarrow Z_2$
. Therefore, up to isomorphism, the monotone determined probabilistic powerspace of a monotone determined space is unique. Hence, we denote the monotone determined probabilistic powerspace of each monotone determined space X by
![]() $P_D(X)$
.
$P_D(X)$
.
Now, we show the existence of monotone determined probabilistic powerspaces by giving the concrete construction of the monotone determined probabilistic powerspace of any monotone determined space X.
For any monotone determined space X, there is a natural pointwise order
![]() $\leq$
on
$\leq$
on
![]() $\mathcal{V}_f(X)$
:
$\mathcal{V}_f(X)$
:
In the following, we will introduce a new convergence on the set of simple valuations.
Definition 14. Let
![]() $\mathcal{D}=\{\xi_i\}_{i\in I} $
be a directed subset of
$\mathcal{D}=\{\xi_i\}_{i\in I} $
be a directed subset of
![]() $\mathcal{V}_f(X)$
in the pointwise order and
$\mathcal{V}_f(X)$
in the pointwise order and
![]() $\xi\in \mathcal{V}_f(X)$
with nonempty support. We write
$\xi\in \mathcal{V}_f(X)$
with nonempty support. We write
![]() $\mathcal{D}\Rightarrow_P \xi$
if there is a representation of
$\mathcal{D}\Rightarrow_P \xi$
if there is a representation of
![]() $\xi$
as
$\xi$
as
![]() $\sum_{i=1}^n r_{b_i}\eta_{b_i}$
(
$\sum_{i=1}^n r_{b_i}\eta_{b_i}$
(
![]() $r_{b_i}>0$
for each i,
$r_{b_i}>0$
for each i,
![]() $b_i$
may be equal to
$b_i$
may be equal to
![]() $b_j$
for
$b_j$
for
![]() $i\neq j$
), and there exist directed subsets
$i\neq j$
), and there exist directed subsets
![]() $D_1,\cdots,D_n\subseteq X$
satisfying
$D_1,\cdots,D_n\subseteq X$
satisfying
![]() $\forall i\in\{1,\cdots,n\}: D_i\rightarrow b_i$
in X, such that for any
$\forall i\in\{1,\cdots,n\}: D_i\rightarrow b_i$
in X, such that for any
![]() $(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$
and
$(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$
and
![]() $r_{b_i}'<r_{b_i}$
(for
$r_{b_i}'<r_{b_i}$
(for
![]() $i=1,\dots,n$
), there exists some
$i=1,\dots,n$
), there exists some
![]() $\xi'\in\mathcal{D}$
such that
$\xi'\in\mathcal{D}$
such that
![]() $\sum_{i=1}^{n} r_{b_i}'\eta_{d_i}\leq\xi'$
. If the support of
$\sum_{i=1}^{n} r_{b_i}'\eta_{d_i}\leq\xi'$
. If the support of
![]() $\xi$
is
$\xi$
is
![]() $\emptyset$
, then
$\emptyset$
, then
![]() $\xi=0$
. We define that any directed subset of
$\xi=0$
. We define that any directed subset of
![]() $\mathcal{V}_f(X)$
always converges to 0.
$\mathcal{V}_f(X)$
always converges to 0.
A subset
![]() $\mathcal{U}\subseteq \mathcal{V}_f(X)$
is called a
$\mathcal{U}\subseteq \mathcal{V}_f(X)$
is called a
![]() $\Rightarrow_P$
convergence open subset of
$\Rightarrow_P$
convergence open subset of
![]() $\mathcal{V}_f(X)$
if and only if for each directed subset
$\mathcal{V}_f(X)$
if and only if for each directed subset
![]() $\mathcal{D}$
of
$\mathcal{D}$
of
![]() $\mathcal{V}_f(X)$
and
$\mathcal{V}_f(X)$
and
![]() $\xi\in \mathcal{V}_f(X)$
,
$\xi\in \mathcal{V}_f(X)$
,
![]() $\mathcal{D}\Rightarrow_{P}\xi\in \mathcal{U}$
implies
$\mathcal{D}\Rightarrow_{P}\xi\in \mathcal{U}$
implies
![]() $\mathcal{D}\cap \mathcal{U}\neq \emptyset$
. Denote the set of all
$\mathcal{D}\cap \mathcal{U}\neq \emptyset$
. Denote the set of all
![]() $\Rightarrow_P$
convergence open subsets of
$\Rightarrow_P$
convergence open subsets of
![]() $\mathcal{V}_f(X)$
by
$\mathcal{V}_f(X)$
by
![]() $O_{\Rightarrow_{P}}(\mathcal{V}_f(X))$
.
$O_{\Rightarrow_{P}}(\mathcal{V}_f(X))$
.
Proposition 15. Let X be a monotone determined space. Then, the following statements hold.
-
(1)
 $(\mathcal{V}_f(X),\ O_{\Rightarrow_P}(\mathcal{V}_f(X)))$
is a topological space, henceforth, denoted as CX.
$(\mathcal{V}_f(X),\ O_{\Rightarrow_P}(\mathcal{V}_f(X)))$
is a topological space, henceforth, denoted as CX. -
(2) The specialization order
 $\sqsubseteq $
on CX is equal to the pointwise order.
$\sqsubseteq $
on CX is equal to the pointwise order. -
(3) CX is a monotone determined space, that is,
 $O_{\Rightarrow_P}(\mathcal{V}_f(X))=d(CX)$
.
$O_{\Rightarrow_P}(\mathcal{V}_f(X))=d(CX)$
.
Proof. (1) Obviously,
![]() $\emptyset,\ CX\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
. Suppose that
$\emptyset,\ CX\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
. Suppose that
![]() $\mathcal{U}\in O_{\Rightarrow_U}(\mathcal{V}_f(X)$
),
$\mathcal{U}\in O_{\Rightarrow_U}(\mathcal{V}_f(X)$
),
![]() $\xi\leq\eta$
,
$\xi\leq\eta$
,
![]() $\xi\in\mathcal{U}$
, and
$\xi\in\mathcal{U}$
, and
![]() $\xi=\sum_{i=1}^{n}r_{b_{i}}\eta_{b_i}$
. Then, it is evident that
$\xi=\sum_{i=1}^{n}r_{b_{i}}\eta_{b_i}$
. Then, it is evident that
![]() $\{\eta\}\Rightarrow_{P}\xi$
, since we only need to take
$\{\eta\}\Rightarrow_{P}\xi$
, since we only need to take
![]() $D_{i}=\{b_{i}\}$
for
$D_{i}=\{b_{i}\}$
for
![]() $\ i=1,\dots,n$
. Then,
$\ i=1,\dots,n$
. Then,
![]() $\{\eta\}\cap \mathcal{U} \neq \emptyset$
, this means
$\{\eta\}\cap \mathcal{U} \neq \emptyset$
, this means
![]() $\eta\in \mathcal{U}$
, and thus
$\eta\in \mathcal{U}$
, and thus
![]() $\mathcal{U}$
is an upper set with respect to the pointwise order
$\mathcal{U}$
is an upper set with respect to the pointwise order
![]() $\leq$
.
$\leq$
.
Let
![]() $\mathcal{U}_{1},\mathcal{U}_{2}\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
, and
$\mathcal{U}_{1},\mathcal{U}_{2}\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
, and
![]() $\mathcal D$
be a directed subset of
$\mathcal D$
be a directed subset of
![]() $\mathcal{V}_f(X)$
with
$\mathcal{V}_f(X)$
with
![]() $\mathcal{D}\Rightarrow_{P} \xi\in \mathcal{U}_{1}\cap\mathcal{U}_{2}$
. Then, there exists some
$\mathcal{D}\Rightarrow_{P} \xi\in \mathcal{U}_{1}\cap\mathcal{U}_{2}$
. Then, there exists some
![]() $\xi_{1}\in \mathcal{D}\cap \mathcal{U}_{1}$
and
$\xi_{1}\in \mathcal{D}\cap \mathcal{U}_{1}$
and
![]() $ \xi_{2}\in \mathcal{D}\cap \mathcal{U}_{2}$
. Since
$ \xi_{2}\in \mathcal{D}\cap \mathcal{U}_{2}$
. Since
![]() $\mathcal{D}$
is directed, there exists some
$\mathcal{D}$
is directed, there exists some
![]() $\xi_{3}\in \mathcal{D}$
such that
$\xi_{3}\in \mathcal{D}$
such that
![]() $\xi_{3}\geq\xi_{1},\ \xi_{2}$
. Then,
$\xi_{3}\geq\xi_{1},\ \xi_{2}$
. Then,
![]() $\xi_{3}\in \mathcal{D}\cap \mathcal{U}_{1}\cap\mathcal{U}_{2}$
, and then
$\xi_{3}\in \mathcal{D}\cap \mathcal{U}_{1}\cap\mathcal{U}_{2}$
, and then
![]() $\mathcal{U}_{1}\cap\mathcal{U}_{2} \in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
. In the same way, we can show that
$\mathcal{U}_{1}\cap\mathcal{U}_{2} \in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
. In the same way, we can show that
![]() $O_{\Rightarrow_U}(\mathcal{V}_f(X))$
is closed under arbitrary unions. Hence,
$O_{\Rightarrow_U}(\mathcal{V}_f(X))$
is closed under arbitrary unions. Hence,
![]() $O_{\Rightarrow_U}(\mathcal{V}_f(X))$
is a topology.
$O_{\Rightarrow_U}(\mathcal{V}_f(X))$
is a topology.
(2) By the proof of (1), each
![]() $\Rightarrow_P$
convergence open set is an upper set with respect to the pointwise order. We only need to prove that
$\Rightarrow_P$
convergence open set is an upper set with respect to the pointwise order. We only need to prove that
![]() $\downarrow_{\leq}\eta$
is a closed set in CX. Equivalently, we show that
$\downarrow_{\leq}\eta$
is a closed set in CX. Equivalently, we show that
![]() $CX\setminus\downarrow_{\leq}\eta$
is a
$CX\setminus\downarrow_{\leq}\eta$
is a
![]() $\Rightarrow_{P}$
convergence open set.
$\Rightarrow_{P}$
convergence open set.
Set
![]() $\mathcal{U}=CX\setminus\downarrow_{\leq}\eta$
and
$\mathcal{U}=CX\setminus\downarrow_{\leq}\eta$
and
![]() $\mathcal{D}\Rightarrow_{P}\xi\in\mathcal{U}$
. To obtain a contradiction, suppose
$\mathcal{D}\Rightarrow_{P}\xi\in\mathcal{U}$
. To obtain a contradiction, suppose
![]() $\mathcal{U}\cap\mathcal{D}=\emptyset$
, that is,
$\mathcal{U}\cap\mathcal{D}=\emptyset$
, that is,
![]() $\forall\xi'\in\mathcal{D},\xi'\leq\eta$
. By the definition of
$\forall\xi'\in\mathcal{D},\xi'\leq\eta$
. By the definition of
![]() $\mathcal{D}\Rightarrow_{P}\xi$
, there is a representation
$\mathcal{D}\Rightarrow_{P}\xi$
, there is a representation
![]() $\xi=\sum_{i=1}^{n}r_{b_{i}}\eta_{b_i}$
, and we have directed sets
$\xi=\sum_{i=1}^{n}r_{b_{i}}\eta_{b_i}$
, and we have directed sets
![]() $D_1,\dots,D_n\subseteq X$
with
$D_1,\dots,D_n\subseteq X$
with
![]() $D_i\rightarrow b_i,i=1,\dots,n$
, and for any
$D_i\rightarrow b_i,i=1,\dots,n$
, and for any
![]() $ (d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$
and any
$ (d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$
and any
![]() $r_{b_{i}}'<r_{b_{i}} (1\leq i\leq n)$
, there exists some
$r_{b_{i}}'<r_{b_{i}} (1\leq i\leq n)$
, there exists some
![]() $\xi'\in\mathcal{D}$
such that
$\xi'\in\mathcal{D}$
such that
![]() $\sum_{i=1}^{n} r_{b_i}'\eta_{d_i}\leq\xi'$
. Now, we claim that
$\sum_{i=1}^{n} r_{b_i}'\eta_{d_i}\leq\xi'$
. Now, we claim that
![]() $\xi\leq\eta$
, which contradicts
$\xi\leq\eta$
, which contradicts
![]() $\xi\in\mathcal{U}$
. By the definition of pointwise order
$\xi\in\mathcal{U}$
. By the definition of pointwise order
![]() $\leq$
, for any
$\leq$
, for any
![]() $ U\in\mathcal{O}(X)$
, we may assume that
$ U\in\mathcal{O}(X)$
, we may assume that
![]() $b_1,\dots,b_k\in U,0\leq k\leq n$
. Since
$b_1,\dots,b_k\in U,0\leq k\leq n$
. Since
![]() $D_i\rightarrow b_i,i=1,\dots,k$
, there exists
$D_i\rightarrow b_i,i=1,\dots,k$
, there exists
![]() $(d_1,\dots,d_k)\in\prod_{i=1}^{k}D_i$
such that
$(d_1,\dots,d_k)\in\prod_{i=1}^{k}D_i$
such that
![]() $d_i\in U$
. For each
$d_i\in U$
. For each
![]() $r_{b_{i}}'<r_{b_{i}},i=1,\dots,k$
, there exists
$r_{b_{i}}'<r_{b_{i}},i=1,\dots,k$
, there exists
![]() $\xi'\in\mathcal{D}$
such that
$\xi'\in\mathcal{D}$
such that
![]() $\sum_{i=1}^{k} r_{b_i}'\eta_{d_i}\leq\xi'$
. Note that
$\sum_{i=1}^{k} r_{b_i}'\eta_{d_i}\leq\xi'$
. Note that
![]() $k\leq n$
, then,
$k\leq n$
, then,
 \[\left(\sum_{i=1}^{k} r_{b_i}'\eta_{b_i}\right)(U)=\sum_{i=1}^{k} r_{b_i}'\leq\xi'(U)\leq\eta(U).\]
\[\left(\sum_{i=1}^{k} r_{b_i}'\eta_{b_i}\right)(U)=\sum_{i=1}^{k} r_{b_i}'\leq\xi'(U)\leq\eta(U).\]
But the supremum of the left hand side is
![]() $\sum_{i=1}^{k} r_{b_i}=(\sum_{i=1}^{k}r_{b_{i}}\eta_{b_i})(U)=\xi(U)$
.
$\sum_{i=1}^{k} r_{b_i}=(\sum_{i=1}^{k}r_{b_{i}}\eta_{b_i})(U)=\xi(U)$
.
(3) For an arbitrary topological space X,
![]() $\mathcal{O}(X)\subseteq d(X)$
holds. Thus,
$\mathcal{O}(X)\subseteq d(X)$
holds. Thus,
![]() $O_{\Rightarrow_P}(\mathcal{V}_f(X))\subseteq d(CX)$
. On the other hand, according to the definition of
$O_{\Rightarrow_P}(\mathcal{V}_f(X))\subseteq d(CX)$
. On the other hand, according to the definition of
![]() $\Rightarrow_P$
convergence topology, if
$\Rightarrow_P$
convergence topology, if
![]() $\mathcal D\subseteq CX$
is directed and
$\mathcal D\subseteq CX$
is directed and
![]() $ \mathcal{D}\Rightarrow_{P}\xi$
, then
$ \mathcal{D}\Rightarrow_{P}\xi$
, then
![]() $\mathcal{D}$
converges to
$\mathcal{D}$
converges to
![]() $\xi$
with respect to
$\xi$
with respect to
![]() $O_{\Rightarrow_P}(\mathcal{V}_f(X))$
. By the definition of directed open set,
$O_{\Rightarrow_P}(\mathcal{V}_f(X))$
. By the definition of directed open set,
![]() $\mathcal{D}\Rightarrow_{P}\xi \in\mathcal{U}\in d(CX)$
will imply
$\mathcal{D}\Rightarrow_{P}\xi \in\mathcal{U}\in d(CX)$
will imply
![]() $\mathcal{U}\cap \mathcal{D}\neq \emptyset$
. Then,
$\mathcal{U}\cap \mathcal{D}\neq \emptyset$
. Then,
![]() $\mathcal{U}\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
, it follows that
$\mathcal{U}\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
, it follows that
![]() $O_{\Rightarrow_P}(\mathcal{V}_f(X))= d(CX)$
, that is, CX is a monotone determined space.
$O_{\Rightarrow_P}(\mathcal{V}_f(X))= d(CX)$
, that is, CX is a monotone determined space.
Proposition 16. Suppose that
![]() $X,\ Y$
are two monotone determined spaces. Then, a map
$X,\ Y$
are two monotone determined spaces. Then, a map
![]() $f:CX\rightarrow Y$
is continuous if and only if for each directed subset
$f:CX\rightarrow Y$
is continuous if and only if for each directed subset
![]() ${\mathcal D}\subseteq CX$
and
${\mathcal D}\subseteq CX$
and
![]() $\xi\in CX$
,
$\xi\in CX$
,
![]() ${\mathcal D}\Rightarrow_P\xi$
implies
${\mathcal D}\Rightarrow_P\xi$
implies
![]() $f(\mathcal{D})\rightarrow f(\xi)$
.
$f(\mathcal{D})\rightarrow f(\xi)$
.
Proof. Since
![]() $\Rightarrow_P$
convergence will lead to topological convergence in CX, the necessity is obvious. We need only to prove the sufficiency. First, we check that f is monotone. If
$\Rightarrow_P$
convergence will lead to topological convergence in CX, the necessity is obvious. We need only to prove the sufficiency. First, we check that f is monotone. If
![]() $\xi,\ \eta\in CX$
and
$\xi,\ \eta\in CX$
and
![]() $\xi\leq\eta$
, then
$\xi\leq\eta$
, then
![]() $\{\eta\}\Rightarrow_P\xi$
, by the hypothesis,
$\{\eta\}\Rightarrow_P\xi$
, by the hypothesis,
![]() $\{f(\eta)\}\rightarrow f(\xi)$
, thus
$\{f(\eta)\}\rightarrow f(\xi)$
, thus
![]() $f(\xi)\sqsubseteq f(\eta)$
. Suppose that U is an open subset of Y and the directed set
$f(\xi)\sqsubseteq f(\eta)$
. Suppose that U is an open subset of Y and the directed set
![]() ${\mathcal D}\Rightarrow_P\xi\in f^{-1}(U)$
, then
${\mathcal D}\Rightarrow_P\xi\in f^{-1}(U)$
, then
![]() $f(\mathcal{D})$
is a directed set of Y and
$f(\mathcal{D})$
is a directed set of Y and
![]() $f(\mathcal{D})\rightarrow f(\xi)\in U$
, thus
$f(\mathcal{D})\rightarrow f(\xi)\in U$
, thus
![]() $\exists\ \xi'\in {\mathcal D}$
such that
$\exists\ \xi'\in {\mathcal D}$
such that
![]() $f(\xi')\in U$
. That is,
$f(\xi')\in U$
. That is,
![]() $\xi'\in {\mathcal D}\cap f^{-1}(U)$
. According to the definition of
$\xi'\in {\mathcal D}\cap f^{-1}(U)$
. According to the definition of
![]() $\Rightarrow_P$
convergence open set,
$\Rightarrow_P$
convergence open set,
![]() $f^{-1}(U)\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
, which means that f is continuous.
$f^{-1}(U)\in O_{\Rightarrow_P}(\mathcal{V}_f(X))$
, which means that f is continuous.
The addition operation on CX is defined as follows:
And the scalar multiplication operation on CX is defined as follows:
We now check that the two operations are both continuous, and thus,
![]() $(CX, +, \cdot)$
is a monotone determined cone.
$(CX, +, \cdot)$
is a monotone determined cone.
Theorem 17. Let X be a monotone determined space. Then,
![]() $(CX, +, \cdot)$
is a monotone determined cone.
$(CX, +, \cdot)$
is a monotone determined cone.
Proof. By Proposition 15, CX is a monotone determined space, and by the definition of
![]() $+$
and
$+$
and
![]() $\cdot$
, the two operations are monotone. According to Theorem 2 and Proposition 16, to prove the continuity of
$\cdot$
, the two operations are monotone. According to Theorem 2 and Proposition 16, to prove the continuity of
![]() $+$
, we only need to check that for arbitrary fixed
$+$
, we only need to check that for arbitrary fixed
![]() $\eta=\sum_{j=1}^{m}s_{c_j}\eta_{c_j}\in CX $
(
$\eta=\sum_{j=1}^{m}s_{c_j}\eta_{c_j}\in CX $
(
![]() $c_{j_1}\neq c_{j_2}$
for different
$c_{j_1}\neq c_{j_2}$
for different
![]() $j_1$
and
$j_1$
and
![]() $j_2$
) and a directed set
$j_2$
) and a directed set
![]() $\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$
with
$\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$
with
![]() $\mathcal{D}\Rightarrow_{P}\xi$
, we have
$\mathcal{D}\Rightarrow_{P}\xi$
, we have
![]() $\mathcal{D}+\eta =\{\xi_i +\eta\}_{i\in I}\Rightarrow_{P}\xi +\eta$
. Assume that
$\mathcal{D}+\eta =\{\xi_i +\eta\}_{i\in I}\Rightarrow_{P}\xi +\eta$
. Assume that
![]() $\xi$
has a representation
$\xi$
has a representation
![]() $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
and there exist
$\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
and there exist
![]() $D_1,\cdots,D_n$
– with
$D_1,\cdots,D_n$
– with
![]() $D_i\rightarrow b_i$
for
$D_i\rightarrow b_i$
for
![]() $1\leq i\leq n$
– as in the definition of
$1\leq i\leq n$
– as in the definition of
![]() $\mathcal{D}\Rightarrow_{P}\xi$
.
$\mathcal{D}\Rightarrow_{P}\xi$
.
For an arbitrary
![]() $(d_1,\dots,d_n,c_1,\dots,c_m)\in\prod_{i=1}^{n}D_i\times\prod_{j=1}^{m}\{c_j\}$
, and
$(d_1,\dots,d_n,c_1,\dots,c_m)\in\prod_{i=1}^{n}D_i\times\prod_{j=1}^{m}\{c_j\}$
, and
![]() $\forall r_{b_i}'<r_{b_i},\ s_{c_j}'<s_{c_j},\ i=1,\dots,n,j=1,\dots,m$
, by the definition of
$\forall r_{b_i}'<r_{b_i},\ s_{c_j}'<s_{c_j},\ i=1,\dots,n,j=1,\dots,m$
, by the definition of
![]() $\mathcal{D}\Rightarrow_{P}\xi$
, there exists some
$\mathcal{D}\Rightarrow_{P}\xi$
, there exists some
![]() $\xi'\in\mathcal{D}$
such that
$\xi'\in\mathcal{D}$
such that
![]() $\sum_{i=1}^{n}r_{b_i}'\eta_{d_{i}}\leq\xi'$
. Since
$\sum_{i=1}^{n}r_{b_i}'\eta_{d_{i}}\leq\xi'$
. Since
![]() $+$
is monotone,
$+$
is monotone,
 \[\sum_{i=1}^{n}r_{b_i}'\eta_{d_{i}}+\sum_{j=1}^{m}s_{c_j}'\eta_{c_j}\leq\xi'+\sum_{j=1}^{m}s_{c_j}'\eta_{c_j}\leq \xi'+\eta.\]
\[\sum_{i=1}^{n}r_{b_i}'\eta_{d_{i}}+\sum_{j=1}^{m}s_{c_j}'\eta_{c_j}\leq\xi'+\sum_{j=1}^{m}s_{c_j}'\eta_{c_j}\leq \xi'+\eta.\]
Now, we prove continuity of scalar product. For an arbitrary fixed
![]() $a\in\mathbb{R}^+$
and a directed set
$a\in\mathbb{R}^+$
and a directed set
![]() $\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$
with
$\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$
with
![]() $\mathcal{D}\Rightarrow_{P}\xi$
, we claim that
$\mathcal{D}\Rightarrow_{P}\xi$
, we claim that
![]() $a\cdot\mathcal{D}=\{a\cdot\xi_i\}_{i\in I}\Rightarrow_{P}(a\cdot\xi)$
. By the hypothesis of
$a\cdot\mathcal{D}=\{a\cdot\xi_i\}_{i\in I}\Rightarrow_{P}(a\cdot\xi)$
. By the hypothesis of
![]() $\mathcal{D}\Rightarrow_{P}\xi$
there is a representation of
$\mathcal{D}\Rightarrow_{P}\xi$
there is a representation of
![]() $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
and we have
$\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
and we have
![]() $D_1,\cdots,D_n$
– with
$D_1,\cdots,D_n$
– with
![]() $D_i\rightarrow b_i$
for
$D_i\rightarrow b_i$
for
![]() $1\leq i\leq n$
, for
$1\leq i\leq n$
, for
![]() $\forall\ (d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i,\ \forall\ r_{b_i}'<r_{b_i},i=1,\dots,n$
, there exists
$\forall\ (d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i,\ \forall\ r_{b_i}'<r_{b_i},i=1,\dots,n$
, there exists
![]() $\xi'\in\mathcal{D}$
, such that
$\xi'\in\mathcal{D}$
, such that
![]() $\sum_{i=1}^{n}r_{b_i}'\eta_{d_i}\leq\xi'$
. Hence, we have
$\sum_{i=1}^{n}r_{b_i}'\eta_{d_i}\leq\xi'$
. Hence, we have
![]() $\sum_{i=1}^{n}a\cdot r_{b_i}'\eta_{d_i}\leq a\cdot\xi'$
.
$\sum_{i=1}^{n}a\cdot r_{b_i}'\eta_{d_i}\leq a\cdot\xi'$
.
For arbitrary
![]() $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$
and a directed set
$\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$
and a directed set
![]() $D\subseteq\mathbb{R}^+$
with
$D\subseteq\mathbb{R}^+$
with
![]() $D\rightarrow a$
. We claim that
$D\rightarrow a$
. We claim that
![]() $D\cdot\xi=\{d\cdot\xi\}_{d\in D}\Rightarrow_{P}(a\cdot\xi)$
. Let
$D\cdot\xi=\{d\cdot\xi\}_{d\in D}\Rightarrow_{P}(a\cdot\xi)$
. Let
![]() $D_i=\{b_i\},i=1,\dots,n$
,
$D_i=\{b_i\},i=1,\dots,n$
,
![]() $\forall\ (b_1,\dots,b_n)\in\prod_{i=1}^{n}D_i$
and
$\forall\ (b_1,\dots,b_n)\in\prod_{i=1}^{n}D_i$
and
![]() $\forall\ r_{b_i}'<ar_{b_i},i=1,\dots,n$
, we only need to find
$\forall\ r_{b_i}'<ar_{b_i},i=1,\dots,n$
, we only need to find
![]() $d\in D$
with
$d\in D$
with
![]() $r_{b_i}'\leq dr_{b_i},i=1,\dots,n.$
This is possible, because for each
$r_{b_i}'\leq dr_{b_i},i=1,\dots,n.$
This is possible, because for each
![]() $i=1,\dots,n$
,
$i=1,\dots,n$
,
![]() $\dfrac{r_{b_i}'}{r_{b_i}}<a$
and
$\dfrac{r_{b_i}'}{r_{b_i}}<a$
and
![]() $D\rightarrow a$
.
$D\rightarrow a$
.
In conclusion,
![]() $(CX, +, \cdot)$
is a monotone determined cone.
$(CX, +, \cdot)$
is a monotone determined cone.
We now show that
![]() $(CX, +, \cdot)$
is the free monotone determined cone over X. It is the main result of this section. We begin with one useful lemma.
$(CX, +, \cdot)$
is the free monotone determined cone over X. It is the main result of this section. We begin with one useful lemma.
Proposition 18. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Proposition IV-9.18) (Splitting Lemma) For two simple valuations in
![]() $\mathcal{V}_f(X)$
, where X is a
$\mathcal{V}_f(X)$
, where X is a
![]() $T_0$
space, we have
$T_0$
space, we have
![]() $\zeta=\sum_{b\in B}r_b\eta_b\leq\sum_{c\in C}s_c\eta_c=\xi$
if and only if there exist
$\zeta=\sum_{b\in B}r_b\eta_b\leq\sum_{c\in C}s_c\eta_c=\xi$
if and only if there exist
![]() $\{t_{b,c}\in[0,+\infty):b\in B,\ c\in C\}$
such that for each
$\{t_{b,c}\in[0,+\infty):b\in B,\ c\in C\}$
such that for each
![]() $b\in B,\ c\in C$
,
$b\in B,\ c\in C$
,
and
![]() $t_{b,c}\neq 0$
implies
$t_{b,c}\neq 0$
implies
![]() $b\leq c$
.
$b\leq c$
.
Theorem 19. Let X be a monotone determined space. Then
![]() $(CX, +, \cdot)$
is the monotone determined probabilistic powerspace over X, that is, endowed with topology
$(CX, +, \cdot)$
is the monotone determined probabilistic powerspace over X, that is, endowed with topology
![]() $O_{\Rightarrow_P}(\mathcal{V}_f(X))$
,
$O_{\Rightarrow_P}(\mathcal{V}_f(X))$
,
![]() $(CX, +, \cdot)\cong P_D(X)$
.
$(CX, +, \cdot)\cong P_D(X)$
.
Proof. Define the map
![]() $i:X\rightarrow CX$
as follows:
$i:X\rightarrow CX$
as follows:
![]() $\forall x\in X$
,
$\forall x\in X$
,
![]() $i(x)=\eta_x$
. By Lemma 10, i is injective. We now prove the continuity of i. It is evident that if
$i(x)=\eta_x$
. By Lemma 10, i is injective. We now prove the continuity of i. It is evident that if
![]() $x\leq y\in X$
then
$x\leq y\in X$
then
![]() $\forall U\in\mathcal{O}(X),\ x\in U \Longrightarrow y\in U$
, that is,
$\forall U\in\mathcal{O}(X),\ x\in U \Longrightarrow y\in U$
, that is,
![]() $\eta_x\leq\eta_y$
. Suppose that D is a directed subset of X with
$\eta_x\leq\eta_y$
. Suppose that D is a directed subset of X with
![]() $D \rightarrow x\in X$
. Let
$D \rightarrow x\in X$
. Let
![]() $\mathcal{D}=\{\eta_d:d\in D\}$
, then
$\mathcal{D}=\{\eta_d:d\in D\}$
, then
![]() $i(D)=\mathcal{D}$
is a directed set in CX and
$i(D)=\mathcal{D}$
is a directed set in CX and
![]() ${\mathcal D}\Rightarrow_{P}\eta_x$
. Because, by hypothesis,
${\mathcal D}\Rightarrow_{P}\eta_x$
. Because, by hypothesis,
![]() $D\rightarrow x$
, and
$D\rightarrow x$
, and
![]() $\forall d\in D,\ \forall k<1\ :\ k\eta_d\leq\eta_d$
.
$\forall d\in D,\ \forall k<1\ :\ k\eta_d\leq\eta_d$
.
Let
![]() $(Y, \uplus, \ast)$
be a monotone determined cone and
$(Y, \uplus, \ast)$
be a monotone determined cone and
![]() $f:X\rightarrow Y$
be a continuous map. Define
$f:X\rightarrow Y$
be a continuous map. Define
![]() $\bar{f}:CX\rightarrow Y$
as follows:
$\bar{f}:CX\rightarrow Y$
as follows:
![]() $\forall \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX (\text{supp}(\xi)=\{b_1,\cdots,b_n\})$
,
$\forall \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX (\text{supp}(\xi)=\{b_1,\cdots,b_n\})$
,
By Lemma 10,
![]() $\bar{f}$
is well-defined.
$\bar{f}$
is well-defined.
-
(1)
 $f=\bar{f}\circ i$
.
$f=\bar{f}\circ i$
.
For arbitrary
![]() $x\in X$
,
$x\in X$
,
![]() $(\bar{f}\circ i)(x)=\bar{f}(i(x))=\bar{f}(\eta_x)=f(x)$
.
$(\bar{f}\circ i)(x)=\bar{f}(i(x))=\bar{f}(\eta_x)=f(x)$
.
-
(2)
 $\bar{f}$
is a monotone determined cone homomorphism, that is,
$\bar{f}$
is a monotone determined cone homomorphism, that is,
 $\bar{f}$
is continuous and for arbitrary
$\bar{f}$
is continuous and for arbitrary
 $\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
,
$\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
,
 $\bar{f}(\sum_{i=1}^{n}r_{b_i}\eta_{b_i})=\biguplus_{i=1}^{n}r_{b_i}\ast\bar{f}(\eta_{b_i})$
. This equation is evident since
$\bar{f}(\sum_{i=1}^{n}r_{b_i}\eta_{b_i})=\biguplus_{i=1}^{n}r_{b_i}\ast\bar{f}(\eta_{b_i})$
. This equation is evident since
 $\bar{f}(\eta_{b_i})=f(b_i),\ i=1,\dots,n.$
So, we only need to prove that
$\bar{f}(\eta_{b_i})=f(b_i),\ i=1,\dots,n.$
So, we only need to prove that
 $\bar{f}$
is continuous.
$\bar{f}$
is continuous.
First,
![]() $\bar{f}$
is monotone. Let
$\bar{f}$
is monotone. Let
![]() $\zeta=\sum_{b\in B}r_b\eta_b\leq\sum_{c\in C}s_c\eta_c=\xi$
. By Proposition 18, there exist
$\zeta=\sum_{b\in B}r_b\eta_b\leq\sum_{c\in C}s_c\eta_c=\xi$
. By Proposition 18, there exist
![]() $\{t_{b,c}\in[0,+\infty):b\in B,\ c\in C\}$
such that for each
$\{t_{b,c}\in[0,+\infty):b\in B,\ c\in C\}$
such that for each
![]() $b\in B,\ c\in C$
,
$b\in B,\ c\in C$
,
and
![]() $t_{b,c}\neq 0$
implies
$t_{b,c}\neq 0$
implies
![]() $b\leq c$
. From the definition of
$b\leq c$
. From the definition of
![]() $\bar{f,}$
we have
$\bar{f,}$
we have
By Proposition 16, to show the continuity of
![]() $\overline{f}$
, we need only to prove that
$\overline{f}$
, we need only to prove that
![]() $\bar{f}$
preserves
$\bar{f}$
preserves
![]() $\Rightarrow_{P}$
convergence class. Suppose that we have a directed set
$\Rightarrow_{P}$
convergence class. Suppose that we have a directed set
![]() $\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$
and
$\mathcal{D}=\{\xi_i\}_{i\in I}\subseteq CX$
and
![]() $\xi\in CX$
with
$\xi\in CX$
with
![]() $\mathcal{D}\Rightarrow_{P}\xi$
, then, we need to show that
$\mathcal{D}\Rightarrow_{P}\xi$
, then, we need to show that
![]() $\bar{f}(\mathcal{D})\rightarrow\bar{f}(\xi)$
in Y. There is a representation
$\bar{f}(\mathcal{D})\rightarrow\bar{f}(\xi)$
in Y. There is a representation
![]() $\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
and let
$\xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}$
and let
![]() $D_1,\cdots,D_n$
with
$D_1,\cdots,D_n$
with
![]() $D_i\rightarrow b_i (1\leq i\leq n)$
be as in the definition of
$D_i\rightarrow b_i (1\leq i\leq n)$
be as in the definition of
![]() $\mathcal{D}\Rightarrow_{P}\xi$
. From the continuity of
$\mathcal{D}\Rightarrow_{P}\xi$
. From the continuity of
![]() $f,\ \uplus$
and
$f,\ \uplus$
and
![]() $\ast$
, we have
$\ast$
, we have
Notice that
![]() $\mathcal{E}=\{(r_{b_1}'\ast f(d_1))\uplus\dots\uplus (r_{b_n}'\ast f(d_n)):(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i, r_{b_i}'<r_{b_i},i=1,\cdots,n\}$
is a directed set in Y. For an arbitrary open neighborhood U of
$\mathcal{E}=\{(r_{b_1}'\ast f(d_1))\uplus\dots\uplus (r_{b_n}'\ast f(d_n)):(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i, r_{b_i}'<r_{b_i},i=1,\cdots,n\}$
is a directed set in Y. For an arbitrary open neighborhood U of
![]() $\bar{f}(\xi)$
, there exists some
$\bar{f}(\xi)$
, there exists some
![]() $(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$
and
$(d_1,\dots,d_n)\in\prod_{i=1}^{n}D_i$
and
![]() $r_{b_i}'<r_{b_i},i=1,\cdots,n$
such that
$r_{b_i}'<r_{b_i},i=1,\cdots,n$
such that
![]() $\biguplus_{i=1}^{n}r_{b_i}'\ast f(d_i)\in U$
. For the given
$\biguplus_{i=1}^{n}r_{b_i}'\ast f(d_i)\in U$
. For the given
![]() $d_1,\dots,d_n$
and
$d_1,\dots,d_n$
and
![]() $r_{b_i}'<r_{b_i},i=1,\dots,n$
, again by the definition of
$r_{b_i}'<r_{b_i},i=1,\dots,n$
, again by the definition of
![]() $\mathcal{D}\Rightarrow_{P}\xi$
, there exists some
$\mathcal{D}\Rightarrow_{P}\xi$
, there exists some
![]() $\xi'\in\mathcal{D}$
such that
$\xi'\in\mathcal{D}$
such that
![]() $\sum_{i=1}^{n}r_{b_i}'\eta_{d_i}\leq\xi'$
. Then
$\sum_{i=1}^{n}r_{b_i}'\eta_{d_i}\leq\xi'$
. Then
![]() $\bar{f}(\sum_{i=1}^{n}r_{b_i}'\eta_{d_i})=\biguplus_{i=1}^{n}r_{b_i}'\ast f(d_i)\leq\bar{f}(\xi')$
. Since U is an upper set, then
$\bar{f}(\sum_{i=1}^{n}r_{b_i}'\eta_{d_i})=\biguplus_{i=1}^{n}r_{b_i}'\ast f(d_i)\leq\bar{f}(\xi')$
. Since U is an upper set, then
![]() $\bar{f}(\xi')$
is included in U. Hence,
$\bar{f}(\xi')$
is included in U. Hence,
![]() $\bar{f}$
is continuous.
$\bar{f}$
is continuous.
-
(3) The homomorphism
 $\bar{f}$
is unique.
$\bar{f}$
is unique.
Suppose we have a monotone determined cone homomorphism
![]() $g:(CX, +, \cdot)\rightarrow (Y, \uplus, \ast)$
such that
$g:(CX, +, \cdot)\rightarrow (Y, \uplus, \ast)$
such that
![]() $f=g\circ i$
, then
$f=g\circ i$
, then
![]() $g(\eta_x)=f(x)=\bar{f}(\eta_x)$
. For each
$g(\eta_x)=f(x)=\bar{f}(\eta_x)$
. For each
![]() $ \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$
,
$ \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$
,
 \begin{eqnarray*} g(\xi)&=& g(r_{b_1}\eta_{b_1}+r_{b_2}\eta_{b_2}\cdots+r_{b_n}\eta_{b_n})\\ &=&g(r_{b_1}\eta_{b_1})\uplus g(r_{b_2}\eta_{b_2})\uplus \cdots \uplus g(r_{b_n}\eta_{b_n})\\ &=&r_{b_1}\ast g(\eta_{b_1})\uplus r_{b_2}\ast g(\eta_{b_2})\uplus \cdots\uplus r_{b_n}\ast g( \eta_{b_n})\\ &=&r_{b_1}\ast f({b_1})\uplus r_{b_2}\ast f({b_2})\uplus \cdots\uplus r_{b_n}\ast f({b_n})\\ &=&\bar{f}(\xi). \end{eqnarray*}
\begin{eqnarray*} g(\xi)&=& g(r_{b_1}\eta_{b_1}+r_{b_2}\eta_{b_2}\cdots+r_{b_n}\eta_{b_n})\\ &=&g(r_{b_1}\eta_{b_1})\uplus g(r_{b_2}\eta_{b_2})\uplus \cdots \uplus g(r_{b_n}\eta_{b_n})\\ &=&r_{b_1}\ast g(\eta_{b_1})\uplus r_{b_2}\ast g(\eta_{b_2})\uplus \cdots\uplus r_{b_n}\ast g( \eta_{b_n})\\ &=&r_{b_1}\ast f({b_1})\uplus r_{b_2}\ast f({b_2})\uplus \cdots\uplus r_{b_n}\ast f({b_n})\\ &=&\bar{f}(\xi). \end{eqnarray*}
Thus
![]() $\bar{f}$
is unique.
$\bar{f}$
is unique.
In conclusion, the monotone determined cone
![]() $(CX, +, \cdot)$
is the monotone determined probabilistic powerspace of X, that is,
$(CX, +, \cdot)$
is the monotone determined probabilistic powerspace of X, that is,
![]() $P_D(X)\cong (CX, +, \cdot)$
.
$P_D(X)\cong (CX, +, \cdot)$
.
Remark 20. A related result is from Heckmann. It was shown that
![]() $\mathcal{V}_f(X)$
with weak topology is the free locally convex
$\mathcal{V}_f(X)$
with weak topology is the free locally convex
![]() $T_0$
cone over X in TOP (Heckmann Reference Heckmann, Andima, Flagg, Itzkowitz, Misra, Kong and Kopperman1996, Theorem 7.6). The difference between our results is that the two topologies on
$T_0$
cone over X in TOP (Heckmann Reference Heckmann, Andima, Flagg, Itzkowitz, Misra, Kong and Kopperman1996, Theorem 7.6). The difference between our results is that the two topologies on
![]() $\mathcal{V}_f(X)$
are not the same generally.
$\mathcal{V}_f(X)$
are not the same generally.
The monotone determined probabilistic powerspace is unique up to algebraic isomorphism and topological homemorphism, so we can directly denote the monotone determined probabilistic powerspace by
![]() $P_D(X)=(CX, +, \cdot)$
for each monotone determined space X.
$P_D(X)=(CX, +, \cdot)$
for each monotone determined space X.
Suppose that X and Y are two monotone determined spaces and
![]() $f:X\rightarrow Y$
is a continuous map. Define the map
$f:X\rightarrow Y$
is a continuous map. Define the map
![]() $P_D(f):P_D(X)\rightarrow P_D(Y)$
as follows:
$P_D(f):P_D(X)\rightarrow P_D(Y)$
as follows:
![]() $\forall \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$
,
$\forall \xi=\sum_{i=1}^{n}r_{b_i}\eta_{b_i}\in CX$
,
![]() $P_D(f)$
is well-defined and order preserving. It is also easy to check that,
$P_D(f)$
is well-defined and order preserving. It is also easy to check that,
![]() $P_D(f)$
is a monotone determined cone homomorphism between these two extended probabilistic powerspaces. If
$P_D(f)$
is a monotone determined cone homomorphism between these two extended probabilistic powerspaces. If
![]() $id_X$
is the identity map and
$id_X$
is the identity map and
![]() $g:Y\rightarrow Z$
is an arbitrary continuous map from Y to a monotone determined space Z, then,
$g:Y\rightarrow Z$
is an arbitrary continuous map from Y to a monotone determined space Z, then,
![]() $P_D(id_X)=id_{P_D(X)},\ P_D(g\circ f)=P_D(g)\circ P_D(f)$
. Thus,
$P_D(id_X)=id_{P_D(X)},\ P_D(g\circ f)=P_D(g)\circ P_D(f)$
. Thus,
![]() $P_D:{\bf Dtop}\rightarrow {\bf Dscone}$
is a functor from Dtop to Dscone. Let
$P_D:{\bf Dtop}\rightarrow {\bf Dscone}$
is a functor from Dtop to Dscone. Let
![]() $U:{\bf Dscone}\rightarrow {\bf Dtop}$
be the forgetful functor. By Theorem 19, we have the following result.
$U:{\bf Dscone}\rightarrow {\bf Dtop}$
be the forgetful functor. By Theorem 19, we have the following result.
Corollary 21.
![]() $P_D$
is the left adjoint of the forgetful functor U, that is, Dscone is a reflective subcategory of Dtop.
$P_D$
is the left adjoint of the forgetful functor U, that is, Dscone is a reflective subcategory of Dtop.
Remark 22. Let X be a c-space, is
![]() $P_D(X)$
still a c-space? We will answer this question in the last section of this paper.
$P_D(X)$
still a c-space? We will answer this question in the last section of this paper.
4. D-Completion and Free dcpo-cone over Any dcpo
Monotone convergence spaces (a.k.a d-spaces) form a very important class of
![]() $T_0$
topological spaces in domain theory. Interestingly, every
$T_0$
topological spaces in domain theory. Interestingly, every
![]() $T_0$
space has a D-completion (See Definition 25). In this section, we will recall some notions about D-completions which are useful for our further discussions.
$T_0$
space has a D-completion (See Definition 25). In this section, we will recall some notions about D-completions which are useful for our further discussions.
Definition 23. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003,Definition II-3.12) Let X be a
![]() $T_0$
space. If X with the specialization order
$T_0$
space. If X with the specialization order
![]() $(X,\leq)$
is a dcpo and every open set of X is Scott open in
$(X,\leq)$
is a dcpo and every open set of X is Scott open in
![]() $(X,\leq)$
, then we call X a monotone convergence space.
$(X,\leq)$
, then we call X a monotone convergence space.
A subset A of a poset P is called d-closed if for every directed subset D of A that possesses supremum
![]() $\bigvee D$
,
$\bigvee D$
,
![]() $\bigvee D$
is included in A. The d-closed sets form the closed sets for a topology, called the d-topology (Keimel and Lawson Reference Keimel and Lawson2009, Lemma 5.1). We denote the closure of A in P with d-topology by
$\bigvee D$
is included in A. The d-closed sets form the closed sets for a topology, called the d-topology (Keimel and Lawson Reference Keimel and Lawson2009, Lemma 5.1). We denote the closure of A in P with d-topology by
![]() $\text{cl}_{d}(A)$
. If
$\text{cl}_{d}(A)$
. If
![]() $\text{cl}_{d}(A)$
is equal to P, then we say that A is d-dense in P. A map f from a poset P to a poset Q is called d-continuous if f is continuous under the d-topology.
$\text{cl}_{d}(A)$
is equal to P, then we say that A is d-dense in P. A map f from a poset P to a poset Q is called d-continuous if f is continuous under the d-topology.
Lemma 24. (Keimel and Lawson Reference Keimel and Lawson2009, Lemma 6.3) Consider the following properties for a subset A of a
![]() $T_0$
space X
$T_0$
space X
-
(1) A is a monotone convergence space.
-
(2) A is a sub-dcpo.
-
(3) A is d-closed.
Then, (1) implies (2) and (2) implies (3), and all three are equivalent if X is a monotone convergence space.
Definition 25. (Keimel and Lawson Reference Keimel and Lawson2009, Definition 6.5) An embedding
![]() $j\colon X\rightarrow\tilde{X}$
of a space X with image a d-dense subset of a monotone convergence space
$j\colon X\rightarrow\tilde{X}$
of a space X with image a d-dense subset of a monotone convergence space
![]() $\tilde{X}$
is called a D-completion.
$\tilde{X}$
is called a D-completion.
The following result says that D-completions are universal, and hence, they are unique up to isomorphism.
Theorem . (Keimel and Lawson Reference Keimel and Lawson2009, Theorem 6.7) Let
![]() $j\colon X\rightarrow Y$
be a topological embedding of a space X into a monotone convergence space Y. Let
$j\colon X\rightarrow Y$
be a topological embedding of a space X into a monotone convergence space Y. Let
![]() $\tilde{X}=\text{cl}_{d}(j(X))$
be the d-closure of j(X) in Y, equipped with the relative topology from Y. Then
$\tilde{X}=\text{cl}_{d}(j(X))$
be the d-closure of j(X) in Y, equipped with the relative topology from Y. Then
![]() $k\colon X\rightarrow \tilde{X}$
, the co-restriction of j, is a universal D-completion, that is, for every continuous map f from X to a monotone convergence space M, there is a unique continuous map
$k\colon X\rightarrow \tilde{X}$
, the co-restriction of j, is a universal D-completion, that is, for every continuous map f from X to a monotone convergence space M, there is a unique continuous map
![]() $\tilde{f}\colon\tilde{X}\rightarrow M$
such that
$\tilde{f}\colon\tilde{X}\rightarrow M$
such that
![]() $\tilde{f}\circ k=f$
.
$\tilde{f}\circ k=f$
.
Proposition 26. Let X be a
![]() $T_0$
space and
$T_0$
space and
![]() $X^{d}$
be its D-completion. Then,
$X^{d}$
be its D-completion. Then,
![]() $\mathcal{O}(X)\cong \mathcal{O}(X^{d})$
.
$\mathcal{O}(X)\cong \mathcal{O}(X^{d})$
.
Proof. Let
![]() $f\colon X\rightarrow X^{s}$
be the soberification map. Since
$f\colon X\rightarrow X^{s}$
be the soberification map. Since
![]() $X^{s}$
is sober, it is a monotone convergence space (Goubault-Larrecq Reference Goubault-Larrecq2013, Proposition 8.2.34), the D-completion
$X^{s}$
is sober, it is a monotone convergence space (Goubault-Larrecq Reference Goubault-Larrecq2013, Proposition 8.2.34), the D-completion
![]() $X^{d}$
of X can be regarded as a subspace of
$X^{d}$
of X can be regarded as a subspace of
![]() $X^{s}$
by Theorem 4. Then,
$X^{s}$
by Theorem 4. Then,
![]() $X^{s}$
is also a soberification of
$X^{s}$
is also a soberification of
![]() $X^{d}$
. We conclude that
$X^{d}$
. We conclude that
![]() $\mathcal{O}(X)\cong \mathcal{O}(X^{d})$
directly.
$\mathcal{O}(X)\cong \mathcal{O}(X^{d})$
directly.
Next we introduce the concept of Scott completion.
Definition 27. (Zhang et al. Reference Zhang, Shi and Li2022, Definition 4.4) A Scott completion (Y, f) of a space X is a Scott space Y together with a continuous map
![]() $f\colon X\rightarrow Y$
such that for any Scott space Z and continuous map
$f\colon X\rightarrow Y$
such that for any Scott space Z and continuous map
![]() $g\colon X\rightarrow Z$
, there exists a unique continuous map
$g\colon X\rightarrow Z$
, there exists a unique continuous map
![]() $\tilde{g}$
satisfying
$\tilde{g}$
satisfying
![]() $g =\tilde{g}\circ f$
.
$g =\tilde{g}\circ f$
.
Not every space has a Scott completion (see the following Example 28). An alternative argument is that the category of Scott space with continuous maps is not reflective in the category of
![]() $T_0$
spaces, we refer to Sheng et al. (Reference Sheng, Xi and Zhao2023, Theorem 3.6).
$T_0$
spaces, we refer to Sheng et al. (Reference Sheng, Xi and Zhao2023, Theorem 3.6).
Example 28 Let
![]() $\mathbb{N}$
be the set of natural numbers endowed with co-finite topology.
$\mathbb{N}$
be the set of natural numbers endowed with co-finite topology.
Claim:
![]() $\mathbb{N}$
does not have a Scott completion. To obtain a contradiction, assume that
$\mathbb{N}$
does not have a Scott completion. To obtain a contradiction, assume that
![]() $\mathbb{N}$
has a Scott completion
$\mathbb{N}$
has a Scott completion
![]() $(\bar{\mathbb{N}},f)$
, where f is a continuous map from
$(\bar{\mathbb{N}},f)$
, where f is a continuous map from
![]() $\mathbb{N}$
to the Scott space
$\mathbb{N}$
to the Scott space
![]() $\bar{\mathbb{N}}$
.
$\bar{\mathbb{N}}$
.
(1) f is injective.
For any two different numbers n and m, consider the Sierpinski space
![]() $\mathbb{S}$
which is the poset
$\mathbb{S}$
which is the poset
![]() $\{\bot,\top\} (\bot<\top)$
equipped with its Scott topology. Define a continuous map
$\{\bot,\top\} (\bot<\top)$
equipped with its Scott topology. Define a continuous map
![]() $g\colon\mathbb{N}\rightarrow\mathbb{S}$
as follows:
$g\colon\mathbb{N}\rightarrow\mathbb{S}$
as follows:
![]() $g(n)=\bot, g(x)=\top $
for any
$g(n)=\bot, g(x)=\top $
for any
![]() $x\neq n$
. Since
$x\neq n$
. Since
![]() $(\bar{\mathbb{N}},f)$
is a Scott completion, there is a continuous map
$(\bar{\mathbb{N}},f)$
is a Scott completion, there is a continuous map
![]() $\tilde{g}\colon\bar{\mathbb{N}}\rightarrow\mathbb{S}$
such that
$\tilde{g}\colon\bar{\mathbb{N}}\rightarrow\mathbb{S}$
such that
![]() $\tilde{g}\circ f=g$
. It follows that
$\tilde{g}\circ f=g$
. It follows that
![]() $\tilde{g}(f(n))=g(n)=\bot, \tilde{g}(f(m))=g(m)=\top$
. Hence,
$\tilde{g}(f(n))=g(n)=\bot, \tilde{g}(f(m))=g(m)=\top$
. Hence,
![]() $f(n)\neq f(m)$
.
$f(n)\neq f(m)$
.
(2) For any two different numbers n,m of
 $\mathbb{N}$
, f(n) and f(m) are incomparable in
$\mathbb{N}$
, f(n) and f(m) are incomparable in
 $\bar{\mathbb{N}}$
.
$\bar{\mathbb{N}}$
.
Without loss of generality, we assume that
![]() $f(m)<f(n)$
. By the same argument of the first step,
$f(m)<f(n)$
. By the same argument of the first step,
![]() $\top=g(m)=\tilde{g}(f(m))\leq\tilde{g}(f(n))=g(n)=\bot$
, a contradiction.
$\top=g(m)=\tilde{g}(f(m))\leq\tilde{g}(f(n))=g(n)=\bot$
, a contradiction.
(3) For any
 $x\in\bar{\mathbb{N}}, $
there is some
$x\in\bar{\mathbb{N}}, $
there is some
 $n\in\mathbb{N}$
such that
$n\in\mathbb{N}$
such that
 $f(n)\leq x$
. In other words,
$f(n)\leq x$
. In other words,
 ${\downarrow}x\cap f(\mathbb{N})\neq\emptyset$
. To obtain a contradiction, suppose there is some
${\downarrow}x\cap f(\mathbb{N})\neq\emptyset$
. To obtain a contradiction, suppose there is some
 $x_0\in\bar{\mathbb{N}}$
with
$x_0\in\bar{\mathbb{N}}$
with
 ${\downarrow}x_0\cap f(\mathbb{N})=\emptyset$
. We take a constant map
${\downarrow}x_0\cap f(\mathbb{N})=\emptyset$
. We take a constant map
 $g=\lambda n.\top\colon\mathbb{N}\rightarrow\mathbb{S}$
. Clearly, it is continuous. Now let us consider two continuous maps
$g=\lambda n.\top\colon\mathbb{N}\rightarrow\mathbb{S}$
. Clearly, it is continuous. Now let us consider two continuous maps
 $g_1, g_2\colon\bar{\mathbb{N}}\rightarrow\mathbb{S}$
as follows:
$g_1, g_2\colon\bar{\mathbb{N}}\rightarrow\mathbb{S}$
as follows:  \[g_1(x)=\top,\forall x;\]
\[g_1(x)=\top,\forall x;\]
 \[g_2(x)= \begin{cases} \top, & x\not\leq x_0,\\ \bot, & x \leq x_0. \end{cases}\]
\[g_2(x)= \begin{cases} \top, & x\not\leq x_0,\\ \bot, & x \leq x_0. \end{cases}\]
It is easy to verify that
![]() $g=g_1\circ f=g_2\circ f$
, which contradicts the uniqueness of
$g=g_1\circ f=g_2\circ f$
, which contradicts the uniqueness of
![]() $\tilde{g}$
.
$\tilde{g}$
.
We conclude that
![]() $f(\mathbb{N})$
is the set of minimal elements of
$f(\mathbb{N})$
is the set of minimal elements of
![]() $\bar{\mathbb{N}}$
from (1), (2) and (3). Notice that every subset A of
$\bar{\mathbb{N}}$
from (1), (2) and (3). Notice that every subset A of
![]() $f(\mathbb{N})$
is Scott closed in
$f(\mathbb{N})$
is Scott closed in
![]() $\bar{\mathbb{N}}$
. Hence,
$\bar{\mathbb{N}}$
. Hence,
![]() $f(\mathbb{N})$
with its subspace topology of
$f(\mathbb{N})$
with its subspace topology of
![]() $\bar{\mathbb{N}}$
is a discrete space. It follows that
$\bar{\mathbb{N}}$
is a discrete space. It follows that
![]() $f^{-1}(A)$
is closed in
$f^{-1}(A)$
is closed in
![]() $\mathbb{N}$
for any
$\mathbb{N}$
for any
![]() $A\subseteq f(X)$
. We see at once that
$A\subseteq f(X)$
. We see at once that
![]() $\mathbb{N}$
is a discrete space as well, a contradiction.
$\mathbb{N}$
is a discrete space as well, a contradiction.
But any poset with Scott topology has a Scott completion (Keimel and Lawson Reference Keimel and Lawson2009) and the following result tells us that every monotone determined space has a Scott completion. Let X be a monotone determined space. The map
![]() $i\colon X\rightarrow \Gamma X$
is defined by
$i\colon X\rightarrow \Gamma X$
is defined by
![]() $i(x)={\downarrow}x$
, where
$i(x)={\downarrow}x$
, where
![]() $\Gamma X$
is the lattice of closed subsets of X. We denote the d-closure of
$\Gamma X$
is the lattice of closed subsets of X. We denote the d-closure of
![]() $i(X)=\{{\downarrow}x:x\in X\}$
in
$i(X)=\{{\downarrow}x:x\in X\}$
in
![]() $\Gamma X$
by
$\Gamma X$
by
![]() $\tilde{X}$
. The map
$\tilde{X}$
. The map
![]() $i\colon X\rightarrow\tilde{X}$
has the universal property: For any Scott space Z and any continuous map
$i\colon X\rightarrow\tilde{X}$
has the universal property: For any Scott space Z and any continuous map
![]() $f\colon X\rightarrow Z$
, there is a unique Scott continuous map
$f\colon X\rightarrow Z$
, there is a unique Scott continuous map
![]() $\bar{f}\colon\tilde{X}\rightarrow Z$
which is defined by
$\bar{f}\colon\tilde{X}\rightarrow Z$
which is defined by
![]() $\bar{f}(A)=\bigvee\text{cl}_{\sigma}(f(A))$
, such that
$\bar{f}(A)=\bigvee\text{cl}_{\sigma}(f(A))$
, such that
![]() $f=\bar{f}\circ i$
.
$f=\bar{f}\circ i$
.
Theorem 29. (Zhang et al. Reference Zhang, Shi and Li2022, Theorem 4.7) Let X be a monotone determined space. Then,
![]() $(\tilde{X},i)$
is a Scott completion of X, which we call the standard Scott completion.
$(\tilde{X},i)$
is a Scott completion of X, which we call the standard Scott completion.
Remark 30. Let X be a monotone determined space. The Scott completion of X is just the D-completion of X because the D-completion of X is a Scott space. An interesting question is: the D-completions of which kind of
![]() $T_0$
spaces are Scott spaces.
$T_0$
spaces are Scott spaces.
Next, we will recall some basic properties of dcpo-cones. As far as we know, there is no representation of free dcpo-cone over general dcpos. In this section, we will construct the free dcpo-cone over any dcpo by using the Scott completion of a monotone determined space.
Definition 31. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Definition IV-9.20) A dcpo-cone is a dcpo C equipped with a distinguished element
![]() $0\in C$
, an addition
$0\in C$
, an addition
![]() $+:C\times C\rightarrow C$
which is Scott continuous, and a scalar multiplication
$+:C\times C\rightarrow C$
which is Scott continuous, and a scalar multiplication
![]() $\cdot:\mathbb{R}^{+}\times C\rightarrow C$
which is Scott continuous, such that the usual axioms of a vector space hold, except for the existence of an additive inverse (in this case, one also assumes that
$\cdot:\mathbb{R}^{+}\times C\rightarrow C$
which is Scott continuous, such that the usual axioms of a vector space hold, except for the existence of an additive inverse (in this case, one also assumes that
![]() $0\cdot a=0$
for any
$0\cdot a=0$
for any
![]() $a\in C$
.)
$a\in C$
.)
Definition 32. Let C,D be two dcpo-cones. A map
![]() $f\colon C\rightarrow D$
is said to be linear if
$f\colon C\rightarrow D$
is said to be linear if
and
Let Dcone denote the category of dcpo-cones with Scott continuous linear maps.
Lemma 33. (Keimel and Lawson Reference Keimel and Lawson2012, Lemma 3.4) Let
![]() $f\colon\prod_{i=1}^{n}X_i\rightarrow Y$
be separately continuous. Then for arbitrary nonempty subsets,
$f\colon\prod_{i=1}^{n}X_i\rightarrow Y$
be separately continuous. Then for arbitrary nonempty subsets,
![]() $A_i\subseteq X_i$
for
$A_i\subseteq X_i$
for
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $B\subseteq Y:$
$B\subseteq Y:$
-
(1)
 $f(\prod_{i=1}^{n}\bar{A_i})\subseteq\bar{B}$
whenever
$f(\prod_{i=1}^{n}\bar{A_i})\subseteq\bar{B}$
whenever
 $f(\prod_{i=1}^{n}A_i)\subseteq B$
;
$f(\prod_{i=1}^{n}A_i)\subseteq B$
; -
(2)
 $\overline{f(\prod_{i=1}^{n}\bar{A_i})}=\overline{f(\prod_{i=1}^{n}A_i)}$
;
$\overline{f(\prod_{i=1}^{n}\bar{A_i})}=\overline{f(\prod_{i=1}^{n}A_i)}$
; -
(3)
 $f^{\gamma}\colon\prod_{i=1}^{n}\Gamma X_i\rightarrow\Gamma Y$
is separately continuous, hence Scott continuous. Here the definition of
$f^{\gamma}\colon\prod_{i=1}^{n}\Gamma X_i\rightarrow\Gamma Y$
is separately continuous, hence Scott continuous. Here the definition of
 $f^{\gamma}$
is as follows:
$f^{\gamma}$
is as follows:  \[f^{\gamma}(A_1,\cdots,A_n)=\overline{f\left(\prod_{i=1}^{n}A_i\right)}=\overline{\{f(x_1,\cdots,x_n):x_i\in A_i \text{for} 1\leq i\leq n\}}.\]
\[f^{\gamma}(A_1,\cdots,A_n)=\overline{f\left(\prod_{i=1}^{n}A_i\right)}=\overline{\{f(x_1,\cdots,x_n):x_i\in A_i \text{for} 1\leq i\leq n\}}.\]
Definition 34. Let X be a monotone determined cone. We denote the Scott completion of X by
![]() $\tilde{X}$
. For any
$\tilde{X}$
. For any
![]() $A,B\in \Gamma X$
, we define
$A,B\in \Gamma X$
, we define
![]() $A\oplus B=\text{cl}\{a+b:a\in A,b\in B\}$
,
$A\oplus B=\text{cl}\{a+b:a\in A,b\in B\}$
,
![]() $r\odot A=\{ra:a\in A\}$
for all
$r\odot A=\{ra:a\in A\}$
for all
![]() $r\in\mathbb{R^+}$
.
$r\in\mathbb{R^+}$
.
Next we will verify that
![]() $\tilde{X}$
with these two operations is a dcpo-cone.
$\tilde{X}$
with these two operations is a dcpo-cone.
Lemma 35. Let X be a monotone determined cone. The Scott completion
![]() $(\tilde{X},\oplus,\odot)$
is a dcpo-cone.
$(\tilde{X},\oplus,\odot)$
is a dcpo-cone.
Proof. It is easy to see that
![]() $X\rightarrow\tilde{X}$
is a linear map. First, we show that
$X\rightarrow\tilde{X}$
is a linear map. First, we show that
![]() $\oplus\colon\tilde{X}\times\tilde{X}\rightarrow\tilde{X}$
is a well-defined Scott continuous map. By Lemma 33(3),
$\oplus\colon\tilde{X}\times\tilde{X}\rightarrow\tilde{X}$
is a well-defined Scott continuous map. By Lemma 33(3),
![]() $\oplus\colon\Gamma X\times\Gamma X\rightarrow\Gamma X$
is Scott continuous, hence d-continuous. For any
$\oplus\colon\Gamma X\times\Gamma X\rightarrow\Gamma X$
is Scott continuous, hence d-continuous. For any
![]() $A \in\tilde{X}$
, we consider a map
$A \in\tilde{X}$
, we consider a map
![]() $g\colon\Gamma X\rightarrow\Gamma X, g(F)=A\oplus F, \forall F\in\Gamma X$
. Since g is d-continuous,
$g\colon\Gamma X\rightarrow\Gamma X, g(F)=A\oplus F, \forall F\in\Gamma X$
. Since g is d-continuous,
Next we consider another map
![]() $h\colon\Gamma X\rightarrow\Gamma X, h(F)=F\oplus{\downarrow}y$
for a given
$h\colon\Gamma X\rightarrow\Gamma X, h(F)=F\oplus{\downarrow}y$
for a given
![]() $y\in X$
.
$y\in X$
.

Hence, we obtain that
![]() $A\oplus B\in\tilde{X}$
.
$A\oplus B\in\tilde{X}$
.
Second for any
![]() $A,B,C\in\Gamma X$
, obviously
$A,B,C\in\Gamma X$
, obviously
![]() $A\oplus B=B\oplus A$
,
$A\oplus B=B\oplus A$
,
![]() $A\oplus {\downarrow}0=A$
, and:
$A\oplus {\downarrow}0=A$
, and:
 \begin{align*}\overline{\{a+b+c:a\in A,b\in B,c\in C\}}&\subseteq A\oplus(B\oplus C)\\ &=\overline{\{a+x:a\in A,x\in B\oplus C\}}\\ &=\overline{\bigcup_{a\in A}\{a+x:x\in B\oplus C\}}\\ &\subseteq\overline{\bigcup_{a\in A}cl\{a+(b+c):b\in B,c\in C\}} (\lambda x.a+x\colon X\rightarrow X \text{is continuous})\\ &\subseteq \overline{\{a+b+c:a\in A,b\in B,c\in C\}}\end{align*}
\begin{align*}\overline{\{a+b+c:a\in A,b\in B,c\in C\}}&\subseteq A\oplus(B\oplus C)\\ &=\overline{\{a+x:a\in A,x\in B\oplus C\}}\\ &=\overline{\bigcup_{a\in A}\{a+x:x\in B\oplus C\}}\\ &\subseteq\overline{\bigcup_{a\in A}cl\{a+(b+c):b\in B,c\in C\}} (\lambda x.a+x\colon X\rightarrow X \text{is continuous})\\ &\subseteq \overline{\{a+b+c:a\in A,b\in B,c\in C\}}\end{align*}
Thus, we have
![]() $A\oplus (B\oplus C)=\overline{\{a+b+c:a\in A,b\in B,c\in C\}}$
. For the same reason,
$A\oplus (B\oplus C)=\overline{\{a+b+c:a\in A,b\in B,c\in C\}}$
. For the same reason,
![]() $(A\oplus B)\oplus C$
is equal to
$(A\oplus B)\oplus C$
is equal to
![]() $\overline{\{a+b+c:a\in A,b\in B,c\in C\}}$
. Therefore,
$\overline{\{a+b+c:a\in A,b\in B,c\in C\}}$
. Therefore,
![]() $(A\oplus B)\oplus C=A\oplus (B\oplus C)$
.
$(A\oplus B)\oplus C=A\oplus (B\oplus C)$
.
For any positive real number r, the map
![]() $\lambda x.rx\colon X\rightarrow X$
is a homomorphism. Hence,
$\lambda x.rx\colon X\rightarrow X$
is a homomorphism. Hence,
![]() $r\odot F=\{ra:a\in F\}\in\Gamma X$
for each
$r\odot F=\{ra:a\in F\}\in\Gamma X$
for each
![]() $F\in\Gamma X$
. Note that the map
$F\in\Gamma X$
. Note that the map
![]() $f=\lambda F.r\odot F\colon\Gamma X\rightarrow\Gamma X$
is an order isomorphism under the inclusion ordering. For any
$f=\lambda F.r\odot F\colon\Gamma X\rightarrow\Gamma X$
is an order isomorphism under the inclusion ordering. For any
![]() $A\in\tilde{X}$
,
$A\in\tilde{X}$
,

Therefore, the map
![]() $\lambda A.r\odot A\colon\tilde{X}\rightarrow\tilde{X}$
is well-defined and Scott continuous.
$\lambda A.r\odot A\colon\tilde{X}\rightarrow\tilde{X}$
is well-defined and Scott continuous.
Given any non-negative real numbers r,s and
![]() $A,B\in\tilde{X}$
,learly
$A,B\in\tilde{X}$
,learly
and
Next we show that
If
![]() $A={\downarrow}x$
for some
$A={\downarrow}x$
for some
![]() $x\in X$
, then
$x\in X$
, then
![]() $(r+s)\odot{\downarrow}x={\downarrow}(r+s)x$
and
$(r+s)\odot{\downarrow}x={\downarrow}(r+s)x$
and
![]() $(r\odot{\downarrow}x)\oplus (s\odot{\downarrow}x)$
=
$(r\odot{\downarrow}x)\oplus (s\odot{\downarrow}x)$
=
![]() $\overline{\{ra+sb:a\leq x,b\leq x\}}={\downarrow}(r+s)x$
. We set
$\overline{\{ra+sb:a\leq x,b\leq x\}}={\downarrow}(r+s)x$
. We set
![]() $\mathcal{S}:=\{C\in\Gamma X:(r+s)\odot C=(r\odot C)\oplus (s\odot C)\}$
. By the preceding argument,
$\mathcal{S}:=\{C\in\Gamma X:(r+s)\odot C=(r\odot C)\oplus (s\odot C)\}$
. By the preceding argument,
![]() $\{{\downarrow}x:x\in X\}\subseteq\mathcal{S}$
. For any directed family
$\{{\downarrow}x:x\in X\}\subseteq\mathcal{S}$
. For any directed family
![]() $\{A_i:i\in I\}$
of
$\{A_i:i\in I\}$
of
![]() $\mathcal{S}$
,
$\mathcal{S}$
,

It is easy to see that
It follows that
![]() $\bigvee_{i\in I}A_i\in\mathcal{S}$
. Hence, we have
$\bigvee_{i\in I}A_i\in\mathcal{S}$
. Hence, we have
![]() $A\in\tilde{X}\subseteq\mathcal{S}$
.
$A\in\tilde{X}\subseteq\mathcal{S}$
.
Finally, for any fixed
![]() $A\in\tilde{X}, g=\lambda x.x\odot A\colon\mathbb{R^+}\rightarrow\tilde{X}$
is Scott continuous. Since
$A\in\tilde{X}, g=\lambda x.x\odot A\colon\mathbb{R^+}\rightarrow\tilde{X}$
is Scott continuous. Since
![]() $\lambda x.xa\colon \mathbb{R^+}\rightarrow X$
is continuous for each
$\lambda x.xa\colon \mathbb{R^+}\rightarrow X$
is continuous for each
![]() $a\in X$
, then g is monotone. Given any bounded directed set
$a\in X$
, then g is monotone. Given any bounded directed set
![]() $\{x_i:i\in I\}\subseteq\mathbb{R^+}$
,
$\{x_i:i\in I\}\subseteq\mathbb{R^+}$
,
![]() $(\bigvee_{i\in I}^{\uparrow}x_i)\odot A=\{(\bigvee_{i\in I}^{\uparrow}x_i)a:a\in A\}=\{\bigvee_{i\in I}^{\uparrow}x_ia:a\in A\}\subseteq \overline{\bigcup_{i\in I}^{\uparrow}x_i\odot A}=\bigvee_{i\in I}^{\uparrow}(x_i\odot A)$
. It is easily seen that
$(\bigvee_{i\in I}^{\uparrow}x_i)\odot A=\{(\bigvee_{i\in I}^{\uparrow}x_i)a:a\in A\}=\{\bigvee_{i\in I}^{\uparrow}x_ia:a\in A\}\subseteq \overline{\bigcup_{i\in I}^{\uparrow}x_i\odot A}=\bigvee_{i\in I}^{\uparrow}(x_i\odot A)$
. It is easily seen that
![]() $\bigvee_{i\in I}^{\uparrow}(x_i\odot A)\subseteq(\bigvee_{i\in I}^{\uparrow}x_i)\odot A$
. We conclude that
$\bigvee_{i\in I}^{\uparrow}(x_i\odot A)\subseteq(\bigvee_{i\in I}^{\uparrow}x_i)\odot A$
. We conclude that
![]() $\bigvee_{i\in I}^{\uparrow}(x_i\odot A)=(\bigvee_{i\in I}^{\uparrow}x_i)\odot A$
. Therefore
$\bigvee_{i\in I}^{\uparrow}(x_i\odot A)=(\bigvee_{i\in I}^{\uparrow}x_i)\odot A$
. Therefore
![]() $(\tilde{X},\oplus,\odot)$
is a dcpo-cone.
$(\tilde{X},\oplus,\odot)$
is a dcpo-cone.
Next we give the construction of free dcpo-cone over any dcpo by using the D-completions. It is one of the main results of this paper.
Theorem 36. Let D be a dcpo. The standard Scott completion
![]() $\big( (\mathfrak{D},\oplus,\odot),i\big)$
of
$\big( (\mathfrak{D},\oplus,\odot),i\big)$
of
![]() $P_D(\Sigma D)$
is the free dcpo-cone, that is, given any dcpo-cone
$P_D(\Sigma D)$
is the free dcpo-cone, that is, given any dcpo-cone
![]() $\mathfrak{E}$
and any Scott continuous map
$\mathfrak{E}$
and any Scott continuous map
![]() $f\colon D\rightarrow\mathfrak{E}$
, if we assign
$f\colon D\rightarrow\mathfrak{E}$
, if we assign
![]() $\xi=i\circ\eta'\colon D\rightarrow$
$\xi=i\circ\eta'\colon D\rightarrow$
![]() $\mathfrak{D}$
, where
$\mathfrak{D}$
, where
![]() $\forall d\in D:$
$\forall d\in D:$
![]() $\eta'(d)=\eta_{d}$
. Then, there is a unique Scott continuous linear map
$\eta'(d)=\eta_{d}$
. Then, there is a unique Scott continuous linear map
![]() $\bar{f}\colon\mathfrak{D}\rightarrow\mathfrak{E}$
such that
$\bar{f}\colon\mathfrak{D}\rightarrow\mathfrak{E}$
such that
![]() $\bar{f}\circ\xi=f$
.
$\bar{f}\circ\xi=f$
.

Proof. Since
![]() $\mathfrak{E}$
is a dcpo-cone, it is also a monotone determined cone with respect to Scott topology. Because
$\mathfrak{E}$
is a dcpo-cone, it is also a monotone determined cone with respect to Scott topology. Because
![]() $P_D(\Sigma D)$
is the free monotone determined cone over
$P_D(\Sigma D)$
is the free monotone determined cone over
![]() $\Sigma D$
, there exists a unique continuous linear map
$\Sigma D$
, there exists a unique continuous linear map
![]() $\hat{f}\colon P_D(\Sigma D)\rightarrow \mathfrak{E}$
such that
$\hat{f}\colon P_D(\Sigma D)\rightarrow \mathfrak{E}$
such that
![]() $\hat{f}\circ\eta'=f$
. By a similar argument, there is a unique continuous map
$\hat{f}\circ\eta'=f$
. By a similar argument, there is a unique continuous map
![]() $\bar{f}\colon\mathfrak{D}\rightarrow \mathfrak{E}$
with
$\bar{f}\colon\mathfrak{D}\rightarrow \mathfrak{E}$
with
![]() $\bar{f}\circ i=\hat{f}$
. We claim that
$\bar{f}\circ i=\hat{f}$
. We claim that
![]() $\bar{f}$
is also a linear map between
$\bar{f}$
is also a linear map between
![]() $\mathfrak{D}$
and
$\mathfrak{D}$
and
![]() $\mathfrak{E}$
. For any element
$\mathfrak{E}$
. For any element
![]() $F\in\mathfrak{D}$
,
$F\in\mathfrak{D}$
,
![]() $\bar{f}(F)=\bigvee\overline{\hat{f}(F)}$
. Given any
$\bar{f}(F)=\bigvee\overline{\hat{f}(F)}$
. Given any
![]() $\lambda\in\mathbb{R^+}$
,
$\lambda\in\mathbb{R^+}$
,
![]() $\bar{f}(\lambda\odot F)=\bigvee\overline{\hat{f}(\lambda\odot F)}=\bigvee\overline{\lambda\odot\hat{f}(F)}=\bigvee(\lambda\overline{\hat{f}(F)})=\lambda\cdot\bigvee(\overline{\hat{f}(F)})=\lambda\cdot\bar{f}(F)$
. For any
$\bar{f}(\lambda\odot F)=\bigvee\overline{\hat{f}(\lambda\odot F)}=\bigvee\overline{\lambda\odot\hat{f}(F)}=\bigvee(\lambda\overline{\hat{f}(F)})=\lambda\cdot\bigvee(\overline{\hat{f}(F)})=\lambda\cdot\bar{f}(F)$
. For any
![]() $A,B\in\mathcal{F}$
, we calculate
$A,B\in\mathcal{F}$
, we calculate

Suppose that there is another Scott continuous linear map
![]() $g\colon\mathfrak{D}\rightarrow\mathfrak{E}$
such that
$g\colon\mathfrak{D}\rightarrow\mathfrak{E}$
such that
![]() $g\circ\xi=f$
. Set
$g\circ\xi=f$
. Set
![]() $S=\{x\in\mathfrak{D}:\bar{f}(x)=g(x)\}$
. Clearly, S is closed under addition and scalar multiplication. Because
$S=\{x\in\mathfrak{D}:\bar{f}(x)=g(x)\}$
. Clearly, S is closed under addition and scalar multiplication. Because
![]() $\bar{f}$
and g are Scott continuous, S is also a sub-dcpo of
$\bar{f}$
and g are Scott continuous, S is also a sub-dcpo of
![]() $\mathfrak{D}$
. It is easy to see that for any
$\mathfrak{D}$
. It is easy to see that for any
![]() $d\in D$
,
$d\in D$
,
![]() $\xi(d)\in S$
. Since i preserves multiplication,
$\xi(d)\in S$
. Since i preserves multiplication,
![]() $i(r\cdot\eta_{d})=r\odot (i\circ\eta'(d))=r\odot\xi(d)\in S$
. By the additivity of i,
$i(r\cdot\eta_{d})=r\odot (i\circ\eta'(d))=r\odot\xi(d)\in S$
. By the additivity of i,
![]() $i(a)\in S$
for any
$i(a)\in S$
for any
![]() $a\in P_D(\Sigma D)$
. Hence, S is equal to
$a\in P_D(\Sigma D)$
. Hence, S is equal to
![]() $\mathfrak{D}$
because the image of i is d-dense in
$\mathfrak{D}$
because the image of i is d-dense in
![]() $\mathfrak{D}$
. Consequently
$\mathfrak{D}$
. Consequently
![]() $\bar{f}=g$
.
$\bar{f}=g$
.
Remark 37. By the above argument, we have actually shown that the standard Scott-completion functor
![]() $\colon \textbf{Dscone}\rightarrow\textbf{Dcone}$
is the left adjoint of the forgetful functor. Jia and Mislove (Reference Jia and Mislove2022) have considered the D-completion of
$\colon \textbf{Dscone}\rightarrow\textbf{Dcone}$
is the left adjoint of the forgetful functor. Jia and Mislove (Reference Jia and Mislove2022) have considered the D-completion of
![]() $\mathcal{V}_f(X)$
with the weak topology and dcpo completion of the poset
$\mathcal{V}_f(X)$
with the weak topology and dcpo completion of the poset
![]() $\mathcal{V}_{f}(X)$
, which are different from our construction due to the different topology on
$\mathcal{V}_{f}(X)$
, which are different from our construction due to the different topology on
![]() $\mathcal{V}_{f}(X)$
.
$\mathcal{V}_{f}(X)$
.
5. Valuation Power domain and Free dcpo-cone
A well-known result in probabilistic power domain theory is that the space of continuous valuations over
![]() $\Sigma D$
is the free dcpo-cone of
$\Sigma D$
is the free dcpo-cone of
![]() $\Sigma D$
if D is a continuous domain (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorem IV-9.24). But it is unknown whether this result still holds for the case of general dcpos. In this section, we will discuss this problem and build some relationships between the space of valuations and the free dcpo-cones for more general dcpos instead of continuous ones.
$\Sigma D$
if D is a continuous domain (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorem IV-9.24). But it is unknown whether this result still holds for the case of general dcpos. In this section, we will discuss this problem and build some relationships between the space of valuations and the free dcpo-cones for more general dcpos instead of continuous ones.
In the following, we introduce some notations. Let F(D) denote the free dcpo-cone over D if D is a dcpo. For a topological space X, the valuation power domain (also called the extended probabilistic power domain)
![]() $\mathcal{V}(X)$
of X is the set of all continuous valuations on
$\mathcal{V}(X)$
of X is the set of all continuous valuations on
![]() $\mathcal{O}(X)$
with the pointwise order, sometimes called the stochastic order:
$\mathcal{O}(X)$
with the pointwise order, sometimes called the stochastic order:
![]() $\mu\leq\nu$
iff
$\mu\leq\nu$
iff
![]() $\mu(U)\leq\nu(U)$
for all open sets U.
$\mu(U)\leq\nu(U)$
for all open sets U.
Theorem 38. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorem IV-9.24) Given any dcpo-cone C and a continuous map
![]() $f:X\rightarrow C$
, where X is a domain equipped with the Scott topology, there exists a unique continuous linear map
$f:X\rightarrow C$
, where X is a domain equipped with the Scott topology, there exists a unique continuous linear map
![]() $f^{\ast}:\mathcal{V}(X)\rightarrow C$
such that
$f^{\ast}:\mathcal{V}(X)\rightarrow C$
such that
![]() $f^{\ast}\eta_X=f$
, here
$f^{\ast}\eta_X=f$
, here
![]() $\eta_X(x)=\eta_x,\ \forall x\in X$
.
$\eta_X(x)=\eta_x,\ \forall x\in X$
.
Let D be a domain. The extension map
![]() $\hat{\eta}\colon P_D(\Sigma D)\rightarrow\mathcal{V}(D)$
is a D-completion map. The topology on
$\hat{\eta}\colon P_D(\Sigma D)\rightarrow\mathcal{V}(D)$
is a D-completion map. The topology on
![]() $P_D(\Sigma D)$
is the subspace topology induced by the Scott topology on
$P_D(\Sigma D)$
is the subspace topology induced by the Scott topology on
![]() $\mathcal{V}(D)$
.
$\mathcal{V}(D)$
.
Proof. By Theorem 38
![]() $(\mathcal{V}(D),\eta)$
is the free dcpo-cone over continuous dcpo D. Applying Theorem 36 to this case, the map
$(\mathcal{V}(D),\eta)$
is the free dcpo-cone over continuous dcpo D. Applying Theorem 36 to this case, the map
![]() $\bar{\eta}\colon\mathcal{D}\rightarrow\mathcal{V}(D)$
is an isomorphism between d-cones.
$\bar{\eta}\colon\mathcal{D}\rightarrow\mathcal{V}(D)$
is an isomorphism between d-cones.

Clearly, the map
![]() $\bar{\eta}\colon \Sigma(\mathcal{D})\rightarrow\Sigma(\mathcal{V}(D))$
is also a topological isomorphism. Notice that
$\bar{\eta}\colon \Sigma(\mathcal{D})\rightarrow\Sigma(\mathcal{V}(D))$
is also a topological isomorphism. Notice that
![]() $i\colon P_D(\Sigma D)\rightarrow\mathcal{D}$
is a D-completion map. It follows that
$i\colon P_D(\Sigma D)\rightarrow\mathcal{D}$
is a D-completion map. It follows that
![]() $\hat{\eta}\colon P_D(\Sigma D)\rightarrow\mathcal{V}(D)$
is a D-completion map. Hence, the topology of
$\hat{\eta}\colon P_D(\Sigma D)\rightarrow\mathcal{V}(D)$
is a D-completion map. Hence, the topology of
![]() $P_D(\Sigma D)$
is the subspace topology induced by the Scott topology on
$P_D(\Sigma D)$
is the subspace topology induced by the Scott topology on
![]() $\mathcal{V}(D)$
.
$\mathcal{V}(D)$
.
Corollary 40. Let X be a c-space. The powerspace
![]() $P_D(X)$
is also a c-space.
$P_D(X)$
is also a c-space.
Proof.
![]() $X^{d}$
is a c-space by Propositions 6 and 26. Hence,
$X^{d}$
is a c-space by Propositions 6 and 26. Hence,
![]() $X^{d}$
with specialization order is a domain. Using the universal properties of D-completion on monotone determined spaces and
$X^{d}$
with specialization order is a domain. Using the universal properties of D-completion on monotone determined spaces and
![]() $\mathcal{V}$
on domains,
$\mathcal{V}$
on domains,
![]() $\mathcal{V}(X^d)$
is the free dcpo-cone over X. Similar arguments tell us that
$\mathcal{V}(X^d)$
is the free dcpo-cone over X. Similar arguments tell us that
![]() $P_D^{d}(X)$
is also the free dcpo-cone over X. Since
$P_D^{d}(X)$
is also the free dcpo-cone over X. Since
![]() $\mathcal{V}(X^d)$
is a continuous dcpo, then
$\mathcal{V}(X^d)$
is a continuous dcpo, then
![]() $P_D^{d}(X)\cong\mathcal{V}(X^d)$
is a c-space. Again by Propositions 6 and 26, we have that
$P_D^{d}(X)\cong\mathcal{V}(X^d)$
is a c-space. Again by Propositions 6 and 26, we have that
![]() $P_D(X)$
is also a c-space.
$P_D(X)$
is also a c-space.
Proposition 41. Let X be a topological space.
![]() $\mathcal{V}_{p}(X)$
(the set of point-continuous valuations, see Definition 8) with the usual addition and scalar multiplication is a dcpo-cone.
$\mathcal{V}_{p}(X)$
(the set of point-continuous valuations, see Definition 8) with the usual addition and scalar multiplication is a dcpo-cone.
Proof. It is easy to see that
![]() $\mathcal{V}_{p}(X)$
is a dcpo with the pointwise order and the supremum of a directed family
$\mathcal{V}_{p}(X)$
is a dcpo with the pointwise order and the supremum of a directed family
![]() $\{\mu_i:i\in I\}$
of point-continuous valuations is
$\{\mu_i:i\in I\}$
of point-continuous valuations is
![]() $\mu=\lambda U.\bigvee_{i\in I}^{\uparrow}\mu_i(U)$
for any
$\mu=\lambda U.\bigvee_{i\in I}^{\uparrow}\mu_i(U)$
for any
![]() $U\in\mathcal{O}(X)$
.
$U\in\mathcal{O}(X)$
.
We first show that
![]() $\mathcal{V}_{p}(X)$
is closed under addition. Given any two point-continuous valuations
$\mathcal{V}_{p}(X)$
is closed under addition. Given any two point-continuous valuations
![]() $\mu_1,\mu_2$
, for any
$\mu_1,\mu_2$
, for any
![]() $r\in \bar{\mathbb{R}}^{+}$
and
$r\in \bar{\mathbb{R}}^{+}$
and
![]() $U\in\mathcal{O}(X)$
, assume that
$U\in\mathcal{O}(X)$
, assume that
![]() $\mu_1(U)+\mu_2(U)>r$
. If one of
$\mu_1(U)+\mu_2(U)>r$
. If one of
![]() $\mu_1(U)$
and
$\mu_1(U)$
and
![]() $\mu_2(U)$
is equal to 0, without loss of generality we say
$\mu_2(U)$
is equal to 0, without loss of generality we say
![]() $\mu_1(U)=0$
, then
$\mu_1(U)=0$
, then
![]() $\mu_2(U)>r$
. Since
$\mu_2(U)>r$
. Since
![]() $\mu$
is point-continuous, there is a finite subset F of U such that
$\mu$
is point-continuous, there is a finite subset F of U such that
![]() $\mu_2(V)>r$
for any open set
$\mu_2(V)>r$
for any open set
![]() $V\supseteq F$
. It follows that
$V\supseteq F$
. It follows that
![]() $\mu_1(V)+\mu_2(V)>r$
for any open set
$\mu_1(V)+\mu_2(V)>r$
for any open set
![]() $V\supseteq F$
. Another case is that neither of
$V\supseteq F$
. Another case is that neither of
![]() $\mu_1(U)$
nor
$\mu_1(U)$
nor
![]() $\mu_2(U)$
is equal to 0. Take a positive real number
$\mu_2(U)$
is equal to 0. Take a positive real number
![]() $\epsilon$
such that
$\epsilon$
such that
![]() $\epsilon<\mu_1(U), \epsilon<\mu_2(U), \mu_1(U)-\epsilon+\mu_2(U)-\epsilon>r$
. By the point continuity of
$\epsilon<\mu_1(U), \epsilon<\mu_2(U), \mu_1(U)-\epsilon+\mu_2(U)-\epsilon>r$
. By the point continuity of
![]() $\mu_i$
(i=1,2), there is a finite set
$\mu_i$
(i=1,2), there is a finite set
![]() $F_i\subseteq U$
satisfying
$F_i\subseteq U$
satisfying
![]() $\mu_i(V)>\mu_i(U)-\epsilon$
for any open set
$\mu_i(V)>\mu_i(U)-\epsilon$
for any open set
![]() $V\supseteq F_i$
. Let F be the union of
$V\supseteq F_i$
. Let F be the union of
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, clearly
$F_2$
, clearly
![]() $\mu_1(V)+\mu_2(V)>r$
for any open set
$\mu_1(V)+\mu_2(V)>r$
for any open set
![]() $V\supseteq F$
. We conclude that
$V\supseteq F$
. We conclude that
![]() $\mu_1+\mu_2\in\mathcal{V}_{p}(X)$
.
$\mu_1+\mu_2\in\mathcal{V}_{p}(X)$
.
It is easily seen that
![]() $\mathcal{V}_{p}(X)$
is closed under scalar multiplication. It is a routine to check that
$\mathcal{V}_{p}(X)$
is closed under scalar multiplication. It is a routine to check that
![]() $\cdot\colon\mathbb{R}^{+}\times\mathcal{V}_{p}(X)\rightarrow\mathcal{V}_{p}(X)$
and
$\cdot\colon\mathbb{R}^{+}\times\mathcal{V}_{p}(X)\rightarrow\mathcal{V}_{p}(X)$
and
![]() $+\colon\mathcal{V}_{p}(X)\times\mathcal{V}_{p}(X)\rightarrow\mathcal{V}_{p}(X)$
are Scott continuous. Hence,
$+\colon\mathcal{V}_{p}(X)\times\mathcal{V}_{p}(X)\rightarrow\mathcal{V}_{p}(X)$
are Scott continuous. Hence,
![]() $\mathcal{V}_{p}(X)$
is a dcpo-cone.
$\mathcal{V}_{p}(X)$
is a dcpo-cone.
Example 42. Let D be the Smyth power domain (
![]() $\mathcal{Q}(\mathbb{R}_{\ell}))$
of the Sorgenfrey line
$\mathcal{Q}(\mathbb{R}_{\ell}))$
of the Sorgenfrey line
![]() $\mathbb{R}_{\ell}$
. By the result of Goubault and Jia (Reference Goubault-Larrecq and Jia2021, Theorem 39), the inclusion map
$\mathbb{R}_{\ell}$
. By the result of Goubault and Jia (Reference Goubault-Larrecq and Jia2021, Theorem 39), the inclusion map
![]() $j\colon\mathcal{V}_{p}(D)\rightarrow\mathcal{V}(D)$
is not surjective. We claim that
$j\colon\mathcal{V}_{p}(D)\rightarrow\mathcal{V}(D)$
is not surjective. We claim that
![]() $(\mathcal{V}(D),\eta)$
is not the free dcpo-cone over D. Let
$(\mathcal{V}(D),\eta)$
is not the free dcpo-cone over D. Let
![]() $(F(D),\xi)$
be the free dcpo-cone over D and
$(F(D),\xi)$
be the free dcpo-cone over D and
![]() $\eta_1$
the co-restriction of
$\eta_1$
the co-restriction of
![]() $\eta\colon D\rightarrow\mathcal{V}(D)$
on
$\eta\colon D\rightarrow\mathcal{V}(D)$
on
![]() $\mathcal{V}_{p}(D)$
. Obviously
$\mathcal{V}_{p}(D)$
. Obviously
![]() $\eta=j\circ\eta_1$
. By the universal property of F(D), there is a unique Scott continuous linear map f with
$\eta=j\circ\eta_1$
. By the universal property of F(D), there is a unique Scott continuous linear map f with
![]() $\eta_{1}=f\circ\xi$
. Let g denote the map
$\eta_{1}=f\circ\xi$
. Let g denote the map
![]() $j\circ f$
, then
$j\circ f$
, then
![]() $g\circ\xi=(j\circ f)\circ\xi=j\circ(f\circ\xi)=j\circ\eta_1=\eta$
. Clearly g is a Scott continuous linear map but not surjective. Hence,
$g\circ\xi=(j\circ f)\circ\xi=j\circ(f\circ\xi)=j\circ\eta_1=\eta$
. Clearly g is a Scott continuous linear map but not surjective. Hence,
![]() $(\mathcal{V}(D),\eta)$
is not a free dcpo-cone over D.
$(\mathcal{V}(D),\eta)$
is not a free dcpo-cone over D.

Remark 43. In the future, we plan to discuss the relations between the free dcpo-cone over a general (quasicontinuous) dcpo D and the space of minimal valuations over D (Goubault and Jia Reference Goubault-Larrecq and Jia2021).
Acknowledgements
We thank the anonymous referee for improving the presentation of the paper, and we would like to thank Chen Yu for patient and helpful discussions. This work was supported by NSF of China (Nos. 12001385, 12231007, 11871353) and “the Fundamental Research Funds for the Central Universities” No. 2021SCU12108.