Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T01:22:09.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Complete algebraic semantics for second-order rewriting systems based on abstract syntax with variable binding

Published online by Cambridge University Press:  14 October 2022

Makoto Hamana Open the ORCID record for Makoto Hamana [Opens in a new window]
Makoto Hamana*
Affiliation:
Faculty of Informatics, Gunma University, Maebashi, Japan
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

By using algebraic structures in a presheaf category over finite sets, following Fiore, Plotkin and Turi, we develop sound and complete models of second-order rewriting systems called second-order computation systems (CSs). Restricting the algebraic structures to those equipped with well-founded relations, we obtain a complete characterisation of terminating CSs. We also extend the characterisation to rewriting on meta-terms using the notion of 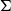$\Sigma$ -monoid.

Keywords

Term rewritinghigher-order rewritingterminationalgebraic modelshigher-order abstract syntax
Type
Special Issue: The Power Festschrift
Information
Mathematical Structures in Computer Science , Volume 32 , Special Issue 4: The Power Festschrift , April 2022 , pp. 542 - 573
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aczel, P. (1978). A General Church-Rosser Theorem. Technical report, University of Manchester.Google Scholar
Adamek, J. (1974). Free algebras and automata realizations in the language of categories. Commentationes Mathematicae Universitatis Carolinae 15 (589602).Google Scholar
Blanqui, F. (2000). Termination and confluence of higher-order rewrite systems. In: Rewriting Techniques and Application (RTA 2000), LNCS, vol. 1833. Springer, 47–61.CrossRefGoogle Scholar
Blanqui, F. (2016). Termination of rewrite relations on l-terms based on Girard’s notion of reducibility. Theoretical Computer Science 611 50–86.CrossRefGoogle Scholar
Blanqui, F., Jouannaud, J.-P. and Okada, M. (1999). The calculus of algebraic constructions. In: Rewriting Techniques and Applications (RTA 1999), LNCS, vol. 1631. Springer, 301–316.CrossRefGoogle Scholar
Blanqui, F., Jouannaud, J.-P. and Okada, M. (2002). Inductive data type systems. Theoretical Computer Science 272 41–68.CrossRefGoogle Scholar
Cohn, P. (1965). Universal Algebra. Harper & Row.Google Scholar
Danvy, O. and Rose, K. (1998). Higher-order rewriting and partial evaluation. In: Rewriting Techniques and Applications, 9th International Conference, (RTA’98), LNCS, vol. 1379.Google Scholar
de Bruijn, N. (1972). Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with application to the Church-Rosser theorem. Indagationes Mathematicae 34 381–391.CrossRefGoogle Scholar
Despeyroux, J., Felty, A. and Hirschowitz, A. (1995). Higher-order abstract syntax in Coq. In: Typed Lambda Calculi and Applications, LNCS, vol. 902, 124–138.CrossRefGoogle Scholar
Fiore, M. (2002). Semantic analysis of normalisation by evaluation for typed lambda calculus. In: 4th International Conference on Principles and Practice of Declarative Programming (PPDP 2002). ACM Press, 26–37.CrossRefGoogle Scholar
Fiore, M. (2008). Second-order and dependently-sorted abstract syntax. In: LICS’08, 57–68.CrossRefGoogle Scholar
Fiore, M. and Hamana, M. (2013). Multiversal polymorphic algebraic theories: Syntax, semantics, translations, and equational logic. In: 28th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS, vol. 2013, 520–529.CrossRefGoogle Scholar
Fiore, M. and Hur, C.-K. (2010). Second-order equational logic. In: CSL’10, LNCS, vol. 6247, 320–335.Google Scholar
Fiore, M. and Mahmoud, O. (2010). Second-order algebraic theories. In: MFCS’10, LNCS, vol. 6281, 368–380.CrossRefGoogle Scholar
Fiore, M., Plotkin, G. and Turi, D. (1999). Abstract syntax and variable binding. In: Proceedings of 14th Annual Symposium on Logic in Computer Science, 193–202.CrossRefGoogle Scholar
Gandy, R. (1980). Proofs of strong normalization. In: Seldin, J. P. and Hindley, J. R. (eds.) To H.B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism. Academic Press Limited.Google Scholar
Hamana, M. (2003). Term rewriting with variable binding: An initial algebra approach. In: Fifth ACM-SIGPLAN International Conference on Principles and Practice of Declarative Programming (PPDP’03), 148–159.CrossRefGoogle Scholar
Hamana, M. (2004). Free $\Sigma$ -monoids: A higher-order syntax with metavariables. In: Asian Symposium on Programming Languages and Systems (APLAS 2004), LNCS, vol. 3302, 348–363.Google Scholar
Hamana, M. (2005). Universal algebra for termination of higher-order rewriting. In: RTA’05, LNCS, vol. 3467, 135–149.CrossRefGoogle Scholar
Hamana, M. (2007). Higher-order semantic labelling for inductive datatype systems. In: PPDP’07, 97–108.CrossRefGoogle Scholar
Hamana, M. (2011). Polymorphic abstract syntax via Grothendieck construction. In FoSSaCS’11, LNCS, vol. 3467, 381–395.CrossRefGoogle Scholar
Hamana, M. (2017). How to prove your calculus is decidable: Practical applications of second-order algebraic theories and computation. Proceedings of the ACM on Programming Languages 1 (22) 1–28.CrossRefGoogle Scholar
Hamana, M. (2019). How to prove decidability of equational theories with second-order computation analyser SOL. Journal of Functional Programming 29 (e20).CrossRefGoogle Scholar
Hamana, M., Abe, T. and Kikuchi, K. (2020). Polymorphic computation systems: Theory and practice of confluence with call-by-value. Science of Computer Programming 187 (102322).CrossRefGoogle Scholar
Huet, G. and Lankford, D. S. (1978). On the uniform halting problem for term rewriting systems. Technical Report Rapport Laboria 283, INRIA.Google Scholar
Jouannaud, J.-P. and Rubio, A. (2001). Higher-order recursive path orderings à la carte. In: International Workshop on Rewriting in Proof and Computation (RPC’01), 161–175.Google Scholar
Klop, J. (1980). Combinatory Reduction Systems. PhD thesis, CWI, Amsterdam, vol. 127. Mathematical Centre Tracts.Google Scholar
Lescanne, P. and Rouyer-Degli, J. (1995). Explicit substitutions with de Bruijn’s levels. In: Rewriting Techniques and Applications, 6th International Conference (RTA-95), LNCS, vol. 914. Springer, 294–308.CrossRefGoogle Scholar
Libal, T. and Miller, D. (2016). Functions-as-constructors higher-order unification. In: Proceedings of FSCD 2016, vol. 52. LIPIcs, 26:1–26:17.Google Scholar
Mac Lane, S. (1971). Categories for the Working Mathematician, vol. 5. Graduate Texts in Mathematics. Springer-Verlag, New York.CrossRefGoogle Scholar
Mayr, R. and Nipkow, T. (1998). Higher-order rewrite systems and their confluence. Theoretical Computer Science 192 (1) 3–29.CrossRefGoogle Scholar
Miculan, M. and Scagnetto, I. (2003). A framework for typed HOAS and semantics. In: Proceedings of PPDP’03. ACM Press, 184–194.CrossRefGoogle Scholar
Miller, D. (1991). A logic programming language with lambda-abstraction, function variables, and simple unification. Journal of Logic and Computation 1 (4) 497–536.CrossRefGoogle Scholar
Milner, R. (1999). Communicating and Mobile Systems - The $\pi$ -Calculus. CUP.Google Scholar
Pfenning, F. and Elliott, C. (1988). Higher-order abstract syntax. In: Proceedings of the ACM SIGPLAN ’88 Symposium on Language Design and Implementation, 199–208.CrossRefGoogle Scholar
Plotkin, G. (1998). Binding algebras: A step between universal algebra and type theory (invited talk). In: Rewriting Techniques and Applications, 9th International Conference, RTA’98, Tsukuba, Japan.Google Scholar
Stark, I. (2008). Free-algebra models for the $\pi$ -calculus. Theoretical Computer Science 390 (2–3) 248–270.CrossRefGoogle Scholar
Tanaka, M. and Power, J. (2006). A unified category-theoretic semantics for binding signatures in substructural logics. Journal of Logic and Computation 16 (1) 5–25.CrossRefGoogle Scholar
Taylor, W. (1993). Abstract clone theory. Algebras and Orders 389 507–530. NATO ASI Series C.CrossRefGoogle Scholar
Turi, D. and Plotkin, G. (1997). Towards a mathematical operational semantics. In: Proceedings of the Twelfth Annual IEEE Symposium on Logic in Computer Science, LICS ’97, 280–291.CrossRefGoogle Scholar
van de Pol, J. (1994). Termination proofs for higher-order rewrite systems. In: The First International Workshop on Higher-Order Algebra, Logic and Term Rewriting (HOA’93), LNCS, vol. 816, 305–325.Google Scholar
van de Pol, J. (1996). Termination of Higher-order Rewrite Systems. PhD thesis, Universiteit Utrecht. https://cs.au.dk/jaco/papers/thesis.pdf Google Scholar
Yokoyama, T., Hu, Z. and Takeichi, M. (2003). Deterministic higher-order patterns for program transformation. In: Logic Based Program Synthesis and Transformation, 13th International Symposium LOPSTR 2003, Uppsala, Sweden, August 25–27, 2003, Revised Selected Papers, 128–142.Google Scholar
Yokoyama, T., Hu, Z. and Takeichi, M. (2004). Deterministic second-order patterns. Information Processing Letters 89 (6) 309–314.CrossRefGoogle Scholar
Zantema, H. (1994). Termination of term rewriting: Interpretation and type elimination. Journal of Symbolic Computation 17 23–50.CrossRefGoogle Scholar