Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T23:30:56.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Autostability spectra for decidable structures

Published online by Cambridge University Press:  14 October 2016

NIKOLAY BAZHENOV Open the ORCID record for NIKOLAY BAZHENOV [Opens in a new window]
NIKOLAY BAZHENOV*
Affiliation:
Sobolev Institute of Mathematics, Novosibirsk, Russia Novosibirsk State University, Novosibirsk, Russia Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

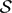We study autostability spectra relative to strong constructivizations (SC-autostability spectra). For a decidable structure $\mathcal{S}$, the SC-autostability spectrum of 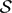$\mathcal{S}$ is the set of all Turing degrees capable of computing isomorphisms among arbitrary decidable copies of 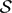$\mathcal{S}$. The degree of SC-autostability for 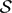$\mathcal{S}$ is the least degree in the spectrum (if such a degree exists).

We prove that for a computable successor ordinal α, every Turing degree c.e. in and above 0(α) is the degree of SC-autostability for some decidable structure. We show that for an infinite computable ordinal β, every Turing degree c.e. in and above 0(2β+1) is the degree of SC-autostability for some discrete linear order. We prove that the set of all PA-degrees is an SC-autostability spectrum. We also obtain similar results for autostability spectra relative to n-constructivizations.

Type
Paper
Information
Mathematical Structures in Computer Science , Volume 28 , Special Issue 3: Mind, Mechanism and Mathematics: Computability Unchained , March 2018 , pp. 392 - 411
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alaev, P.E. (2004). Hyperarithmetical Boolean algebras with a distinguished ideal. Siberian Mathematical Journal 45 (5) 795–805.Google Scholar
Anderson, B.A. and Csima, B.F. (2016). Degrees that are not degrees of categoricity. Notre Dame Journal of Formal Logic 57 (3) 389–398.Google Scholar
Ash, C.J. (1986a). Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees. Transactions of the American Mathematical Society 298 497–514.Google Scholar
Ash, C.J. (1986b). Stability of recursive structures in arithmetical degrees. Annals of Pure and Applied Logic 32 113–135.CrossRefGoogle Scholar
Ash, CJ. (1987). Categoricity in hyperarithmetical degrees. Annals of Pure and Applied Logic 34 (1) 1–14.Google Scholar
Ash, C.J. and Knight, J.F. (1990). Pairs of recursive structures. Annals of Pure and Applied Logic 46 (3) 211–234.Google Scholar
Ash, C.J. and Knight, J.F. (2000). Computable Structures and the Hyperarithmetical Hierarchy. Studies in Logic and the Foundations of Mathematics, volume 144, Elsevier Science B.V. Google Scholar
Ash, C., Knight, J., Manasse, M. and Slaman, T. (1989). Generic copies of countable structures. Annals of Pure and Applied Logic 42 (3) 195–205.Google Scholar
Bazhenov, N.A. (2013). Degrees of categoricity for superatomic Boolean algebras. Algebra Logic 52 (3) 179–187.Google Scholar
Bazhenov, N.A. (2014). Hyperarithmetical categoricity of Boolean algebras of type B(ωα × η). Journal of Mathematical Sciences 202 (1) 40–49.Google Scholar
Bazhenov, N.A. (2015a). Autostability spectra for Boolean algebras. Algebra Logic 53 (6) 502–505.Google Scholar
Bazhenov, N. (2015b). Prime model with no degree of autostability relative to strong constructivizations. In: Evolving Computability. Lecture Notes in Computer Science 9136, Springer, 117–126.Google Scholar
Bazhenov, N.A. (to appear). Degrees of autostability for linear orderings and linearly ordered abelian groups. Algebra Logic Google Scholar
Bazhenov, N.A. (2016). Degrees of autostability relative to strong constructivizations for Boolean algebras. Algebra Logic 55 (2) 87–102.Google Scholar
Chang, C.C. and Keisler, H.J. (1973). Model Theory. Elsevier, North-Holland.Google Scholar
Chisholm, J. (1990). Effective model theory vs. recursive model theory. The Journal of Symbolic Logic 55 (3) 1168–1191.Google Scholar
Chisholm, J., Fokina, E.B., Goncharov, S.S., Harizanov, V.S., Knight, J.F. and Quinn, S. (2009). Intrinsic bounds on complexity and definability at limit levels. The Journal of Symbolic Logic 74 (3) 1047–1060.Google Scholar
Csima, B.F., Franklin, J.N.Y. and Shore, R.A. (2013). Degrees of categoricity and the hyperarithmetic hierarchy. Notre Dame Journal of Formal Logic 54 (2) 215–231.Google Scholar
Downey, R.G. (1998). Computability theory and linear orderings. In: Ershov, Yu.L., Goncharov, S.S., Nerode, A. and Remmel, J.B. (eds.) Handbook of Recursive Mathematics 2 Studies in Logic and the Foundations of Mathematics, volume 139, Elsevier Science B.V, 823–976.Google Scholar
Downey, R.G., Kach, A.M., Lempp, S., Lewis-Pye, A.E.M., Montalbán, A. and Turetsky, D.D. (2015). The complexity of computable categoricity. Advances in Mathematics 268 423–466.Google Scholar
Ershov, Yu.L. (1964). Decidability of the elementary theory of distributive lattices with relative complements and the theory of filters. Algebra Logika 3 (3) 17–38.Google Scholar
Ershov, Yu.L. and Goncharov, S.S. (2000). Constructive Models. Kluwer Academic/Plenum Publishers.CrossRefGoogle Scholar
Fokina, E., Frolov, A. and Kalimullin, I. (2016). Categoricity spectra for rigid structures. Notre Dame Journal of Formal Logic 57 (1) 45–57.Google Scholar
Fokina, E.B., Goncharov, S.S., Harizanov, V., Kudinov, O.V. and Turetsky, D. (2015). Index sets for n-decidable structures categorical relative to m-decidable presentations. Algebra Logic 54 (4) 336–341.Google Scholar
Fokina, E.B., Kalimullin, I. and Miller, R. (2010). Degrees of categoricity of computable structures. Archive for Mathematical Logic 49 (1) 51–67.Google Scholar
Fröhlich, A. and Shepherdson, J.C. (1956). Effective procedures in field theory. Philosophical Transactions of the Royal Society of London A 248 (950) 407–432.Google Scholar
Frolov, A.N. (2012). Linear orderings. Coding theorems. Uchenye Zapiski Kazanskogo Universiteta, Seriya Fiziko-Matematicheskie Nauki. Kazan, 154 (2) 142–151. (In Russian).Google Scholar
Frolov, A.N. (2015). Effective categoricity of computable linear orderings. Algebra Logic 54 (5) 415–417.Google Scholar
Goncharov, S.S. (1977). The quantity of nonautoequivalent constructivizations. Algebra Logic 16 (3) 169–185.Google Scholar
Goncharov, S.S. (1997). Countable Boolean Algebras and Decidability. Consultants Bureau.Google Scholar
Goncharov, S.S. (2011). Degrees of autostability relative to strong constructivizations. Proceedings of the Steklov Institute of Mathematics 274 105–115.Google Scholar
Goncharov, S.S., Bazhenov, N.A. and Marchuk, M.I. (2015a). Index sets of autostable relative to strong constructivizations constructive models for familiar classes. Doklady Mathematics 92 (2) 525–527.Google Scholar
Goncharov, S.S., Bazhenov, N.A. and Marchuk, M.I. (2015b). The index set of Boolean algebras autostable relative to strong constructivizations. Siberian Mathematical Journal 56 (3) 393–404.CrossRefGoogle Scholar
Goncharov, S., Harizanov, V., Knight, J., McCoy, C., Miller, R. and Solomon, R. (2005). Enumerations in computable structure theory. Annals of Pure and Applied Logic 136 (3) 219–246.Google Scholar
Goncharov, S.S. and Marchuk, M.I. (2015a). Index sets of constructive models of bounded signature that are autostable relative to strong constructivizations. Algebra Logic 54 (2) 108–126.Google Scholar
Goncharov, S.S. and Marchuk, M.I. (2015b). Index sets of constructive models of nontrivial signature autostable relative to strong constructivizations. Doklady Mathematics 91 (2) 158–159.Google Scholar
Hirschfeldt, D.R., Khoussainov, B., Shore, R.A. and Slinko, A.M. (2002). Degree spectra and computable dimensions in algebraic structures. Annals of Pure and Applied Logic 115 (1–3) 71–113.CrossRefGoogle Scholar
Jockusch, C.G. and Soare, R.I. (1972). Π0 1 classes and degrees of theories. Transactions of the American Mathematical Society 173 33–56.Google Scholar
Langford, C.H. (1926). Some theorems on deducibility. Annals of Mathematics (2) 28 16–40.Google Scholar
Mal'tsev, A.I. (1961). Constructive algebras. I. Russian Mathematical Surveys 16 (3) 77–129.Google Scholar
Mal'tsev, A.I. (1962). On recursive abelian groups. Soviet Mathematics – Doklady 32 1431–1434.Google Scholar
Miller, R. (2009). d-computable categoricity for algebraic fields. Journal of Symbolic Logic 74 (4) 1325–1351.Google Scholar
Miller, R., Poonen, B., Schoutens, H. and Shlapentokh, A. (to appear). A computable functor from graphs to fields. arXiv:1510.07322Google Scholar
Miller, R. and Shlapentokh, A. (2015). Computable categoricity for algebraic fields with splitting algorithms. Transactions of the American Mathematical Society 367 (6) 3955–3980.Google Scholar
Moses, M. (1984). Recursive linear orders with recursive successivities. Annals of Pure and Applied Logic 27 (3) 253–264.CrossRefGoogle Scholar
Rosenstein, J.G. (1982). Linear Orderings. Pure and Applied Mathematics, volume 98, Academic Press.Google Scholar
Scott, D. (1962). Algebras of sets binumerable in complete extensions of arithmetic. In: Proceedings of Symposia in Pure Mathematics, volume V, American Mathematical Society 117–121.Google Scholar
Simpson, S.G. (1977). Degrees of unsolvability: A survey of results. In: Barwise, J. (ed.) Handbook of Mathematical Logic, Studies in Logic and the Foundations of Mathematics, volume 90, Elsevier, North-Holland 631–652.Google Scholar